Efficient Latent Variable Causal Discovery: Combining Score Search and Targeted Testing

Learning causal structure from observational data is especially challenging when latent variables or selection bias are present. The Fast Causal Inference (FCI) algorithm addresses this setting but often performs exhaustive conditional independence tests across many subsets, leading to spurious independence claims, extra or missing edges, and unreliable orientations. We present a family of score-guided mixed-strategy causal search algorithms that build on this tradition. First, we introduce BOSS-FCI and GRaSP-FCI, straightforward variants of GFCI that substitute BOSS or GRaSP for FGES, thereby retaining correctness while incurring different scalability tradeoffs. Second, we develop FCI Targeted-testing (FCIT), a novel mixed-strategy method that improves upon these variants by replacing exhaustive all-subsets testing with targeted tests guided by BOSS, yielding well-formed PAGs with higher precision and efficiency. Finally, we propose a simple heuristic, LV-Dumb (also known as BOSS-POD), which bypasses latent-variable-specific reasoning and directly returns the PAG of the BOSS DAG. Although not strictly correct in the FCI sense, it scales better and often achieves superior accuracy in practice. Simulations and real-data analyses demonstrate that BOSS-FCI and GRaSP-FCI provide sound baselines, FCIT improves both efficiency and reliability, and LV-Dumb offers a practical heuristic with strong empirical performance. Together, these method highlight the value of score-guided and targeted strategies for scalable latent-variable causal discovery.

Scalable Causal Discovery from Recursive Nonlinear Data via Truncated Basis Function Scores and Tests

Learning graphical conditional independence structures from nonlinear, continuous or mixed data is a central challenge in machine learning and the sciences, and many existing methods struggle to scale to thousands of samples or hundreds of variables. We introduce two basis-expansion tools for scalable causal discovery. First, the Basis Function BIC (BF-BIC) score uses truncated additive expansions to approximate nonlinear dependencies. BF-BIC is theoretically consistent under additive models and extends to post-nonlinear (PNL) models via an invertible reparameterization. It remains robust under moderate interactions and supports mixed data through a degenerate-Gaussian embedding for discrete variables. In simulations with fully nonlinear neural causal models (NCMs), BF-BIC outperforms kernel- and constraint-based methods (e.g., KCI, RFCI) in both accuracy and runtime. Second, the Basis Function Likelihood Ratio Test (BF-LRT) provides an approximate conditional independence test that is substantially faster than kernel tests while retaining competitive accuracy. Extensive simulations and a real-data application to Canadian wildfire risk show that, when integrated into hybrid searches, BF-based methods enable interpretable and scalable causal discovery. Implementations are available in Python, R, and Java.

An extensive simulation study evaluating the interaction of resampling techniques across multiple causal discovery contexts

Despite the accelerating presence of exploratory causal analysis in modern science and medicine, the available non-experimental methods for validating causal models are not well characterized. One of the most popular methods is to evaluate the stability of model features after resampling the data, similar to resampling methods for estimating confidence intervals in statistics. Many aspects of this approach have received little to no attention, however, such as whether the choice of resampling method should depend on the sample size, algorithms being used, or algorithm tuning parameters. We present theoretical results proving that certain resampling methods closely emulate the assignment of specific values to algorithm tuning parameters. We also report the results of extensive simulation experiments, which verify the theoretical result and provide substantial data to aid researchers in further characterizing resampling in the context of causal discovery analysis. Together, the theoretical work and simulation results provide specific guidance on how resampling methods and tuning parameters should be selected in practice.

Choosing DAG Models Using Markov and Minimal Edge Count in the Absence of Ground Truth

We give a novel nonparametric pointwise consistent statistical test (the Markov Checker) of the Markov condition for directed acyclic graph (DAG) or completed partially directed acyclic graph (CPDAG) models given a dataset. We also introduce the Cross-Algorithm Frugality Search (CAFS) for rejecting DAG models that either do not pass the Markov Checker test or that are not edge minimal. Edge minimality has been used previously by Raskutti and Uhler as a nonparametric simplicity criterion, though CAFS readily generalizes to other simplicity conditions. Reference to the ground truth is not necessary for CAFS, so it is useful for finding causal structure learning algorithms and tuning parameter settings that output causal models that are approximately true from a given data set. We provide a software tool for this analysis that is suitable for even quite large or dense models, provided a suitably fast pointwise consistent test of conditional independence is available. In addition, we show in simulation that the CAFS procedure can pick approximately correct models without knowing the ground truth.

Better Simulations for Validating Causal Discovery with the DAG-Adaptation of the Onion Method

The number of artificial intelligence algorithms for learning causal models from data is growing rapidly. Most ``causal discovery'' or ``causal structure learning'' algorithms are primarily validated through simulation studies. However, no widely accepted simulation standards exist and publications often report conflicting performance statistics -- even when only considering publications that simulate data from linear models. In response, several manuscripts have criticized a popular simulation design for validating algorithms in the linear case. We propose a new simulation design for generating linear models for directed acyclic graphs (DAGs): the DAG-adaptation of the Onion (DaO) method. DaO simulations are fundamentally different from existing simulations because they prioritize the distribution of correlation matrices rather than the distribution of linear effects. Specifically, the DaO method uniformly samples the space of all correlation matrices consistent with (i.e. Markov to) a DAG. We also discuss how to sample DAGs and present methods for generating DAGs with scale-free in-degree or out-degree. We compare the DaO method against two alternative simulation designs and provide implementations of the DaO method in Python and R: https://github.com/bja43/DaO_simulation. We advocate for others to adopt DaO simulations as a fair universal benchmark.

Causal Discovery for fMRI data: Challenges, Solutions, and a Case Study

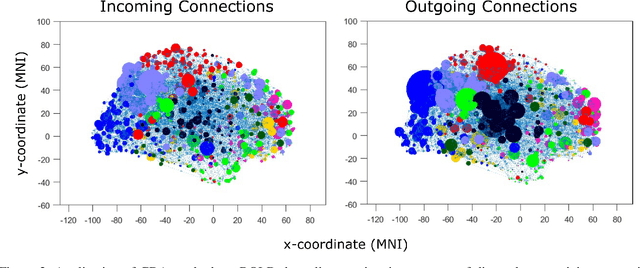
Designing studies that apply causal discovery requires navigating many researcher degrees of freedom. This complexity is exacerbated when the study involves fMRI data. In this paper we (i) describe nine challenges that occur when applying causal discovery to fMRI data, (ii) discuss the space of decisions that need to be made, (iii) review how a recent case study made those decisions, (iv) and identify existing gaps that could potentially be solved by the development of new methods. Overall, causal discovery is a promising approach for analyzing fMRI data, and multiple successful applications have indicated that it is superior to traditional fMRI functional connectivity methods, but current causal discovery methods for fMRI leave room for improvement.

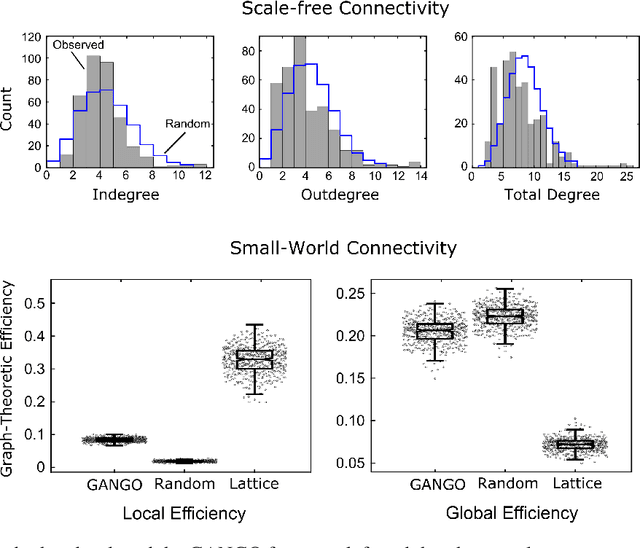
Fast Scalable and Accurate Discovery of DAGs Using the Best Order Score Search and Grow-Shrink Trees

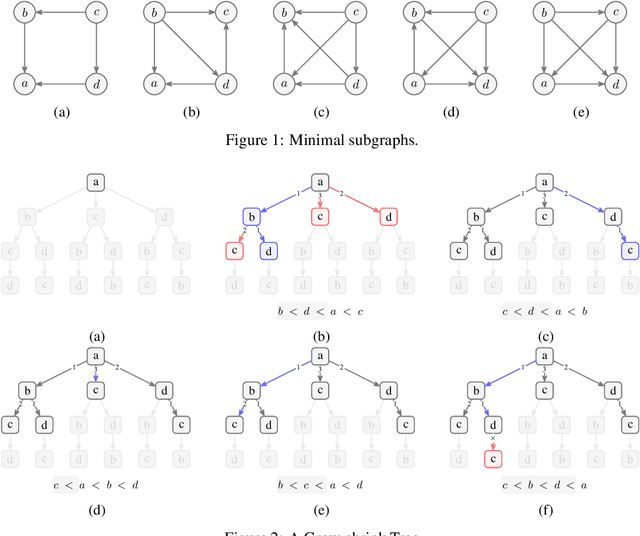
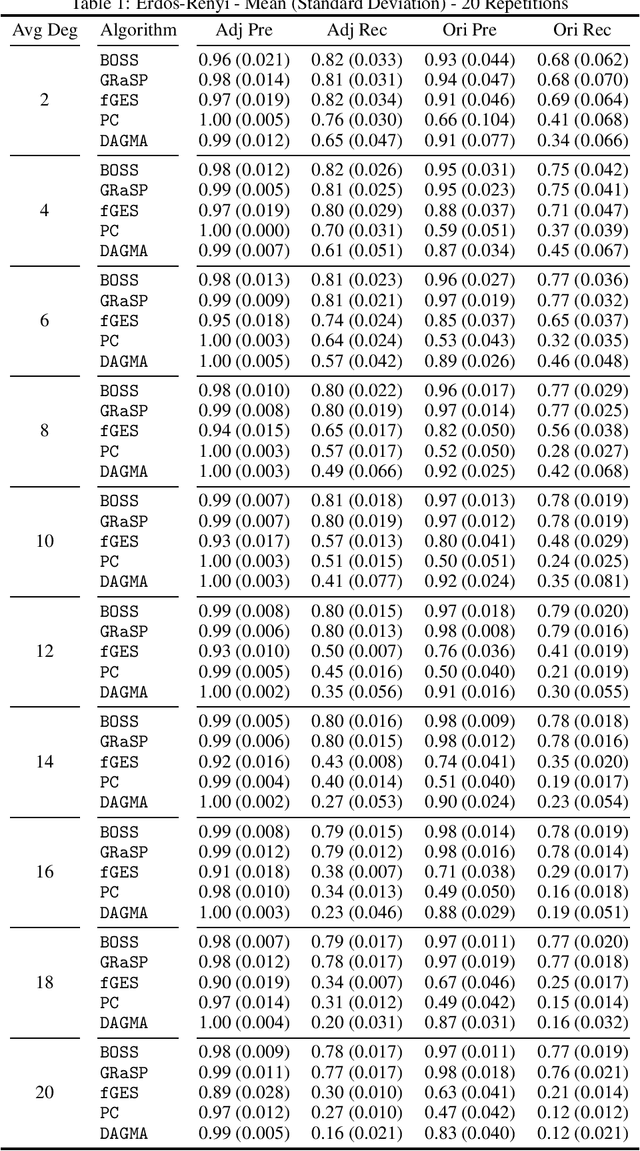
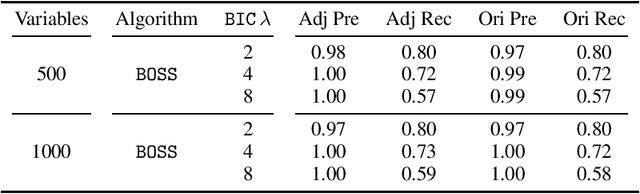
Learning graphical conditional independence structures is an important machine learning problem and a cornerstone of causal discovery. However, the accuracy and execution time of learning algorithms generally struggle to scale to problems with hundreds of highly connected variables -- for instance, recovering brain networks from fMRI data. We introduce the best order score search (BOSS) and grow-shrink trees (GSTs) for learning directed acyclic graphs (DAGs) in this paradigm. BOSS greedily searches over permutations of variables, using GSTs to construct and score DAGs from permutations. GSTs efficiently cache scores to eliminate redundant calculations. BOSS achieves state-of-the-art performance in accuracy and execution time, comparing favorably to a variety of combinatorial and gradient-based learning algorithms under a broad range of conditions. To demonstrate its practicality, we apply BOSS to two sets of resting-state fMRI data: simulated data with pseudo-empirical noise distributions derived from randomized empirical fMRI cortical signals and clinical data from 3T fMRI scans processed into cortical parcels. BOSS is available for use within the TETRAD project which includes Python and R wrappers.

Py-Tetrad and RPy-Tetrad: A New Python Interface with R Support for Tetrad Causal Search

We give novel Python and R interfaces for the (Java) Tetrad project for causal modeling, search, and estimation. The Tetrad project is a mainstay in the literature, having been under consistent development for over 30 years. Some of its algorithms are now classics, like PC and FCI; others are recent developments. It is increasingly the case, however, that researchers need to access the underlying Java code from Python or R. Existing methods for doing this are inadequate. We provide new, up-to-date methods using the JPype Python-Java interface and the Reticulate Python-R interface, directly solving these issues. With the addition of some simple tools and the provision of working examples for both Python and R, using JPype and Reticulate to interface Python and R with Tetrad is straightforward and intuitive.

The m-connecting imset and factorization for ADMG models

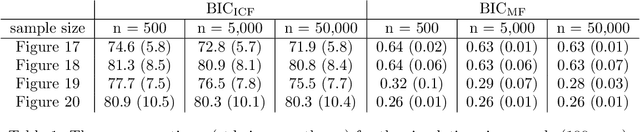
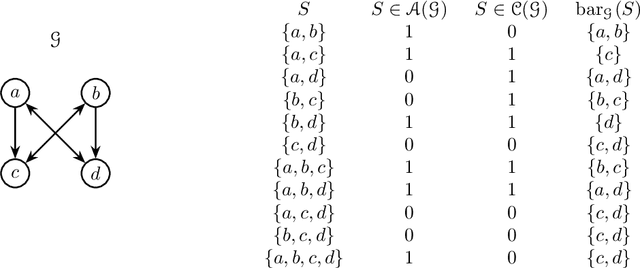
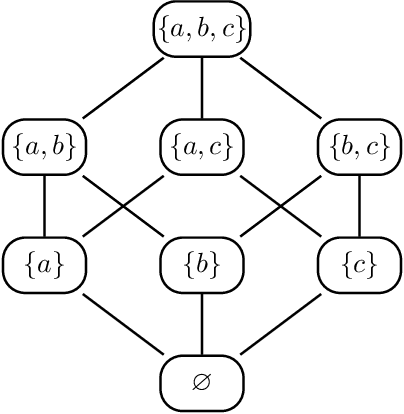
Directed acyclic graph (DAG) models have become widely studied and applied in statistics and machine learning -- indeed, their simplicity facilitates efficient procedures for learning and inference. Unfortunately, these models are not closed under marginalization, making them poorly equipped to handle systems with latent confounding. Acyclic directed mixed graph (ADMG) models characterize margins of DAG models, making them far better suited to handle such systems. However, ADMG models have not seen wide-spread use due to their complexity and a shortage of statistical tools for their analysis. In this paper, we introduce the m-connecting imset which provides an alternative representation for the independence models induced by ADMGs. Furthermore, we define the m-connecting factorization criterion for ADMG models, characterized by a single equation, and prove its equivalence to the global Markov property. The m-connecting imset and factorization criterion provide two new statistical tools for learning and inference with ADMG models. We demonstrate the usefulness of these tools by formulating and evaluating a consistent scoring criterion with a closed form solution.

Greedy Relaxations of the Sparsest Permutation Algorithm

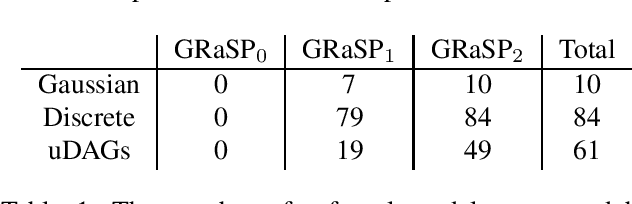
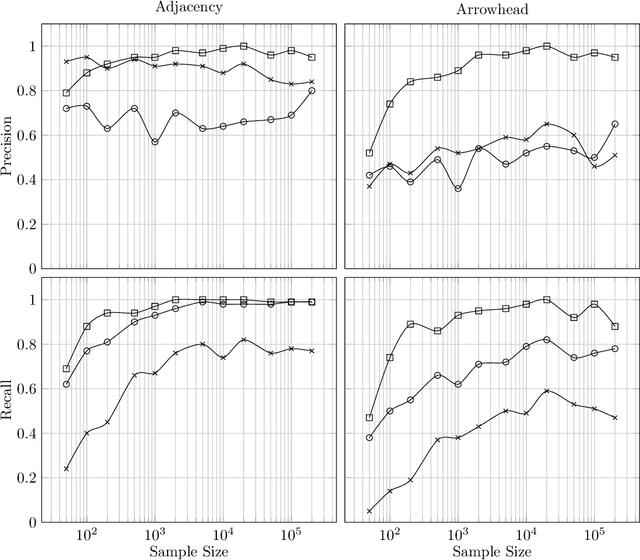
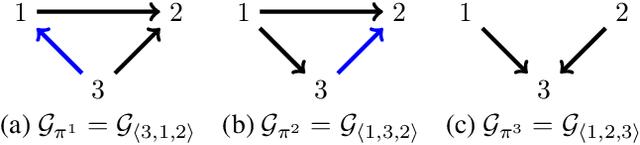
There has been an increasing interest in methods that exploit permutation reasoning to search for directed acyclic causal models, including the "Ordering Search" of Teyssier and Kohler and GSP of Solus, Wang and Uhler. We extend the methods of the latter by a permutation-based operation, tuck, and develop a class of algorithms, namely GRaSP, that are efficient and pointwise consistent under increasingly weaker assumptions than faithfulness. The most relaxed form of GRaSP outperforms many state-of-the-art causal search algorithms in simulation, allowing efficient and accurate search even for dense graphs and graphs with more than 100 variables.