Testing Identifiability and Transportability with Observational and Experimental Data

Transporting causal information learned from experiments in one population to another is a critical challenge in clinical research and decision-making. Causal transportability uses causal graphs to model differences between the source and target populations and identifies conditions under which causal effects learned from experiments can be reused in a different population. Similarly, causal identifiability identifies conditions under which causal effects can be estimated from observational data. However, these approaches rely on knowing the causal graph, which is often unavailable in real-world settings. In this work, we propose a Bayesian method for assessing whether Z-specific (conditional) causal effects are both identifiable and transportable, without knowing the causal graph. Our method combines experimental data from the source population with observational data from the target population to compute the probability that a causal effect is both identifiable from observational data and transportable. When this holds, we leverage both observational data from the target domain and experimental data from the source domain to obtain an unbiased, efficient estimator of the causal effect in the target population. Using simulations, we demonstrate that our method correctly identifies transportable causal effects and improves causal effect estimation.

Online Transfer Learning for RSV Case Detection

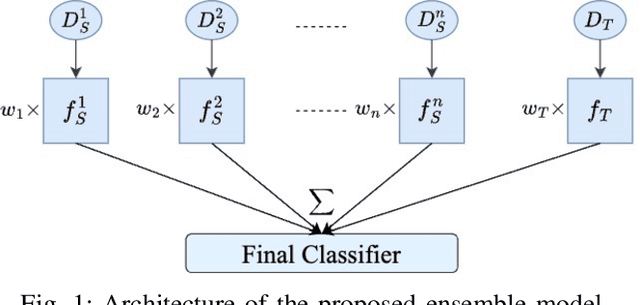
Transfer learning has become a pivotal technique in machine learning, renowned for its effectiveness in various real-world applications. However, a significant challenge arises when applying this approach to sequential epidemiological data, often characterized by a scarcity of labeled information. To address this challenge, we introduce Predictive Volume-Adaptive Weighting (PVAW), a novel online multi-source transfer learning method. PVAW innovatively implements a dynamic weighting mechanism within an ensemble model, allowing for the automatic adjustment of weights based on the relevance and contribution of each source and target model. We demonstrate the effectiveness of PVAW through its application in analyzing Respiratory Syncytial Virus (RSV) data, collected over multiple seasons at the University of Pittsburgh Medical Center. Our method showcases significant improvements in model performance over existing baselines, highlighting the potential of online transfer learning in handling complex, sequential data. This study not only underscores the adaptability and sophistication of transfer learning in healthcare but also sets a new direction for future research in creating advanced predictive models.

The m-connecting imset and factorization for ADMG models

Directed acyclic graph (DAG) models have become widely studied and applied in statistics and machine learning -- indeed, their simplicity facilitates efficient procedures for learning and inference. Unfortunately, these models are not closed under marginalization, making them poorly equipped to handle systems with latent confounding. Acyclic directed mixed graph (ADMG) models characterize margins of DAG models, making them far better suited to handle such systems. However, ADMG models have not seen wide-spread use due to their complexity and a shortage of statistical tools for their analysis. In this paper, we introduce the m-connecting imset which provides an alternative representation for the independence models induced by ADMGs. Furthermore, we define the m-connecting factorization criterion for ADMG models, characterized by a single equation, and prove its equivalence to the global Markov property. The m-connecting imset and factorization criterion provide two new statistical tools for learning and inference with ADMG models. We demonstrate the usefulness of these tools by formulating and evaluating a consistent scoring criterion with a closed form solution.

Learning Latent Causal Structures with a Redundant Input Neural Network

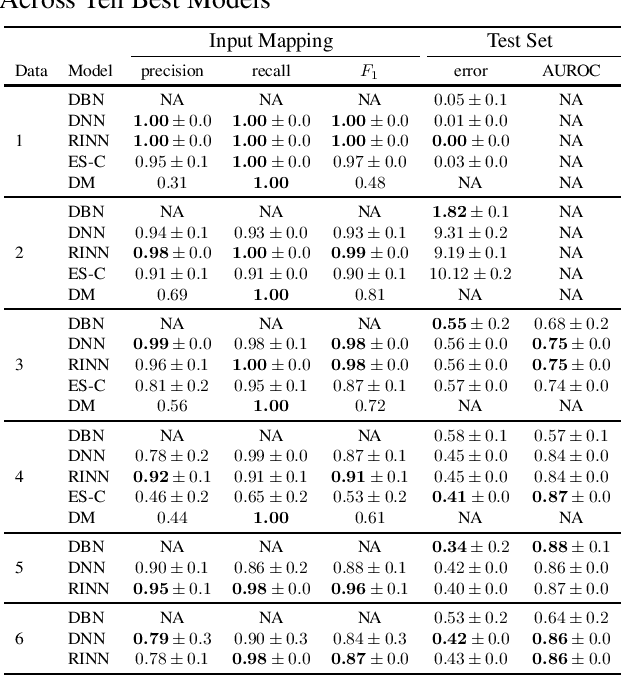
Most causal discovery algorithms find causal structure among a set of observed variables. Learning the causal structure among latent variables remains an important open problem, particularly when using high-dimensional data. In this paper, we address a problem for which it is known that inputs cause outputs, and these causal relationships are encoded by a causal network among a set of an unknown number of latent variables. We developed a deep learning model, which we call a redundant input neural network (RINN), with a modified architecture and a regularized objective function to find causal relationships between input, hidden, and output variables. More specifically, our model allows input variables to directly interact with all latent variables in a neural network to influence what information the latent variables should encode in order to generate the output variables accurately. In this setting, the direct connections between input and latent variables makes the latent variables partially interpretable; furthermore, the connectivity among the latent variables in the neural network serves to model their potential causal relationships to each other and to the output variables. A series of simulation experiments provide support that the RINN method can successfully recover latent causal structure between input and output variables.

Obtaining Accurate Probabilistic Causal Inference by Post-Processing Calibration

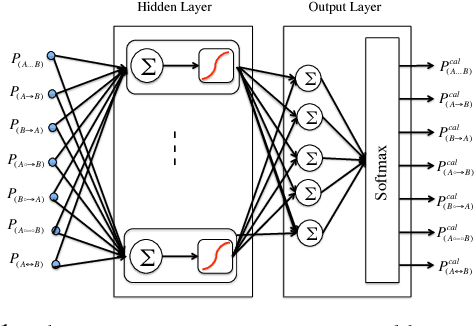
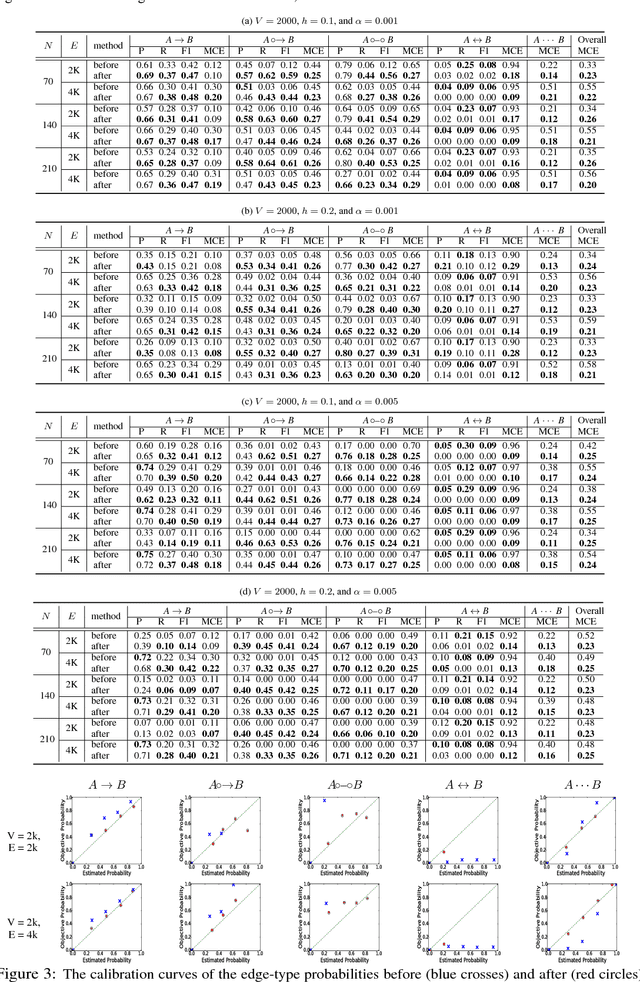
Discovery of an accurate causal Bayesian network structure from observational data can be useful in many areas of science. Often the discoveries are made under uncertainty, which can be expressed as probabilities. To guide the use of such discoveries, including directing further investigation, it is important that those probabilities be well-calibrated. In this paper, we introduce a novel framework to derive calibrated probabilities of causal relationships from observational data. The framework consists of three components: (1) an approximate method for generating initial probability estimates of the edge types for each pair of variables, (2) the availability of a relatively small number of the causal relationships in the network for which the truth status is known, which we call a calibration training set, and (3) a calibration method for using the approximate probability estimates and the calibration training set to generate calibrated probabilities for the many remaining pairs of variables. We also introduce a new calibration method based on a shallow neural network. Our experiments on simulated data support that the proposed approach improves the calibration of causal edge predictions. The results also support that the approach often improves the precision and recall of predictions.

Binary Classifier Calibration using an Ensemble of Near Isotonic Regression Models

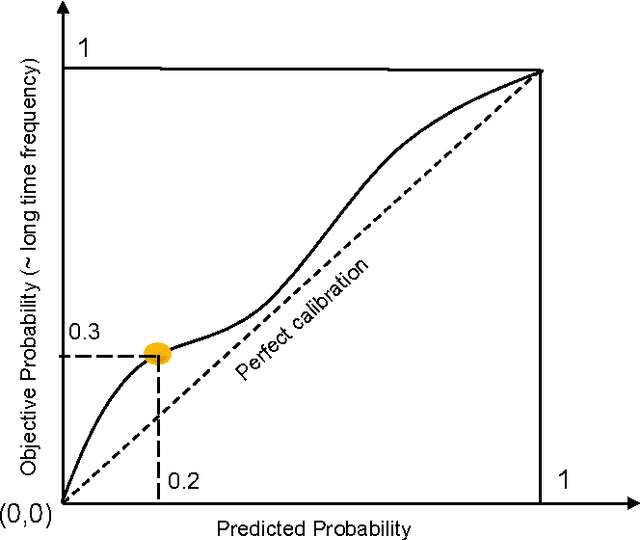
Learning accurate probabilistic models from data is crucial in many practical tasks in data mining. In this paper we present a new non-parametric calibration method called \textit{ensemble of near isotonic regression} (ENIR). The method can be considered as an extension of BBQ, a recently proposed calibration method, as well as the commonly used calibration method based on isotonic regression. ENIR is designed to address the key limitation of isotonic regression which is the monotonicity assumption of the predictions. Similar to BBQ, the method post-processes the output of a binary classifier to obtain calibrated probabilities. Thus it can be combined with many existing classification models. We demonstrate the performance of ENIR on synthetic and real datasets for the commonly used binary classification models. Experimental results show that the method outperforms several common binary classifier calibration methods. In particular on the real data, ENIR commonly performs statistically significantly better than the other methods, and never worse. It is able to improve the calibration power of classifiers, while retaining their discrimination power. The method is also computationally tractable for large scale datasets, as it is $O(N \log N)$ time, where $N$ is the number of samples.

Counting Markov Blanket Structures

Learning Markov blanket (MB) structures has proven useful in performing feature selection, learning Bayesian networks (BNs), and discovering causal relationships. We present a formula for efficiently determining the number of MB structures given a target variable and a set of other variables. As expected, the number of MB structures grows exponentially. However, we show quantitatively that there are many fewer MB structures that contain the target variable than there are BN structures that contain it. In particular, the ratio of BN structures to MB structures appears to increase exponentially in the number of variables.

Binary Classifier Calibration: Non-parametric approach

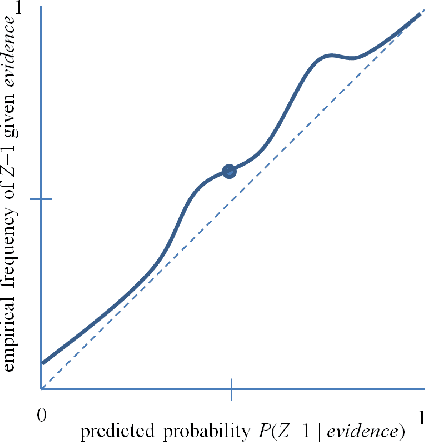
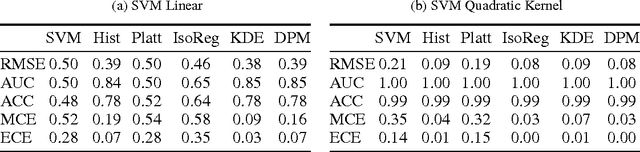
Accurate calibration of probabilistic predictive models learned is critical for many practical prediction and decision-making tasks. There are two main categories of methods for building calibrated classifiers. One approach is to develop methods for learning probabilistic models that are well-calibrated, ab initio. The other approach is to use some post-processing methods for transforming the output of a classifier to be well calibrated, as for example histogram binning, Platt scaling, and isotonic regression. One advantage of the post-processing approach is that it can be applied to any existing probabilistic classification model that was constructed using any machine-learning method. In this paper, we first introduce two measures for evaluating how well a classifier is calibrated. We prove three theorems showing that using a simple histogram binning post-processing method, it is possible to make a classifier be well calibrated while retaining its discrimination capability. Also, by casting the histogram binning method as a density-based non-parametric binary classifier, we can extend it using two simple non-parametric density estimation methods. We demonstrate the performance of the proposed calibration methods on synthetic and real datasets. Experimental results show that the proposed methods either outperform or are comparable to existing calibration methods.

Binary Classifier Calibration: Bayesian Non-Parametric Approach

A set of probabilistic predictions is well calibrated if the events that are predicted to occur with probability p do in fact occur about p fraction of the time. Well calibrated predictions are particularly important when machine learning models are used in decision analysis. This paper presents two new non-parametric methods for calibrating outputs of binary classification models: a method based on the Bayes optimal selection and a method based on the Bayesian model averaging. The advantage of these methods is that they are independent of the algorithm used to learn a predictive model, and they can be applied in a post-processing step, after the model is learned. This makes them applicable to a wide variety of machine learning models and methods. These calibration methods, as well as other methods, are tested on a variety of datasets in terms of both discrimination and calibration performance. The results show the methods either outperform or are comparable in performance to the state-of-the-art calibration methods.

An Algorithm for Computing Probabilistic Propositions

A method for computing probabilistic propositions is presented. It assumes the availability of a single external routine for computing the probability of one instantiated variable, given a conjunction of other instantiated variables. In particular, the method allows belief network algorithms to calculate general probabilistic propositions over nodes in the network. Although in the worst case the time complexity of the method is exponential in the size of a query, it is polynomial in the size of a number of common types of queries.