Obtaining Accurate Probabilistic Causal Inference by Post-Processing Calibration
Paper and Code
Dec 22, 2017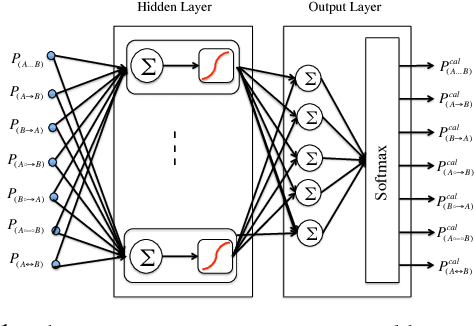
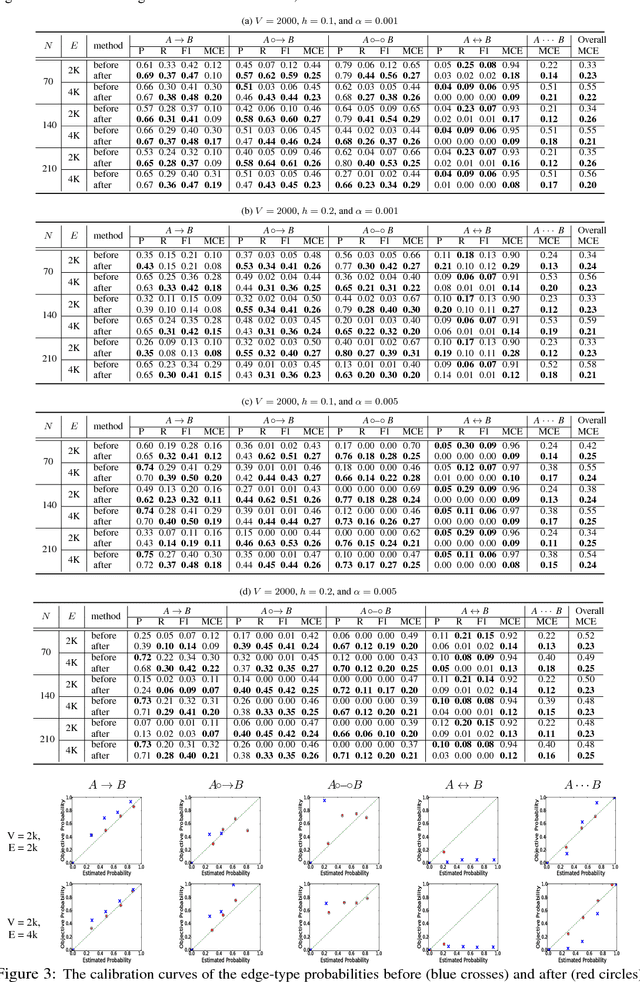
Discovery of an accurate causal Bayesian network structure from observational data can be useful in many areas of science. Often the discoveries are made under uncertainty, which can be expressed as probabilities. To guide the use of such discoveries, including directing further investigation, it is important that those probabilities be well-calibrated. In this paper, we introduce a novel framework to derive calibrated probabilities of causal relationships from observational data. The framework consists of three components: (1) an approximate method for generating initial probability estimates of the edge types for each pair of variables, (2) the availability of a relatively small number of the causal relationships in the network for which the truth status is known, which we call a calibration training set, and (3) a calibration method for using the approximate probability estimates and the calibration training set to generate calibrated probabilities for the many remaining pairs of variables. We also introduce a new calibration method based on a shallow neural network. Our experiments on simulated data support that the proposed approach improves the calibration of causal edge predictions. The results also support that the approach often improves the precision and recall of predictions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge