Causal Markov Boundaries

Feature selection is an important problem in machine learning, which aims to select variables that lead to an optimal predictive model. In this paper, we focus on feature selection for post-intervention outcome prediction from pre-intervention variables. We are motivated by healthcare settings, where the goal is often to select the treatment that will maximize a specific patient's outcome; however, we often do not have sufficient randomized control trial data to identify well the conditional treatment effect. We show how we can use observational data to improve feature selection and effect estimation in two cases: (a) using observational data when we know the causal graph, and (b) when we do not know the causal graph but have observational and limited experimental data. Our paper extends the notion of Markov boundary to treatment-outcome pairs. We provide theoretical guarantees for the methods we introduce. In simulated data, we show that combining observational and experimental data improves feature selection and effect estimation.

Obtaining Accurate Probabilistic Causal Inference by Post-Processing Calibration

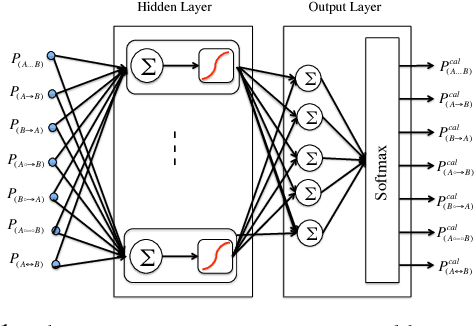
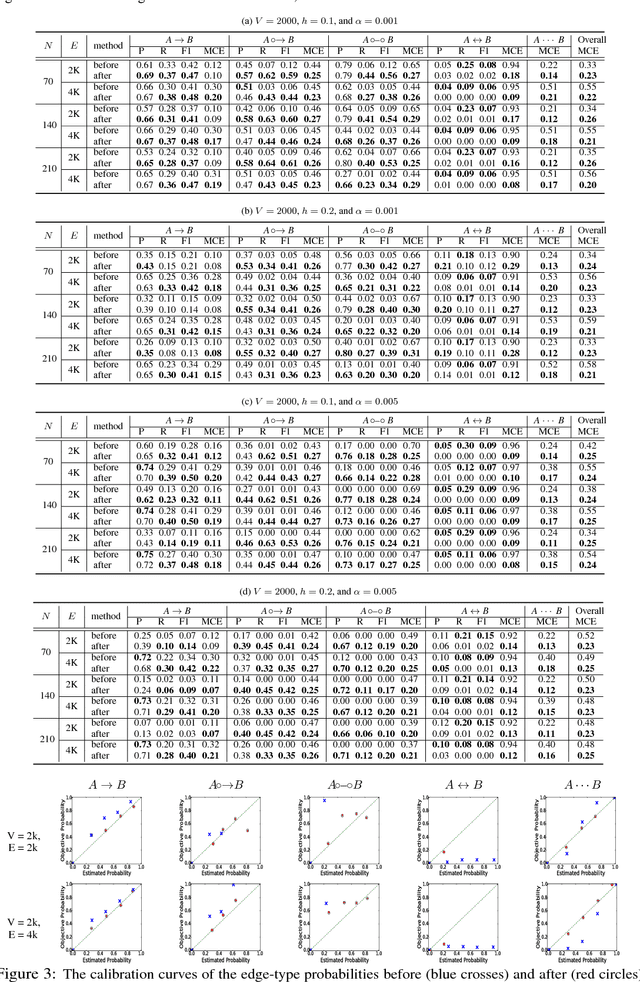
Discovery of an accurate causal Bayesian network structure from observational data can be useful in many areas of science. Often the discoveries are made under uncertainty, which can be expressed as probabilities. To guide the use of such discoveries, including directing further investigation, it is important that those probabilities be well-calibrated. In this paper, we introduce a novel framework to derive calibrated probabilities of causal relationships from observational data. The framework consists of three components: (1) an approximate method for generating initial probability estimates of the edge types for each pair of variables, (2) the availability of a relatively small number of the causal relationships in the network for which the truth status is known, which we call a calibration training set, and (3) a calibration method for using the approximate probability estimates and the calibration training set to generate calibrated probabilities for the many remaining pairs of variables. We also introduce a new calibration method based on a shallow neural network. Our experiments on simulated data support that the proposed approach improves the calibration of causal edge predictions. The results also support that the approach often improves the precision and recall of predictions.