Towards Automated Causal Discovery: a case study on 5G telecommunication data

We introduce the concept of Automated Causal Discovery (AutoCD), defined as any system that aims to fully automate the application of causal discovery and causal reasoning methods. AutoCD's goal is to deliver all causal information that an expert human analyst would and answer a user's causal queries. We describe the architecture of such a platform, and illustrate its performance on synthetic data sets. As a case study, we apply it on temporal telecommunication data. The system is general and can be applied to a plethora of causal discovery problems.

Using Causal Analysis for Conceptual Deep Learning Explanation

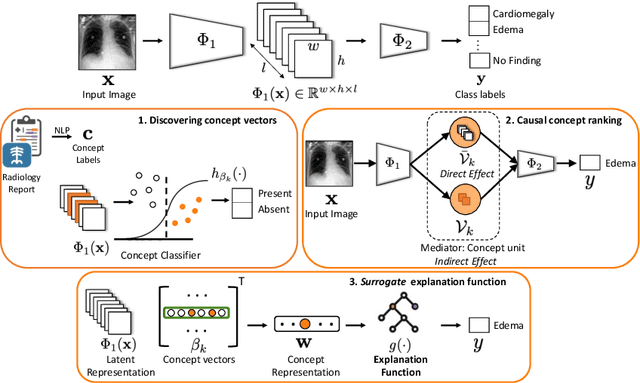
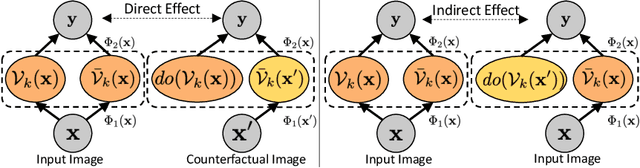
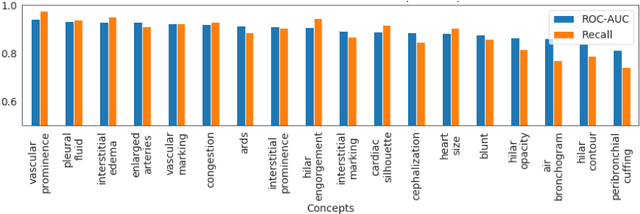
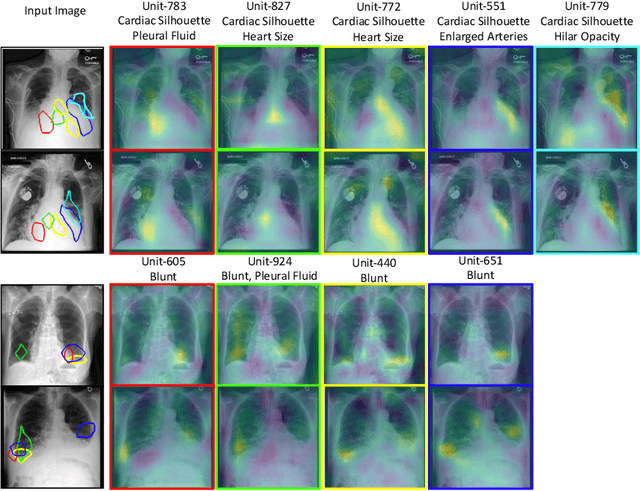
Model explainability is essential for the creation of trustworthy Machine Learning models in healthcare. An ideal explanation resembles the decision-making process of a domain expert and is expressed using concepts or terminology that is meaningful to the clinicians. To provide such an explanation, we first associate the hidden units of the classifier to clinically relevant concepts. We take advantage of radiology reports accompanying the chest X-ray images to define concepts. We discover sparse associations between concepts and hidden units using a linear sparse logistic regression. To ensure that the identified units truly influence the classifier's outcome, we adopt tools from Causal Inference literature and, more specifically, mediation analysis through counterfactual interventions. Finally, we construct a low-depth decision tree to translate all the discovered concepts into a straightforward decision rule, expressed to the radiologist. We evaluated our approach on a large chest x-ray dataset, where our model produces a global explanation consistent with clinical knowledge.

Causal Markov Boundaries

Feature selection is an important problem in machine learning, which aims to select variables that lead to an optimal predictive model. In this paper, we focus on feature selection for post-intervention outcome prediction from pre-intervention variables. We are motivated by healthcare settings, where the goal is often to select the treatment that will maximize a specific patient's outcome; however, we often do not have sufficient randomized control trial data to identify well the conditional treatment effect. We show how we can use observational data to improve feature selection and effect estimation in two cases: (a) using observational data when we know the causal graph, and (b) when we do not know the causal graph but have observational and limited experimental data. Our paper extends the notion of Markov boundary to treatment-outcome pairs. We provide theoretical guarantees for the methods we introduce. In simulated data, we show that combining observational and experimental data improves feature selection and effect estimation.

Learning Adjustment Sets from Observational and Limited Experimental Data

Estimating causal effects from observational data is not always possible due to confounding. Identifying a set of appropriate covariates (adjustment set) and adjusting for their influence can remove confounding bias; however, such a set is typically not identifiable from observational data alone. Experimental data do not have confounding bias, but are typically limited in sample size and can therefore yield imprecise estimates. Furthermore, experimental data often include a limited set of covariates, and therefore provide limited insight into the causal structure of the underlying system. In this work we introduce a method that combines large observational and limited experimental data to identify adjustment sets and improve the estimation of causal effects. The method identifies an adjustment set (if possible) by calculating the marginal likelihood for the experimental data given observationally-derived prior probabilities of potential adjustmen sets. In this way, the method can make inferences that are not possible using only the conditional dependencies and independencies in all the observational and experimental data. We show that the method successfully identifies adjustment sets and improves causal effect estimation in simulated data, and it can sometimes make additional inferences when compared to state-of-the-art methods for combining experimental and observational data.

Rarely-switching linear bandits: optimization of causal effects for the real world

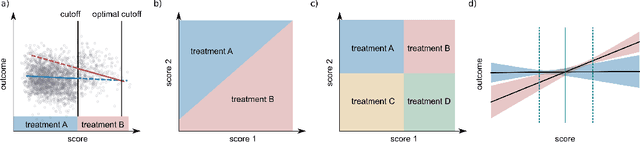
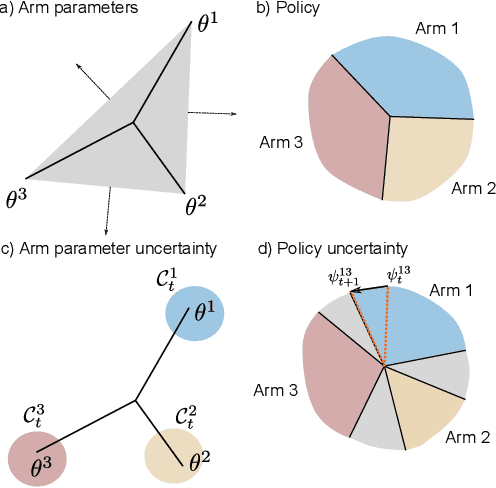
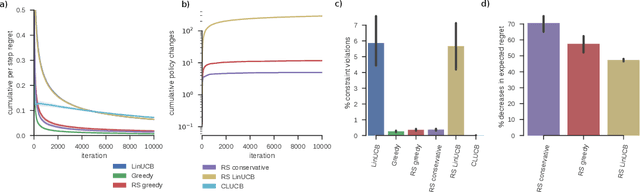
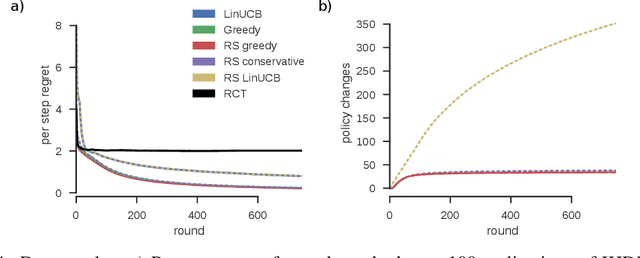
Exploring the effect of policies in many real world scenarios is difficult, unethical, or expensive. After all, doctor guidelines, tax codes, and price lists can only be reprinted so often. We may thus want to only change a policy when it is probable that the change is beneficial. Fortunately, thresholds allow us to estimate treatment effects. Such estimates allows us to optimize the threshold. Here, based on the theory of linear contextual bandits, we present a conservative policy updating procedure which updates a deterministic policy only when needed. We extend the theory of linear bandits to this rarely-switching case, proving such procedures share the same regret, up to constant scaling, as the common LinUCB algorithm. However the algorithm makes far fewer changes to its policy. We provide simulations and an analysis of an infant health well-being causal inference dataset, showing the algorithm efficiently learns a good policy with few changes. Our approach allows efficiently solving problems where changes are to be avoided, with potential applications in economics, medicine and beyond.

Constraint-based Causal Discovery from Multiple Interventions over Overlapping Variable Sets

Scientific practice typically involves repeatedly studying a system, each time trying to unravel a different perspective. In each study, the scientist may take measurements under different experimental conditions (interventions, manipulations, perturbations) and measure different sets of quantities (variables). The result is a collection of heterogeneous data sets coming from different data distributions. In this work, we present algorithm COmbINE, which accepts a collection of data sets over overlapping variable sets under different experimental conditions; COmbINE then outputs a summary of all causal models indicating the invariant and variant structural characteristics of all models that simultaneously fit all of the input data sets. COmbINE converts estimated dependencies and independencies in the data into path constraints on the data-generating causal model and encodes them as a SAT instance. The algorithm is sound and complete in the sample limit. To account for conflicting constraints arising from statistical errors, we introduce a general method for sorting constraints in order of confidence, computed as a function of their corresponding p-values. In our empirical evaluation, COmbINE outperforms in terms of efficiency the only pre-existing similar algorithm; the latter additionally admits feedback cycles, but does not admit conflicting constraints which hinders the applicability on real data. As a proof-of-concept, COmbINE is employed to co-analyze 4 real, mass-cytometry data sets measuring phosphorylated protein concentrations of overlapping protein sets under 3 different interventions.