Assumptions and Bounds in the Instrumental Variable Model

In this note we give proofs for results relating to the Instrumental Variable (IV) model with binary response $Y$ and binary treatment $X$, but with an instrument $Z$ with $K$ states. These results were originally stated in Richardson & Robins (2014), "ACE Bounds; SEMS with Equilibrium Conditions," arXiv:1410.0470.

A Nonparametric Bayes Approach to Online Activity Prediction

Accurately predicting the onset of specific activities within defined timeframes holds significant importance in several applied contexts. In particular, accurate prediction of the number of future users that will be exposed to an intervention is an important piece of information for experimenters running online experiments (A/B tests). In this work, we propose a novel approach to predict the number of users that will be active in a given time period, as well as the temporal trajectory needed to attain a desired user participation threshold. We model user activity using a Bayesian nonparametric approach which allows us to capture the underlying heterogeneity in user engagement. We derive closed-form expressions for the number of new users expected in a given period, and a simple Monte Carlo algorithm targeting the posterior distribution of the number of days needed to attain a desired number of users; the latter is important for experimental planning. We illustrate the performance of our approach via several experiments on synthetic and real world data, in which we show that our novel method outperforms existing competitors.

The m-connecting imset and factorization for ADMG models

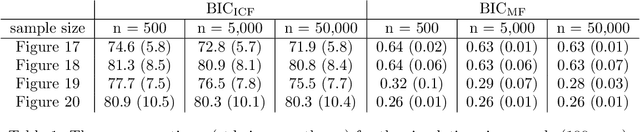
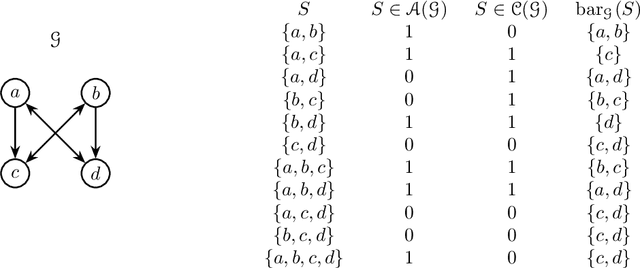
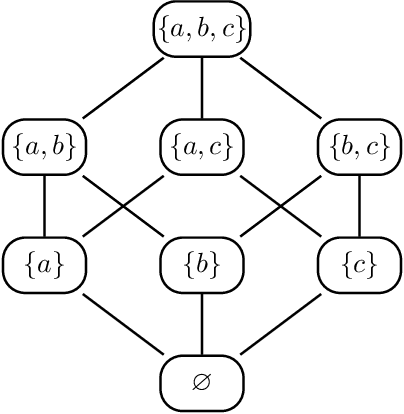
Directed acyclic graph (DAG) models have become widely studied and applied in statistics and machine learning -- indeed, their simplicity facilitates efficient procedures for learning and inference. Unfortunately, these models are not closed under marginalization, making them poorly equipped to handle systems with latent confounding. Acyclic directed mixed graph (ADMG) models characterize margins of DAG models, making them far better suited to handle such systems. However, ADMG models have not seen wide-spread use due to their complexity and a shortage of statistical tools for their analysis. In this paper, we introduce the m-connecting imset which provides an alternative representation for the independence models induced by ADMGs. Furthermore, we define the m-connecting factorization criterion for ADMG models, characterized by a single equation, and prove its equivalence to the global Markov property. The m-connecting imset and factorization criterion provide two new statistical tools for learning and inference with ADMG models. We demonstrate the usefulness of these tools by formulating and evaluating a consistent scoring criterion with a closed form solution.

Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence (2006)

This is the Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence, which was held in Cambridge, MA, July 13 - 16 2006.

A factorization criterion for acyclic directed mixed graphs

Acyclic directed mixed graphs, also known as semi-Markov models represent the conditional independence structure induced on an observed margin by a DAG model with latent variables. In this paper we present a factorization criterion for these models that is equivalent to the global Markov property given by (the natural extension of) d-separation.

Sparse Nested Markov models with Log-linear Parameters

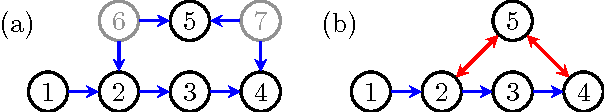
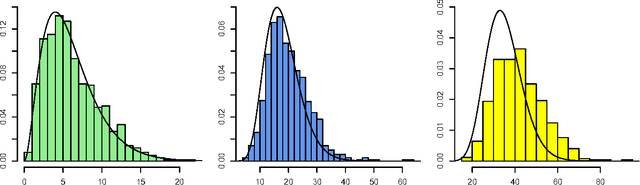
Hidden variables are ubiquitous in practical data analysis, and therefore modeling marginal densities and doing inference with the resulting models is an important problem in statistics, machine learning, and causal inference. Recently, a new type of graphical model, called the nested Markov model, was developed which captures equality constraints found in marginals of directed acyclic graph (DAG) models. Some of these constraints, such as the so called `Verma constraint', strictly generalize conditional independence. To make modeling and inference with nested Markov models practical, it is necessary to limit the number of parameters in the model, while still correctly capturing the constraints in the marginal of a DAG model. Placing such limits is similar in spirit to sparsity methods for undirected graphical models, and regression models. In this paper, we give a log-linear parameterization which allows sparse modeling with nested Markov models. We illustrate the advantages of this parameterization with a simulation study.

Causal Inference in the Presence of Latent Variables and Selection Bias

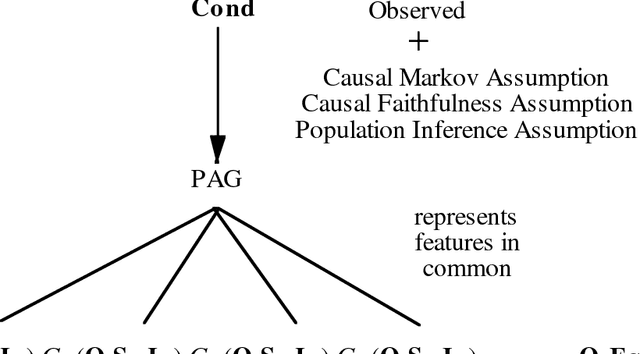
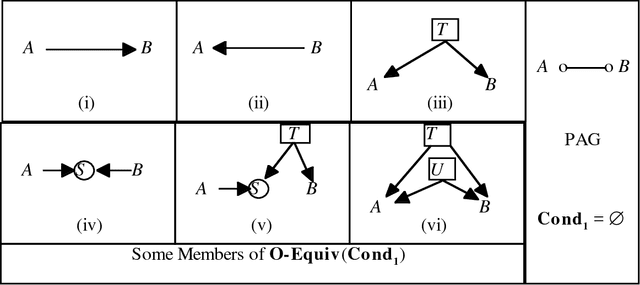
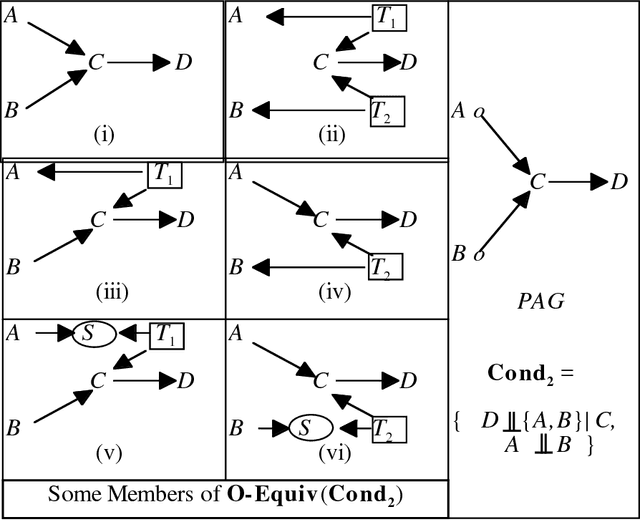
We show that there is a general, informative and reliable procedure for discovering causal relations when, for all the investigator knows, both latent variables and selection bias may be at work. Given information about conditional independence and dependence relations between measured variables, even when latent variables and selection bias may be present, there are sufficient conditions for reliably concluding that there is a causal path from one variable to another, and sufficient conditions for reliably concluding when no such causal path exists.

A Polynomial-Time Algorithm for Deciding Markov Equivalence of Directed Cyclic Graphical Models

Although the concept of d-separation was originally defined for directed acyclic graphs (see Pearl 1988), there is a natural extension of he concept to directed cyclic graphs. When exactly the same set of d-separation relations hold in two directed graphs, no matter whether respectively cyclic or acyclic, we say that they are Markov equivalent. In other words, when two directed cyclic graphs are Markov equivalent, the set of distributions that satisfy a natural extension of the Global Directed Markov condition (Lauritzen et al. 1990) is exactly the same for each graph. There is an obvious exponential (in the number of vertices) time algorithm for deciding Markov equivalence of two directed cyclic graphs; simply chech all of the d-separation relations in each graph. In this paper I state a theorem that gives necessary and sufficient conditions for the Markov equivalence of two directed cyclic graphs, where each of the conditions can be checked in polynomial time. Hence, the theorem can be easily adapted into a polynomial time algorithm for deciding the Markov equivalence of two directed cyclic graphs. Although space prohibits inclusion of correctness proofs, they are fully described in Richardson (1994b).

A Discovery Algorithm for Directed Cyclis Graphs

Directed acyclic graphs have been used fruitfully to represent causal strucures (Pearl 1988). However, in the social sciences and elsewhere models are often used which correspond both causally and statistically to directed graphs with directed cycles (Spirtes 1995). Pearl (1993) discussed predicting the effects of intervention in models of this kind, so-called linear non-recursive structural equation models. This raises the question of whether it is possible to make inferences about causal structure with cycles, form sample data. In particular do there exist general, informative, feasible and reliable precedures for inferring causal structure from conditional independence relations among variables in a sample generated by an unknown causal structure? In this paper I present a discovery algorithm that is correct in the large sample limit, given commonly (but often implicitly) made plausible assumptions, and which provides information about the existence or non-existence of causal pathways from one variable to another. The algorithm is polynomial on sparse graphs.

Cross-covariance modelling via DAGs with hidden variables

DAG models with hidden variables present many difficulties that are not present when all nodes are observed. In particular, fully observed DAG models are identified and correspond to well-defined sets ofdistributions, whereas this is not true if nodes are unobserved. Inthis paper we characterize exactly the set of distributions given by a class of one-dimensional Gaussian latent variable models. These models relate two blocks of observed variables, modeling only the cross-covariance matrix. We describe the relation of this model to the singular value decomposition of the cross-covariance matrix. We show that, although the model is underidentified, useful information may be extracted. We further consider an alternative parametrization in which one latent variable is associated with each block. Our analysis leads to some novel covariance equivalence results for Gaussian hidden variable models.