Student-t processes as infinite-width limits of posterior Bayesian neural networks

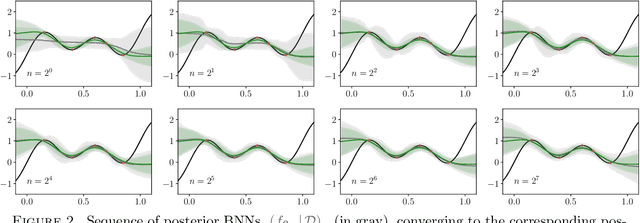
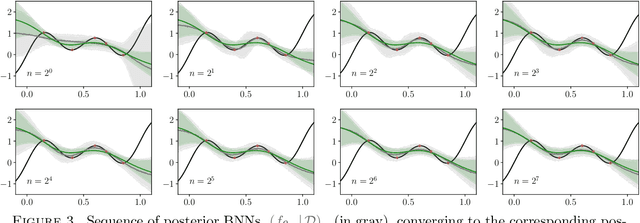
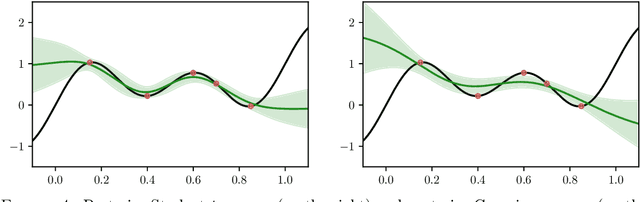
The asymptotic properties of Bayesian Neural Networks (BNNs) have been extensively studied, particularly regarding their approximations by Gaussian processes in the infinite-width limit. We extend these results by showing that posterior BNNs can be approximated by Student-t processes, which offer greater flexibility in modeling uncertainty. Specifically, we show that, if the parameters of a BNN follow a Gaussian prior distribution, and the variance of both the last hidden layer and the Gaussian likelihood function follows an Inverse-Gamma prior distribution, then the resulting posterior BNN converges to a Student-t process in the infinite-width limit. Our proof leverages the Wasserstein metric to establish control over the convergence rate of the Student-t process approximation.

Gaussian credible intervals in Bayesian nonparametric estimation of the unseen

The unseen-species problem assumes $n\geq1$ samples from a population of individuals belonging to different species, possibly infinite, and calls for estimating the number $K_{n,m}$ of hitherto unseen species that would be observed if $m\geq1$ new samples were collected from the same population. This is a long-standing problem in statistics, which has gained renewed relevance in biological and physical sciences, particularly in settings with large values of $n$ and $m$. In this paper, we adopt a Bayesian nonparametric approach to the unseen-species problem under the Pitman-Yor prior, and propose a novel methodology to derive large $m$ asymptotic credible intervals for $K_{n,m}$, for any $n\geq1$. By leveraging a Gaussian central limit theorem for the posterior distribution of $K_{n,m}$, our method improves upon competitors in two key aspects: firstly, it enables the full parameterization of the Pitman-Yor prior, including the Dirichlet prior; secondly, it avoids the need of Monte Carlo sampling, enhancing computational efficiency. We validate the proposed method on synthetic and real data, demonstrating that it improves the empirical performance of competitors by significantly narrowing the gap between asymptotic and exact credible intervals for any $m\geq1$.

Quasi-Bayes empirical Bayes: a sequential approach to the Poisson compound decision problem

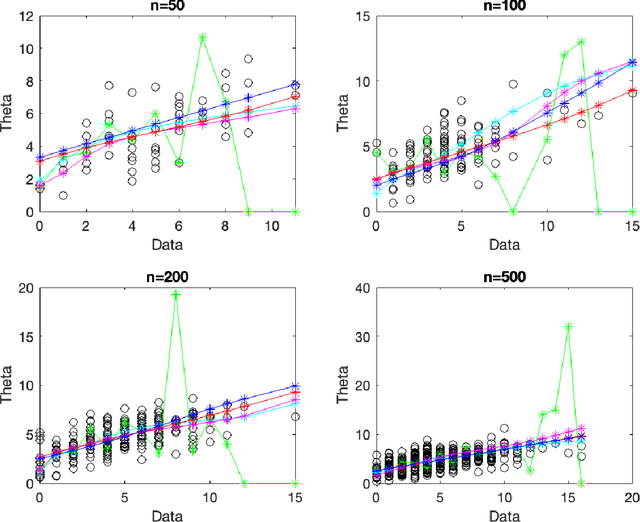
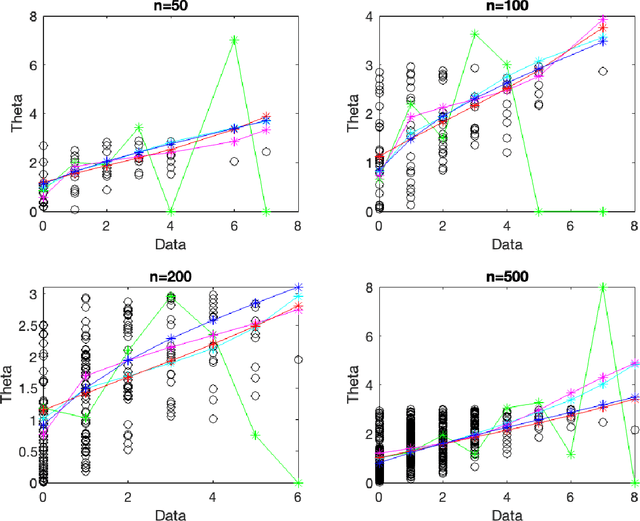
The Poisson compound decision problem is a classical problem in statistics, for which parametric and nonparametric empirical Bayes methodologies are available to estimate the Poisson's means in static or batch domains. In this paper, we consider the Poisson compound decision problem in a streaming or online domain. By relying on a quasi-Bayesian approach, often referred to as Newton's algorithm, we obtain sequential Poisson's mean estimates that are of easy evaluation, computationally efficient and with a constant computational cost as data increase, which is desirable for streaming data. Large sample asymptotic properties of the proposed estimates are investigated, also providing frequentist guarantees in terms of a regret analysis. We validate empirically our methodology, both on synthetic and real data, comparing against the most popular alternatives.

Function-Space MCMC for Bayesian Wide Neural Networks

Bayesian Neural Networks represent a fascinating confluence of deep learning and probabilistic reasoning, offering a compelling framework for understanding uncertainty in complex predictive models. In this paper, we investigate the use of the preconditioned Crank-Nicolson algorithm and its Langevin version to sample from the reparametrised posterior distribution of the weights as the widths of Bayesian Neural Networks grow larger. In addition to being robust in the infinite-dimensional setting, we prove that the acceptance probabilities of the proposed methods approach 1 as the width of the network increases, independently of any stepsize tuning. Moreover, we examine and compare how the mixing speeds of the underdamped Langevin Monte Carlo, the preconditioned Crank-Nicolson and the preconditioned Crank-Nicolson Langevin samplers are influenced by changes in the network width in some real-world cases. Our findings suggest that, in wide Bayesian Neural Networks configurations, the preconditioned Crank-Nicolson method allows for more efficient sampling of the reparametrised posterior distribution, as evidenced by a higher effective sample size and improved diagnostic results compared with the other analysed algorithms.

A quasi-Bayesian sequential approach to deconvolution density estimation

Density deconvolution addresses the estimation of the unknown (probability) density function $f$ of a random signal from data that are observed with an independent additive random noise. This is a classical problem in statistics, for which frequentist and Bayesian nonparametric approaches are available to deal with static or batch data. In this paper, we consider the problem of density deconvolution in a streaming or online setting where noisy data arrive progressively, with no predetermined sample size, and we develop a sequential nonparametric approach to estimate $f$. By relying on a quasi-Bayesian sequential approach, often referred to as Newton's algorithm, we obtain estimates of $f$ that are of easy evaluation, computationally efficient, and with a computational cost that remains constant as the amount of data increases, which is critical in the streaming setting. Large sample asymptotic properties of the proposed estimates are studied, yielding provable guarantees with respect to the estimation of $f$ at a point (local) and on an interval (uniform). In particular, we establish local and uniform central limit theorems, providing corresponding asymptotic credible intervals and bands. We validate empirically our methods on synthetic and real data, by considering the common setting of Laplace and Gaussian noise distributions, and make a comparison with respect to the kernel-based approach and a Bayesian nonparametric approach with a Dirichlet process mixture prior.

Improved prediction of future user activity in online A/B testing

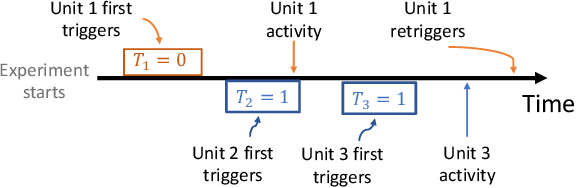
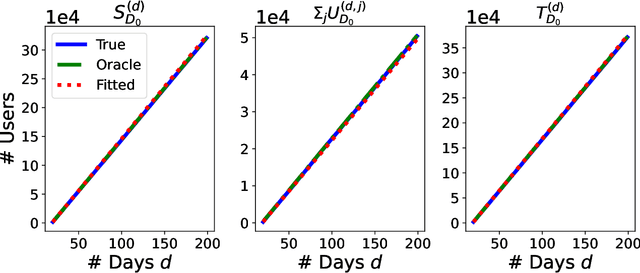
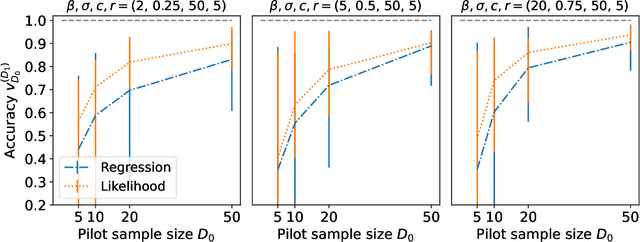
In online randomized experiments or A/B tests, accurate predictions of participant inclusion rates are of paramount importance. These predictions not only guide experimenters in optimizing the experiment's duration but also enhance the precision of treatment effect estimates. In this paper we present a novel, straightforward, and scalable Bayesian nonparametric approach for predicting the rate at which individuals will be exposed to interventions within the realm of online A/B testing. Our approach stands out by offering dual prediction capabilities: it forecasts both the quantity of new customers expected in future time windows and, unlike available alternative methods, the number of times they will be observed. We derive closed-form expressions for the posterior distributions of the quantities needed to form predictions about future user activity, thereby bypassing the need for numerical algorithms such as Markov chain Monte Carlo. After a comprehensive exposition of our model, we test its performance on experiments on real and simulated data, where we show its superior performance with respect to existing alternatives in the literature.

A Nonparametric Bayes Approach to Online Activity Prediction

Accurately predicting the onset of specific activities within defined timeframes holds significant importance in several applied contexts. In particular, accurate prediction of the number of future users that will be exposed to an intervention is an important piece of information for experimenters running online experiments (A/B tests). In this work, we propose a novel approach to predict the number of users that will be active in a given time period, as well as the temporal trajectory needed to attain a desired user participation threshold. We model user activity using a Bayesian nonparametric approach which allows us to capture the underlying heterogeneity in user engagement. We derive closed-form expressions for the number of new users expected in a given period, and a simple Monte Carlo algorithm targeting the posterior distribution of the number of days needed to attain a desired number of users; the latter is important for experimental planning. We illustrate the performance of our approach via several experiments on synthetic and real world data, in which we show that our novel method outperforms existing competitors.

Frequency and cardinality recovery from sketched data: a novel approach bridging Bayesian and frequentist views

We study how to recover the frequency of a symbol in a large discrete data set, using only a compressed representation, or sketch, of those data obtained via random hashing. This is a classical problem in computer science, with various algorithms available, such as the count-min sketch. However, these algorithms often assume that the data are fixed, leading to overly conservative and potentially inaccurate estimates when dealing with randomly sampled data. In this paper, we consider the sketched data as a random sample from an unknown distribution, and then we introduce novel estimators that improve upon existing approaches. Our method combines Bayesian nonparametric and classical (frequentist) perspectives, addressing their unique limitations to provide a principled and practical solution. Additionally, we extend our method to address the related but distinct problem of cardinality recovery, which consists of estimating the total number of distinct objects in the data set. We validate our method on synthetic and real data, comparing its performance to state-of-the-art alternatives.

Quantitative CLTs in Deep Neural Networks

We study the distribution of a fully connected neural network with random Gaussian weights and biases in which the hidden layer widths are proportional to a large constant $n$. Under mild assumptions on the non-linearity, we obtain quantitative bounds on normal approximations valid at large but finite $n$ and any fixed network depth. Our theorems show both for the finite-dimensional distributions and the entire process, that the distance between a random fully connected network (and its derivatives) to the corresponding infinite width Gaussian process scales like $n^{-\gamma}$ for $\gamma>0$, with the exponent depending on the metric used to measure discrepancy. Our bounds are strictly stronger in terms of their dependence on network width than any previously available in the literature; in the one-dimensional case, we also prove that they are optimal, i.e., we establish matching lower bounds.

Non-asymptotic approximations of Gaussian neural networks via second-order Poincaré inequalities

There is a growing interest on large-width asymptotic properties of Gaussian neural networks (NNs), namely NNs whose weights are initialized according to Gaussian distributions. A well-established result is that, as the width goes to infinity, a Gaussian NN converges in distribution to a Gaussian stochastic process, which provides an asymptotic or qualitative Gaussian approximation of the NN. In this paper, we introduce some non-asymptotic or quantitative Gaussian approximations of Gaussian NNs, quantifying the approximation error with respect to some popular distances for (probability) distributions, e.g. the $1$-Wasserstein distance, the total variation distance and the Kolmogorov-Smirnov distance. Our results rely on the use of second-order Gaussian Poincar\'e inequalities, which provide tight estimates of the approximation error, with optimal rates. This is a novel application of second-order Gaussian Poincar\'e inequalities, which are well-known in the probabilistic literature for being a powerful tool to obtain Gaussian approximations of general functionals of Gaussian stochastic processes. A generalization of our results to deep Gaussian NNs is discussed.