Quasi-Bayes empirical Bayes: a sequential approach to the Poisson compound decision problem
Paper and Code
Nov 12, 2024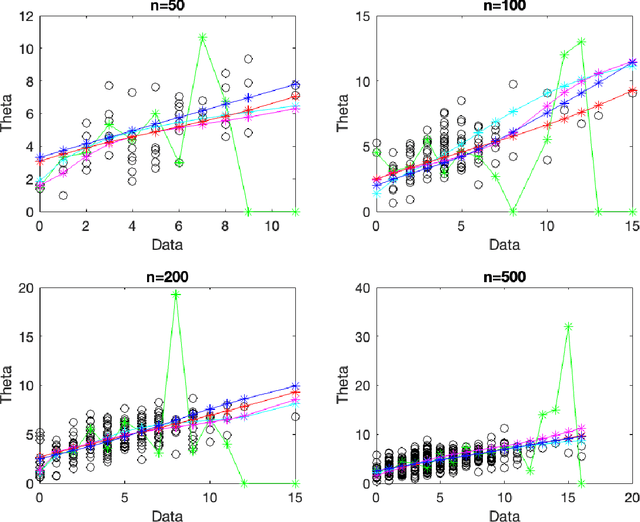


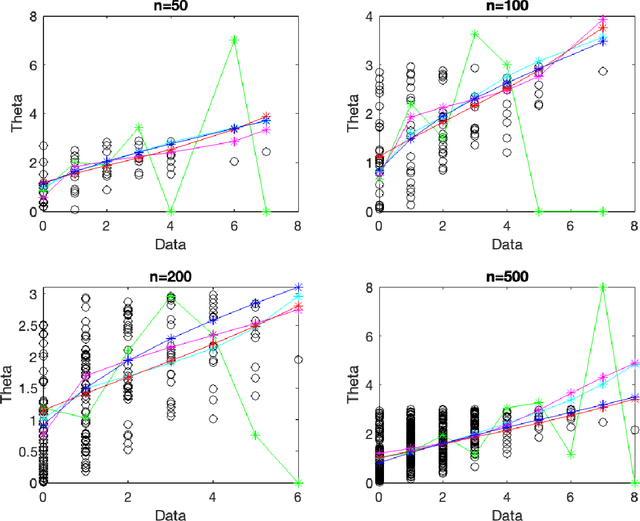
The Poisson compound decision problem is a classical problem in statistics, for which parametric and nonparametric empirical Bayes methodologies are available to estimate the Poisson's means in static or batch domains. In this paper, we consider the Poisson compound decision problem in a streaming or online domain. By relying on a quasi-Bayesian approach, often referred to as Newton's algorithm, we obtain sequential Poisson's mean estimates that are of easy evaluation, computationally efficient and with a constant computational cost as data increase, which is desirable for streaming data. Large sample asymptotic properties of the proposed estimates are investigated, also providing frequentist guarantees in terms of a regret analysis. We validate empirically our methodology, both on synthetic and real data, comparing against the most popular alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge