Quasi-Bayes empirical Bayes: a sequential approach to the Poisson compound decision problem

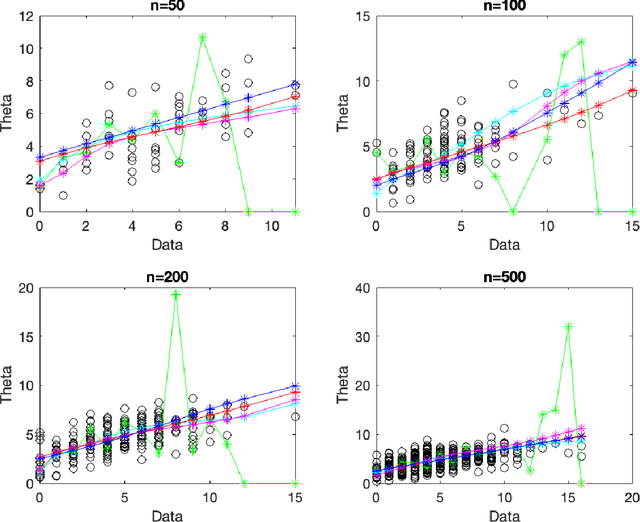
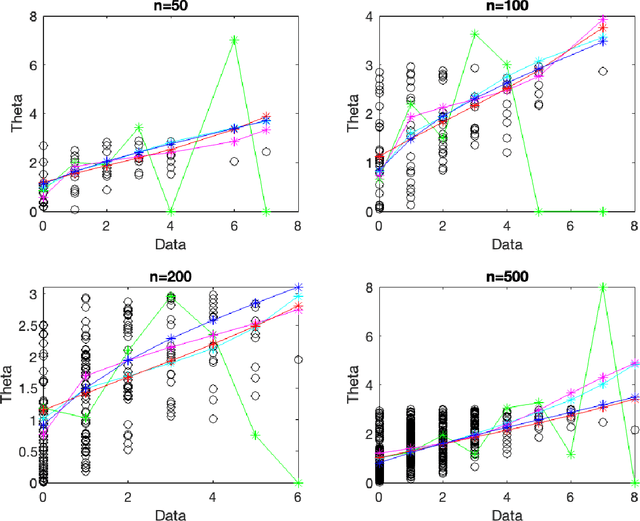
The Poisson compound decision problem is a classical problem in statistics, for which parametric and nonparametric empirical Bayes methodologies are available to estimate the Poisson's means in static or batch domains. In this paper, we consider the Poisson compound decision problem in a streaming or online domain. By relying on a quasi-Bayesian approach, often referred to as Newton's algorithm, we obtain sequential Poisson's mean estimates that are of easy evaluation, computationally efficient and with a constant computational cost as data increase, which is desirable for streaming data. Large sample asymptotic properties of the proposed estimates are investigated, also providing frequentist guarantees in terms of a regret analysis. We validate empirically our methodology, both on synthetic and real data, comparing against the most popular alternatives.

A quasi-Bayesian sequential approach to deconvolution density estimation

Density deconvolution addresses the estimation of the unknown (probability) density function $f$ of a random signal from data that are observed with an independent additive random noise. This is a classical problem in statistics, for which frequentist and Bayesian nonparametric approaches are available to deal with static or batch data. In this paper, we consider the problem of density deconvolution in a streaming or online setting where noisy data arrive progressively, with no predetermined sample size, and we develop a sequential nonparametric approach to estimate $f$. By relying on a quasi-Bayesian sequential approach, often referred to as Newton's algorithm, we obtain estimates of $f$ that are of easy evaluation, computationally efficient, and with a computational cost that remains constant as the amount of data increases, which is critical in the streaming setting. Large sample asymptotic properties of the proposed estimates are studied, yielding provable guarantees with respect to the estimation of $f$ at a point (local) and on an interval (uniform). In particular, we establish local and uniform central limit theorems, providing corresponding asymptotic credible intervals and bands. We validate empirically our methods on synthetic and real data, by considering the common setting of Laplace and Gaussian noise distributions, and make a comparison with respect to the kernel-based approach and a Bayesian nonparametric approach with a Dirichlet process mixture prior.

Non-asymptotic approximations of Gaussian neural networks via second-order Poincaré inequalities

There is a growing interest on large-width asymptotic properties of Gaussian neural networks (NNs), namely NNs whose weights are initialized according to Gaussian distributions. A well-established result is that, as the width goes to infinity, a Gaussian NN converges in distribution to a Gaussian stochastic process, which provides an asymptotic or qualitative Gaussian approximation of the NN. In this paper, we introduce some non-asymptotic or quantitative Gaussian approximations of Gaussian NNs, quantifying the approximation error with respect to some popular distances for (probability) distributions, e.g. the $1$-Wasserstein distance, the total variation distance and the Kolmogorov-Smirnov distance. Our results rely on the use of second-order Gaussian Poincar\'e inequalities, which provide tight estimates of the approximation error, with optimal rates. This is a novel application of second-order Gaussian Poincar\'e inequalities, which are well-known in the probabilistic literature for being a powerful tool to obtain Gaussian approximations of general functionals of Gaussian stochastic processes. A generalization of our results to deep Gaussian NNs is discussed.

Infinitely wide limits for deep Stable neural networks: sub-linear, linear and super-linear activation functions

There is a growing literature on the study of large-width properties of deep Gaussian neural networks (NNs), i.e. deep NNs with Gaussian-distributed parameters or weights, and Gaussian stochastic processes. Motivated by some empirical and theoretical studies showing the potential of replacing Gaussian distributions with Stable distributions, namely distributions with heavy tails, in this paper we investigate large-width properties of deep Stable NNs, i.e. deep NNs with Stable-distributed parameters. For sub-linear activation functions, a recent work has characterized the infinitely wide limit of a suitable rescaled deep Stable NN in terms of a Stable stochastic process, both under the assumption of a ``joint growth" and under the assumption of a ``sequential growth" of the width over the NN's layers. Here, assuming a ``sequential growth" of the width, we extend such a characterization to a general class of activation functions, which includes sub-linear, asymptotically linear and super-linear functions. As a novelty with respect to previous works, our results rely on the use of a generalized central limit theorem for heavy tails distributions, which allows for an interesting unified treatment of infinitely wide limits for deep Stable NNs. Our study shows that the scaling of Stable NNs and the stability of their infinitely wide limits may depend on the choice of the activation function, bringing out a critical difference with respect to the Gaussian setting.

Neural tangent kernel analysis of shallow $α$-Stable ReLU neural networks

There is a recent literature on large-width properties of Gaussian neural networks (NNs), i.e. NNs whose weights are distributed according to Gaussian distributions. Two popular problems are: i) the study of the large-width behaviour of NNs, which provided a characterization of the infinitely wide limit of a rescaled NN in terms of a Gaussian process; ii) the study of the training dynamics of NNs, which set forth a large-width equivalence between training the rescaled NN and performing a kernel regression with a deterministic kernel referred to as the neural tangent kernel (NTK). In this paper, we consider these problems for $\alpha$-Stable NNs, which generalize Gaussian NNs by assuming that the NN's weights are distributed as $\alpha$-Stable distributions with $\alpha\in(0,2]$, i.e. distributions with heavy tails. For shallow $\alpha$-Stable NNs with a ReLU activation function, we show that if the NN's width goes to infinity then a rescaled NN converges weakly to an $\alpha$-Stable process, i.e. a stochastic process with $\alpha$-Stable finite-dimensional distributions. As a novelty with respect to the Gaussian setting, in the $\alpha$-Stable setting the choice of the activation function affects the scaling of the NN, namely: to achieve the infinitely wide $\alpha$-Stable process, the ReLU function requires an additional logarithmic scaling with respect to sub-linear functions. Then, our main contribution is the NTK analysis of shallow $\alpha$-Stable ReLU-NNs, which leads to a large-width equivalence between training a rescaled NN and performing a kernel regression with an $(\alpha/2)$-Stable random kernel. The randomness of such a kernel is a novelty with respect to the Gaussian setting, namely: in the $\alpha$-Stable setting the randomness of the NN at initialization does not vanish in the NTK analysis, thus inducing a distribution for the kernel of the underlying kernel regression.

Deep Stable neural networks: large-width asymptotics and convergence rates

In modern deep learning, there is a recent and growing literature on the interplay between large-width asymptotics for deep Gaussian neural networks (NNs), i.e. deep NNs with Gaussian-distributed weights, and classes of Gaussian stochastic processes (SPs). Such an interplay has proved to be critical in several contexts of practical interest, e.g. Bayesian inference under Gaussian SP priors, kernel regression for infinite-wide deep NNs trained via gradient descent, and information propagation within infinite-wide NNs. Motivated by empirical analysis, showing the potential of replacing Gaussian distributions with Stable distributions for the NN's weights, in this paper we investigate large-width asymptotics for (fully connected) feed-forward deep Stable NNs, i.e. deep NNs with Stable-distributed weights. First, we show that as the width goes to infinity jointly over the NN's layers, a suitable rescaled deep Stable NN converges weakly to a Stable SP whose distribution is characterized recursively through the NN's layers. Because of the non-triangular NN's structure, this is a non-standard asymptotic problem, to which we propose a novel and self-contained inductive approach, which may be of independent interest. Then, we establish sup-norm convergence rates of a deep Stable NN to a Stable SP, quantifying the critical difference between the settings of ``joint growth" and ``sequential growth" of the width over the NN's layers. Our work extends recent results on infinite-wide limits for deep Gaussian NNs to the more general deep Stable NNs, providing the first result on convergence rates for infinite-wide deep NNs.

Large-width functional asymptotics for deep Gaussian neural networks

In this paper, we consider fully connected feed-forward deep neural networks where weights and biases are independent and identically distributed according to Gaussian distributions. Extending previous results (Matthews et al., 2018a;b; Yang, 2019) we adopt a function-space perspective, i.e. we look at neural networks as infinite-dimensional random elements on the input space $\mathbb{R}^I$. Under suitable assumptions on the activation function we show that: i) a network defines a continuous Gaussian process on the input space $\mathbb{R}^I$; ii) a network with re-scaled weights converges weakly to a continuous Gaussian process in the large-width limit; iii) the limiting Gaussian process has almost surely locally $\gamma$-H\"older continuous paths, for $0 < \gamma <1$. Our results contribute to recent theoretical studies on the interplay between infinitely wide deep neural networks and Gaussian processes by establishing weak convergence in function-space with respect to a stronger metric.

Infinite-channel deep stable convolutional neural networks

The interplay between infinite-width neural networks (NNs) and classes of Gaussian processes (GPs) is well known since the seminal work of Neal (1996). While numerous theoretical refinements have been proposed in the recent years, the interplay between NNs and GPs relies on two critical distributional assumptions on the NN's parameters: A1) finite variance; A2) independent and identical distribution (iid). In this paper, we consider the problem of removing A1 in the general context of deep feed-forward convolutional NNs. In particular, we assume iid parameters distributed according to a stable distribution and we show that the infinite-channel limit of a deep feed-forward convolutional NNs, under suitable scaling, is a stochastic process with multivariate stable finite-dimensional distributions. Such a limiting distribution is then characterized through an explicit backward recursion for its parameters over the layers. Our contribution extends results of Favaro et al. (2020) to convolutional architectures, and it paves the way to expand exciting recent lines of research that rely on classes of GP limits.

Stable behaviour of infinitely wide deep neural networks

We consider fully connected feed-forward deep neural networks (NNs) where weights and biases are independent and identically distributed as symmetric centered stable distributions. Then, we show that the infinite wide limit of the NN, under suitable scaling on the weights, is a stochastic process whose finite-dimensional distributions are multivariate stable distributions. The limiting process is referred to as the stable process, and it generalizes the class of Gaussian processes recently obtained as infinite wide limits of NNs (Matthews at al., 2018b). Parameters of the stable process can be computed via an explicit recursion over the layers of the network. Our result contributes to the theory of fully connected feed-forward deep NNs, and it paves the way to expand recent lines of research that rely on Gaussian infinite wide limits.