Optimal Nonlinear Online Learning under Sequential Price Competition via s-Concavity

We consider price competition among multiple sellers over a selling horizon of $T$ periods. In each period, sellers simultaneously offer their prices and subsequently observe their respective demand that is unobservable to competitors. The demand function for each seller depends on all sellers' prices through a private, unknown, and nonlinear relationship. To address this challenge, we propose a semi-parametric least-squares estimation of the nonlinear mean function, which does not require sellers to communicate demand information. We show that when all sellers employ our policy, their prices converge at a rate of $O(T^{-1/7})$ to the Nash equilibrium prices that sellers would reach if they were fully informed. Each seller incurs a regret of $O(T^{5/7})$ relative to a dynamic benchmark policy. A theoretical contribution of our work is proving the existence of equilibrium under shape-constrained demand functions via the concept of $s$-concavity and establishing regret bounds of our proposed policy. Technically, we also establish new concentration results for the least squares estimator under shape constraints. Our findings offer significant insights into dynamic competition-aware pricing and contribute to the broader study of non-parametric learning in strategic decision-making.

Dynamic Pricing in the Linear Valuation Model using Shape Constraints

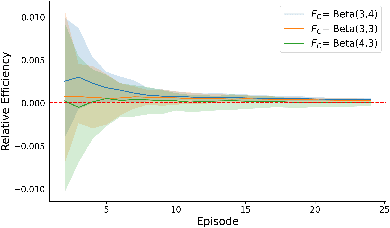
We propose a shape-constrained approach to dynamic pricing for censored data in the linear valuation model that eliminates the need for tuning parameters commonly required in existing methods. Previous works have addressed the challenge of unknown market noise distribution F using strategies ranging from kernel methods to reinforcement learning algorithms, such as bandit techniques and upper confidence bounds (UCB), under the Lipschitz (and stronger) assumption(s) on $F_0$. In contrast, our method relies on isotonic regression under the weaker assumption that $F_0$ is $\alpha$-Holder continuous for some $\alpha \in (0,1]$. We obtain an upper bound on the asymptotic expected regret that matches existing bounds in the literature for $\alpha = 1$ (the Lipschitz case). Simulations and experiments with real-world data obtained by Welltower Inc (a major healthcare Real Estate Investment Trust) consistently demonstrate that our method attains better empirical regret in comparison to several existing methods in the literature while offering the advantage of being completely tuning-parameter free.

Microfoundation Inference for Strategic Prediction

Often in prediction tasks, the predictive model itself can influence the distribution of the target variable, a phenomenon termed performative prediction. Generally, this influence stems from strategic actions taken by stakeholders with a vested interest in predictive models. A key challenge that hinders the widespread adaptation of performative prediction in machine learning is that practitioners are generally unaware of the social impacts of their predictions. To address this gap, we propose a methodology for learning the distribution map that encapsulates the long-term impacts of predictive models on the population. Specifically, we model agents' responses as a cost-adjusted utility maximization problem and propose estimates for said cost. Our approach leverages optimal transport to align pre-model exposure (ex ante) and post-model exposure (ex post) distributions. We provide a rate of convergence for this proposed estimate and assess its quality through empirical demonstrations on a credit-scoring dataset.

Learning the Distribution Map in Reverse Causal Performative Prediction

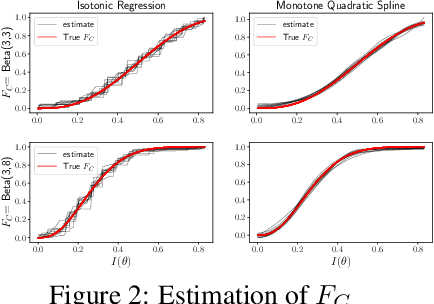
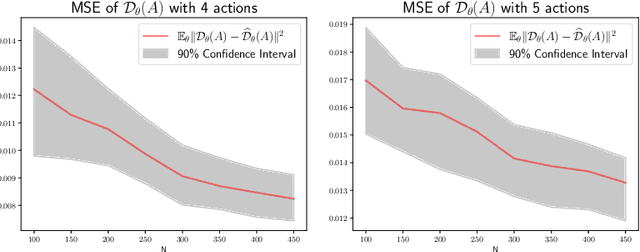
In numerous predictive scenarios, the predictive model affects the sampling distribution; for example, job applicants often meticulously craft their resumes to navigate through a screening systems. Such shifts in distribution are particularly prevalent in the realm of social computing, yet, the strategies to learn these shifts from data remain remarkably limited. Inspired by a microeconomic model that adeptly characterizes agents' behavior within labor markets, we introduce a novel approach to learn the distribution shift. Our method is predicated on a reverse causal model, wherein the predictive model instigates a distribution shift exclusively through a finite set of agents' actions. Within this framework, we employ a microfoundation model for the agents' actions and develop a statistically justified methodology to learn the distribution shift map, which we demonstrate to be effective in minimizing the performative prediction risk.

Large-width functional asymptotics for deep Gaussian neural networks

In this paper, we consider fully connected feed-forward deep neural networks where weights and biases are independent and identically distributed according to Gaussian distributions. Extending previous results (Matthews et al., 2018a;b; Yang, 2019) we adopt a function-space perspective, i.e. we look at neural networks as infinite-dimensional random elements on the input space $\mathbb{R}^I$. Under suitable assumptions on the activation function we show that: i) a network defines a continuous Gaussian process on the input space $\mathbb{R}^I$; ii) a network with re-scaled weights converges weakly to a continuous Gaussian process in the large-width limit; iii) the limiting Gaussian process has almost surely locally $\gamma$-H\"older continuous paths, for $0 < \gamma <1$. Our results contribute to recent theoretical studies on the interplay between infinitely wide deep neural networks and Gaussian processes by establishing weak convergence in function-space with respect to a stronger metric.

Infinite-channel deep stable convolutional neural networks

The interplay between infinite-width neural networks (NNs) and classes of Gaussian processes (GPs) is well known since the seminal work of Neal (1996). While numerous theoretical refinements have been proposed in the recent years, the interplay between NNs and GPs relies on two critical distributional assumptions on the NN's parameters: A1) finite variance; A2) independent and identical distribution (iid). In this paper, we consider the problem of removing A1 in the general context of deep feed-forward convolutional NNs. In particular, we assume iid parameters distributed according to a stable distribution and we show that the infinite-channel limit of a deep feed-forward convolutional NNs, under suitable scaling, is a stochastic process with multivariate stable finite-dimensional distributions. Such a limiting distribution is then characterized through an explicit backward recursion for its parameters over the layers. Our contribution extends results of Favaro et al. (2020) to convolutional architectures, and it paves the way to expand exciting recent lines of research that rely on classes of GP limits.