Kevin Stoll
Dynamic Pricing in the Linear Valuation Model using Shape Constraints
Feb 09, 2025


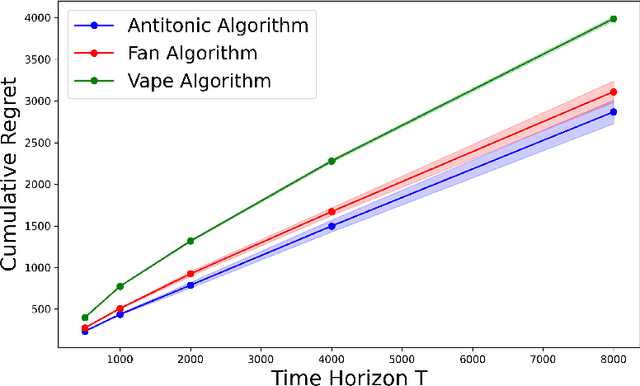
Abstract:We propose a shape-constrained approach to dynamic pricing for censored data in the linear valuation model that eliminates the need for tuning parameters commonly required in existing methods. Previous works have addressed the challenge of unknown market noise distribution F using strategies ranging from kernel methods to reinforcement learning algorithms, such as bandit techniques and upper confidence bounds (UCB), under the Lipschitz (and stronger) assumption(s) on $F_0$. In contrast, our method relies on isotonic regression under the weaker assumption that $F_0$ is $\alpha$-Holder continuous for some $\alpha \in (0,1]$. We obtain an upper bound on the asymptotic expected regret that matches existing bounds in the literature for $\alpha = 1$ (the Lipschitz case). Simulations and experiments with real-world data obtained by Welltower Inc (a major healthcare Real Estate Investment Trust) consistently demonstrate that our method attains better empirical regret in comparison to several existing methods in the literature while offering the advantage of being completely tuning-parameter free.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge