Optimal Nonlinear Online Learning under Sequential Price Competition via s-Concavity

We consider price competition among multiple sellers over a selling horizon of $T$ periods. In each period, sellers simultaneously offer their prices and subsequently observe their respective demand that is unobservable to competitors. The demand function for each seller depends on all sellers' prices through a private, unknown, and nonlinear relationship. To address this challenge, we propose a semi-parametric least-squares estimation of the nonlinear mean function, which does not require sellers to communicate demand information. We show that when all sellers employ our policy, their prices converge at a rate of $O(T^{-1/7})$ to the Nash equilibrium prices that sellers would reach if they were fully informed. Each seller incurs a regret of $O(T^{5/7})$ relative to a dynamic benchmark policy. A theoretical contribution of our work is proving the existence of equilibrium under shape-constrained demand functions via the concept of $s$-concavity and establishing regret bounds of our proposed policy. Technically, we also establish new concentration results for the least squares estimator under shape constraints. Our findings offer significant insights into dynamic competition-aware pricing and contribute to the broader study of non-parametric learning in strategic decision-making.

Likelihood-Free Estimation for Spatiotemporal Hawkes processes with missing data and application to predictive policing

With the growing use of AI technology, many police departments use forecasting software to predict probable crime hotspots and allocate patrolling resources effectively for crime prevention. The clustered nature of crime data makes self-exciting Hawkes processes a popular modeling choice. However, one significant challenge in fitting such models is the inherent missingness in crime data due to non-reporting, which can bias the estimated parameters of the predictive model, leading to inaccurate downstream hotspot forecasts, often resulting in over or under-policing in various communities, especially the vulnerable ones. Our work introduces a Wasserstein Generative Adversarial Networks (WGAN) driven likelihood-free approach to account for unreported crimes in Spatiotemporal Hawkes models. We demonstrate through empirical analysis how this methodology improves the accuracy of parametric estimation in the presence of data missingness, leading to more reliable and efficient policing strategies.

Dynamic Pricing in the Linear Valuation Model using Shape Constraints

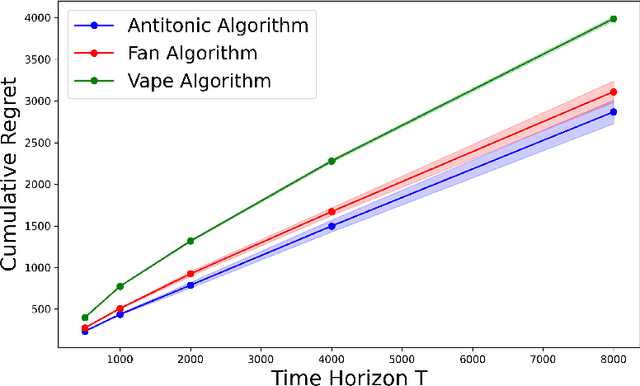
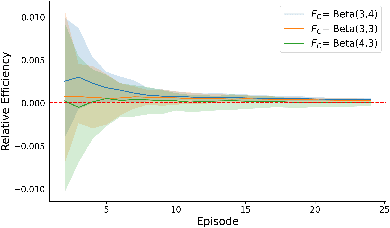
We propose a shape-constrained approach to dynamic pricing for censored data in the linear valuation model that eliminates the need for tuning parameters commonly required in existing methods. Previous works have addressed the challenge of unknown market noise distribution F using strategies ranging from kernel methods to reinforcement learning algorithms, such as bandit techniques and upper confidence bounds (UCB), under the Lipschitz (and stronger) assumption(s) on $F_0$. In contrast, our method relies on isotonic regression under the weaker assumption that $F_0$ is $\alpha$-Holder continuous for some $\alpha \in (0,1]$. We obtain an upper bound on the asymptotic expected regret that matches existing bounds in the literature for $\alpha = 1$ (the Lipschitz case). Simulations and experiments with real-world data obtained by Welltower Inc (a major healthcare Real Estate Investment Trust) consistently demonstrate that our method attains better empirical regret in comparison to several existing methods in the literature while offering the advantage of being completely tuning-parameter free.

Microfoundation Inference for Strategic Prediction

Often in prediction tasks, the predictive model itself can influence the distribution of the target variable, a phenomenon termed performative prediction. Generally, this influence stems from strategic actions taken by stakeholders with a vested interest in predictive models. A key challenge that hinders the widespread adaptation of performative prediction in machine learning is that practitioners are generally unaware of the social impacts of their predictions. To address this gap, we propose a methodology for learning the distribution map that encapsulates the long-term impacts of predictive models on the population. Specifically, we model agents' responses as a cost-adjusted utility maximization problem and propose estimates for said cost. Our approach leverages optimal transport to align pre-model exposure (ex ante) and post-model exposure (ex post) distributions. We provide a rate of convergence for this proposed estimate and assess its quality through empirical demonstrations on a credit-scoring dataset.

A statistical framework for weak-to-strong generalization

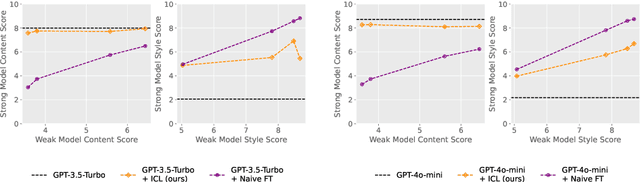
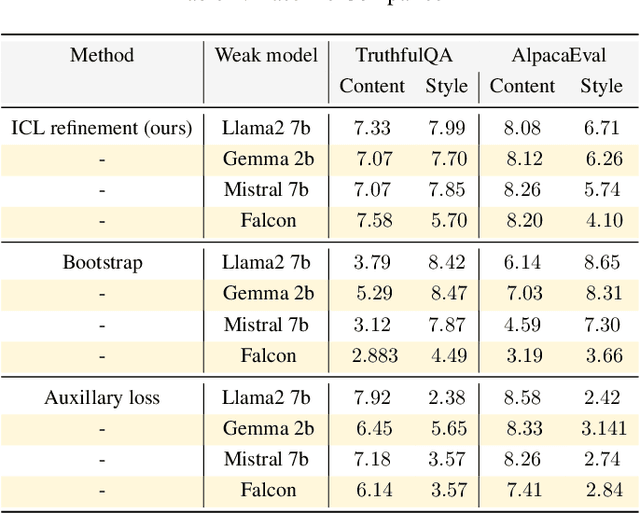
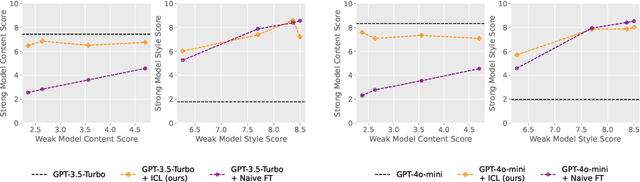
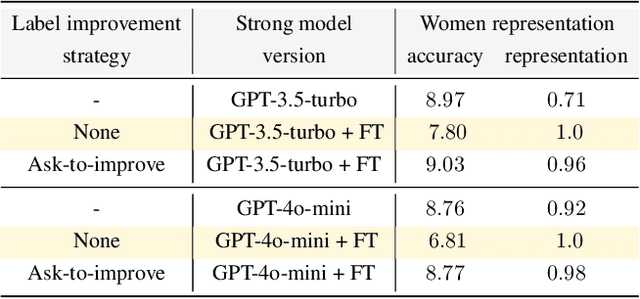
Modern large language model (LLM) alignment techniques rely on human feedback, but it is unclear whether the techniques fundamentally limit the capabilities of aligned LLMs. In particular, it is unclear whether it is possible to align (stronger) LLMs with superhuman capabilities with (weaker) human feedback without degrading their capabilities. This is an instance of the weak-to-strong generalization problem: using weaker (less capable) feedback to train a stronger (more capable) model. We prove that weak-to-strong generalization is possible by eliciting latent knowledge from pre-trained LLMs. In particular, we cast the weak-to-strong generalization problem as a transfer learning problem in which we wish to transfer a latent concept from a weak model to a strong pre-trained model. We prove that a naive fine-tuning approach suffers from fundamental limitations, but an alternative refinement-based approach suggested by the problem structure provably overcomes the limitations of fine-tuning. Finally, we demonstrate the practical applicability of the refinement approach with three LLM alignment tasks.

Learning the Distribution Map in Reverse Causal Performative Prediction

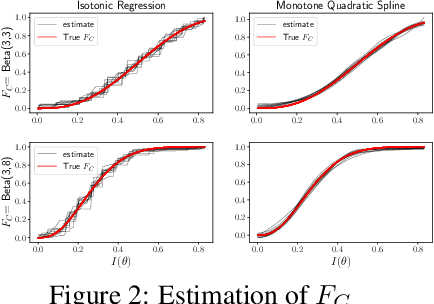
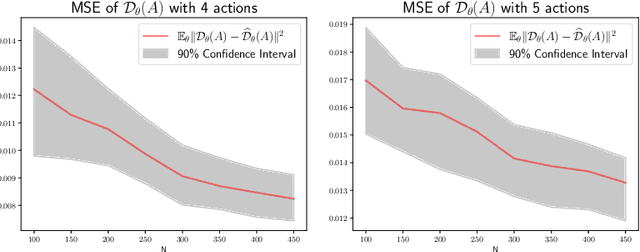
In numerous predictive scenarios, the predictive model affects the sampling distribution; for example, job applicants often meticulously craft their resumes to navigate through a screening systems. Such shifts in distribution are particularly prevalent in the realm of social computing, yet, the strategies to learn these shifts from data remain remarkably limited. Inspired by a microeconomic model that adeptly characterizes agents' behavior within labor markets, we introduce a novel approach to learn the distribution shift. Our method is predicated on a reverse causal model, wherein the predictive model instigates a distribution shift exclusively through a finite set of agents' actions. Within this framework, we employ a microfoundation model for the agents' actions and develop a statistically justified methodology to learn the distribution shift map, which we demonstrate to be effective in minimizing the performative prediction risk.

Estimating Fréchet bounds for validating programmatic weak supervision

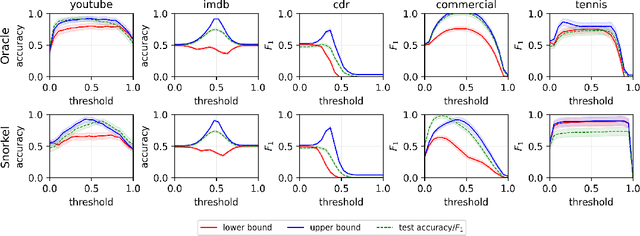
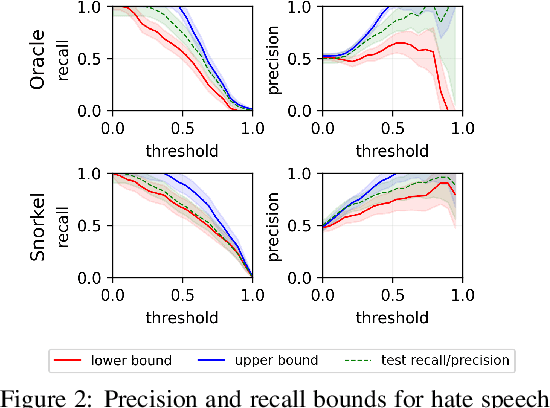
We develop methods for estimating Fr\'echet bounds on (possibly high-dimensional) distribution classes in which some variables are continuous-valued. We establish the statistical correctness of the computed bounds under uncertainty in the marginal constraints and demonstrate the usefulness of our algorithms by evaluating the performance of machine learning (ML) models trained with programmatic weak supervision (PWS). PWS is a framework for principled learning from weak supervision inputs (e.g., crowdsourced labels, knowledge bases, pre-trained models on related tasks, etc), and it has achieved remarkable success in many areas of science and engineering. Unfortunately, it is generally difficult to validate the performance of ML models trained with PWS due to the absence of labeled data. Our algorithms address this issue by estimating sharp lower and upper bounds for performance metrics such as accuracy/recall/precision/F1 score.

Conditional independence testing under model misspecification

Conditional independence (CI) testing is fundamental and challenging in modern statistics and machine learning. Many modern methods for CI testing rely on powerful supervised learning methods to learn regression functions or Bayes predictors as an intermediate step. Although the methods are guaranteed to control Type-I error when the supervised learning methods accurately estimate the regression functions or Bayes predictors, their behavior is less understood when they fail due to model misspecification. In a broader sense, model misspecification can arise even when universal approximators (e.g., deep neural nets) are employed. Then, we study the performance of regression-based CI tests under model misspecification. Namely, we propose new approximations or upper bounds for the testing errors of three regression-based tests that depend on misspecification errors. Moreover, we introduce the Rao-Blackwellized Predictor Test (RBPT), a novel regression-based CI test robust against model misspecification. Finally, we conduct experiments with artificial and real data, showcasing the usefulness of our theory and methods.

Understanding new tasks through the lens of training data via exponential tilting

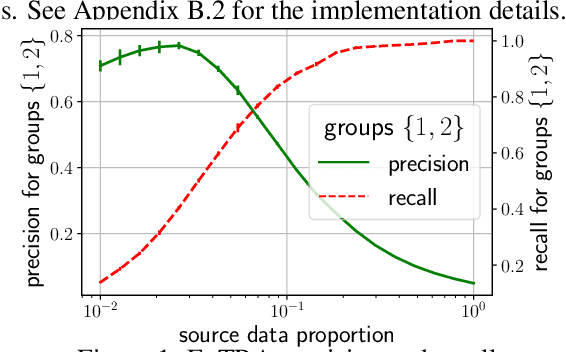
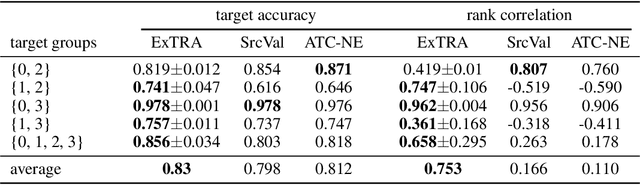
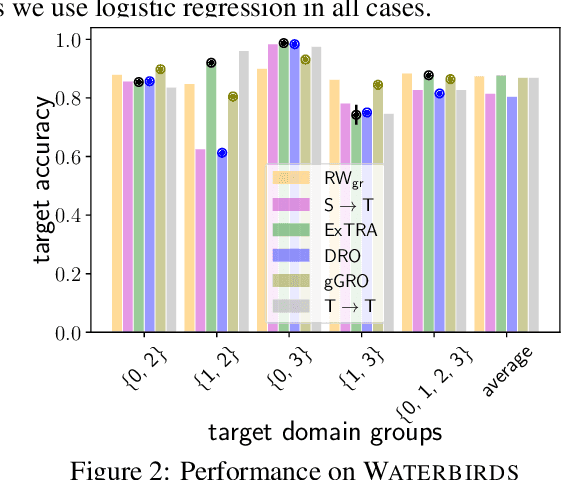
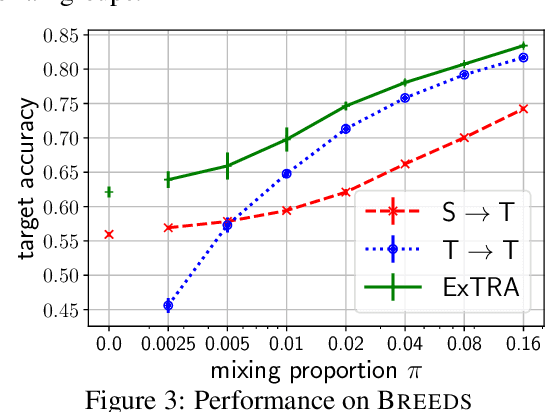
Deploying machine learning models to new tasks is a major challenge despite the large size of the modern training datasets. However, it is conceivable that the training data can be reweighted to be more representative of the new (target) task. We consider the problem of reweighing the training samples to gain insights into the distribution of the target task. Specifically, we formulate a distribution shift model based on the exponential tilt assumption and learn train data importance weights minimizing the KL divergence between labeled train and unlabeled target datasets. The learned train data weights can then be used for downstream tasks such as target performance evaluation, fine-tuning, and model selection. We demonstrate the efficacy of our method on Waterbirds and Breeds benchmarks.

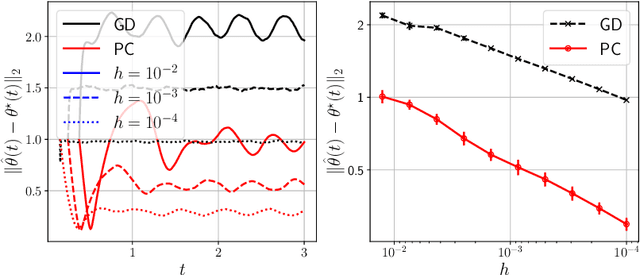
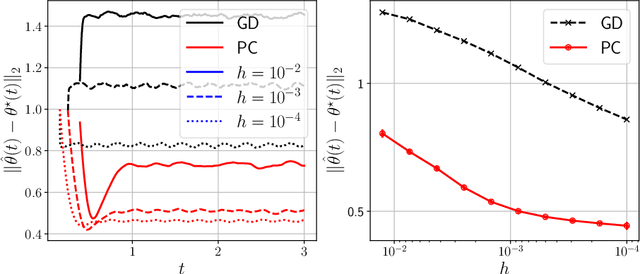
Predictor-corrector algorithms for stochastic optimization under gradual distribution shift

Time-varying stochastic optimization problems frequently arise in machine learning practice (e.g. gradual domain shift, object tracking, strategic classification). Although most problems are solved in discrete time, the underlying process is often continuous in nature. We exploit this underlying continuity by developing predictor-corrector algorithms for time-varying stochastic optimizations. We provide error bounds for the iterates, both in presence of pure and noisy access to the queries from the relevant derivatives of the loss function. Furthermore, we show (theoretically and empirically in several examples) that our method outperforms non-predictor corrector methods that do not exploit the underlying continuous process.