Estimating Fréchet bounds for validating programmatic weak supervision
Paper and Code
Dec 07, 2023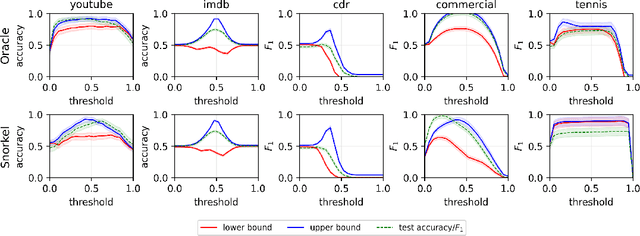

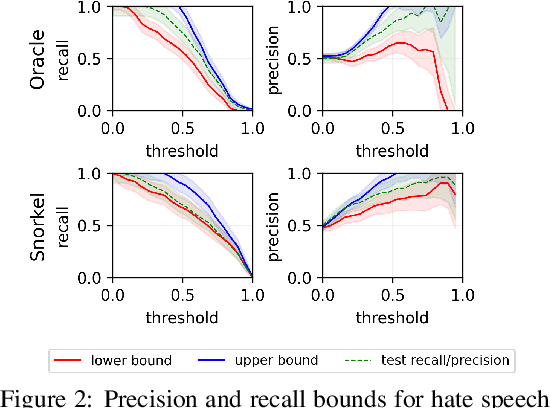

We develop methods for estimating Fr\'echet bounds on (possibly high-dimensional) distribution classes in which some variables are continuous-valued. We establish the statistical correctness of the computed bounds under uncertainty in the marginal constraints and demonstrate the usefulness of our algorithms by evaluating the performance of machine learning (ML) models trained with programmatic weak supervision (PWS). PWS is a framework for principled learning from weak supervision inputs (e.g., crowdsourced labels, knowledge bases, pre-trained models on related tasks, etc), and it has achieved remarkable success in many areas of science and engineering. Unfortunately, it is generally difficult to validate the performance of ML models trained with PWS due to the absence of labeled data. Our algorithms address this issue by estimating sharp lower and upper bounds for performance metrics such as accuracy/recall/precision/F1 score.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge