Predictor-corrector algorithms for stochastic optimization under gradual distribution shift
Paper and Code
May 26, 2022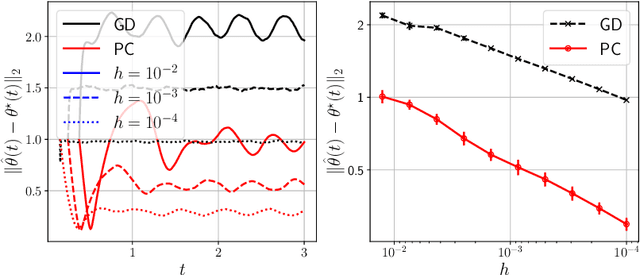
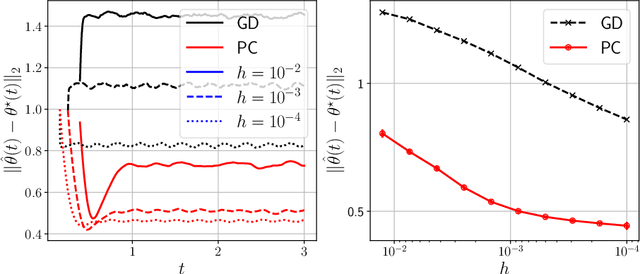
Time-varying stochastic optimization problems frequently arise in machine learning practice (e.g. gradual domain shift, object tracking, strategic classification). Although most problems are solved in discrete time, the underlying process is often continuous in nature. We exploit this underlying continuity by developing predictor-corrector algorithms for time-varying stochastic optimizations. We provide error bounds for the iterates, both in presence of pure and noisy access to the queries from the relevant derivatives of the loss function. Furthermore, we show (theoretically and empirically in several examples) that our method outperforms non-predictor corrector methods that do not exploit the underlying continuous process.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge