On the estimation rate of Bayesian PINN for inverse problems

Solving partial differential equations (PDEs) and their inverse problems using Physics-informed neural networks (PINNs) is a rapidly growing approach in the physics and machine learning community. Although several architectures exist for PINNs that work remarkably in practice, our theoretical understanding of their performances is somewhat limited. In this work, we study the behavior of a Bayesian PINN estimator of the solution of a PDE from $n$ independent noisy measurement of the solution. We focus on a class of equations that are linear in their parameters (with unknown coefficients $\theta_\star$). We show that when the partial differential equation admits a classical solution (say $u_\star$), differentiable to order $\beta$, the mean square error of the Bayesian posterior mean is at least of order $n^{-2\beta/(2\beta + d)}$. Furthermore, we establish a convergence rate of the linear coefficients of $\theta_\star$ depending on the order of the underlying differential operator. Last but not least, our theoretical results are validated through extensive simulations.

Optimal Aggregation of Prediction Intervals under Unsupervised Domain Shift

As machine learning models are increasingly deployed in dynamic environments, it becomes paramount to assess and quantify uncertainties associated with distribution shifts. A distribution shift occurs when the underlying data-generating process changes, leading to a deviation in the model's performance. The prediction interval, which captures the range of likely outcomes for a given prediction, serves as a crucial tool for characterizing uncertainties induced by their underlying distribution. In this paper, we propose methodologies for aggregating prediction intervals to obtain one with minimal width and adequate coverage on the target domain under unsupervised domain shift, under which we have labeled samples from a related source domain and unlabeled covariates from the target domain. Our analysis encompasses scenarios where the source and the target domain are related via i) a bounded density ratio, and ii) a measure-preserving transformation. Our proposed methodologies are computationally efficient and easy to implement. Beyond illustrating the performance of our method through a real-world dataset, we also delve into the theoretical details. This includes establishing rigorous theoretical guarantees, coupled with finite sample bounds, regarding the coverage and width of our prediction intervals. Our approach excels in practical applications and is underpinned by a solid theoretical framework, ensuring its reliability and effectiveness across diverse contexts.

Trade-off Between Dependence and Complexity for Nonparametric Learning -- an Empirical Process Approach

Empirical process theory for i.i.d. observations has emerged as a ubiquitous tool for understanding the generalization properties of various statistical problems. However, in many applications where the data exhibit temporal dependencies (e.g., in finance, medical imaging, weather forecasting etc.), the corresponding empirical processes are much less understood. Motivated by this observation, we present a general bound on the expected supremum of empirical processes under standard $\beta/\rho$-mixing assumptions. Unlike most prior work, our results cover both the long and the short-range regimes of dependence. Our main result shows that a non-trivial trade-off between the complexity of the underlying function class and the dependence among the observations characterizes the learning rate in a large class of nonparametric problems. This trade-off reveals a new phenomenon, namely that even under long-range dependence, it is possible to attain the same rates as in the i.i.d. setting, provided the underlying function class is complex enough. We demonstrate the practical implications of our findings by analyzing various statistical estimators in both fixed and growing dimensions. Our main examples include a comprehensive case study of generalization error bounds in nonparametric regression over smoothness classes in fixed as well as growing dimension using neural nets, shape-restricted multivariate convex regression, estimating the optimal transport (Wasserstein) distance between two probability distributions, and classification under the Mammen-Tsybakov margin condition -- all under appropriate mixing assumptions. In the process, we also develop bounds on $L_r$ ($1\le r\le 2$)-localized empirical processes with dependent observations, which we then leverage to get faster rates for (a) tuning-free adaptation, and (b) set-structured learning problems.

UTOPIA: Universally Trainable Optimal Prediction Intervals Aggregation

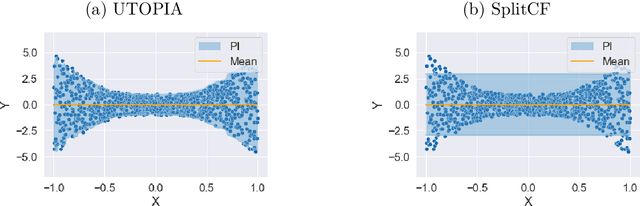
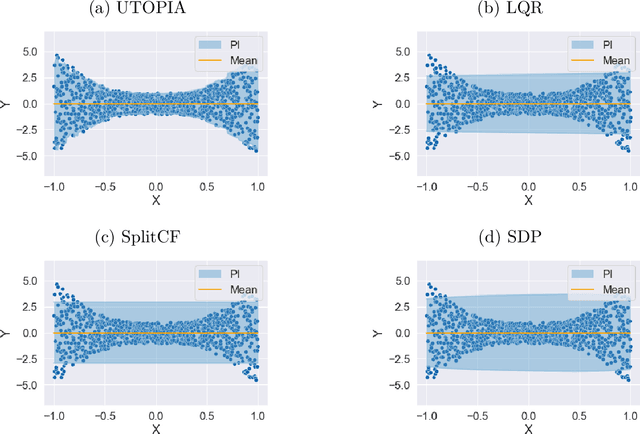
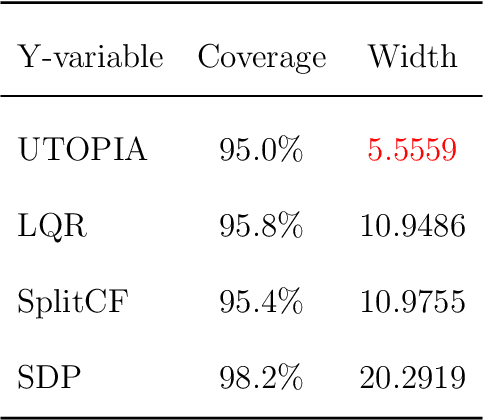
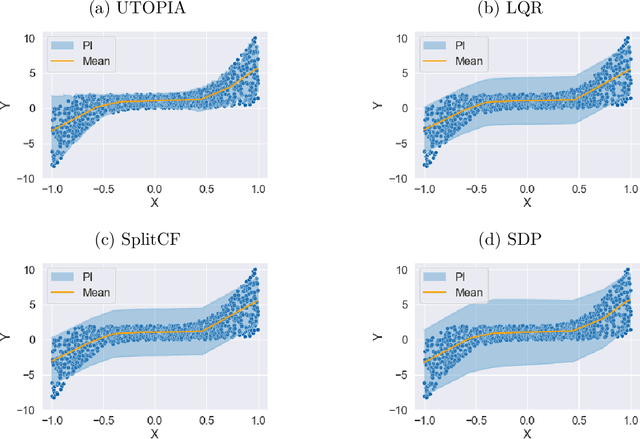
Uncertainty quantification for prediction is an intriguing problem with significant applications in various fields, such as biomedical science, economic studies, and weather forecasts. Numerous methods are available for constructing prediction intervals, such as quantile regression and conformal predictions, among others. Nevertheless, model misspecification (especially in high-dimension) or sub-optimal constructions can frequently result in biased or unnecessarily-wide prediction intervals. In this paper, we propose a novel and widely applicable technique for aggregating multiple prediction intervals to minimize the average width of the prediction band along with coverage guarantee, called Universally Trainable Optimal Predictive Intervals Aggregation (UTOPIA). The method also allows us to directly construct predictive bands based on elementary basis functions. Our approach is based on linear or convex programming which is easy to implement. All of our proposed methodologies are supported by theoretical guarantees on the coverage probability and optimal average length, which are detailed in this paper. The effectiveness of our approach is convincingly demonstrated by applying it to synthetic data and two real datasets on finance and macroeconomics.

Deep Neural Networks for Nonparametric Interaction Models with Diverging Dimension

Deep neural networks have achieved tremendous success due to their representation power and adaptation to low-dimensional structures. Their potential for estimating structured regression functions has been recently established in the literature. However, most of the studies require the input dimension to be fixed and consequently ignore the effect of dimension on the rate of convergence and hamper their applications to modern big data with high dimensionality. In this paper, we bridge this gap by analyzing a $k^{th}$ order nonparametric interaction model in both growing dimension scenarios ($d$ grows with $n$ but at a slower rate) and in high dimension ($d \gtrsim n$). In the latter case, sparsity assumptions and associated regularization are required in order to obtain optimal rates of convergence. A new challenge in diverging dimension setting is in calculation mean-square error, the covariance terms among estimated additive components are an order of magnitude larger than those of the variances and they can deteriorate statistical properties without proper care. We introduce a critical debiasing technique to amend the problem. We show that under certain standard assumptions, debiased deep neural networks achieve a minimax optimal rate both in terms of $(n, d)$. Our proof techniques rely crucially on a novel debiasing technique that makes the covariances of additive components negligible in the mean-square error calculation. In addition, we establish the matching lower bounds.

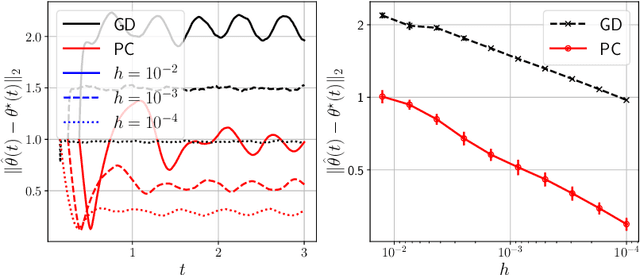
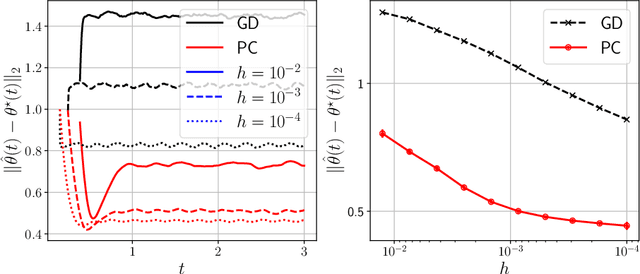
Predictor-corrector algorithms for stochastic optimization under gradual distribution shift

Time-varying stochastic optimization problems frequently arise in machine learning practice (e.g. gradual domain shift, object tracking, strategic classification). Although most problems are solved in discrete time, the underlying process is often continuous in nature. We exploit this underlying continuity by developing predictor-corrector algorithms for time-varying stochastic optimizations. We provide error bounds for the iterates, both in presence of pure and noisy access to the queries from the relevant derivatives of the loss function. Furthermore, we show (theoretically and empirically in several examples) that our method outperforms non-predictor corrector methods that do not exploit the underlying continuous process.

Domain Adaptation meets Individual Fairness. And they get along

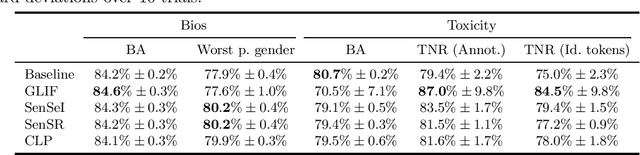
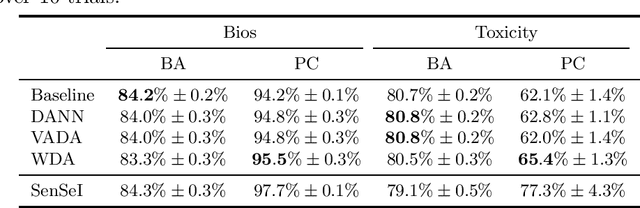
Many instances of algorithmic bias are caused by distributional shifts. For example, machine learning (ML) models often perform worse on demographic groups that are underrepresented in the training data. In this paper, we leverage this connection between algorithmic fairness and distribution shifts to show that algorithmic fairness interventions can help ML models overcome distribution shifts, and that domain adaptation methods (for overcoming distribution shifts) can mitigate algorithmic biases. In particular, we show that (i) enforcing suitable notions of individual fairness (IF) can improve the out-of-distribution accuracy of ML models, and that (ii) it is possible to adapt representation alignment methods for domain adaptation to enforce (individual) fairness. The former is unexpected because IF interventions were not developed with distribution shifts in mind. The latter is also unexpected because representation alignment is not a common approach in the IF literature.

Post-processing for Individual Fairness

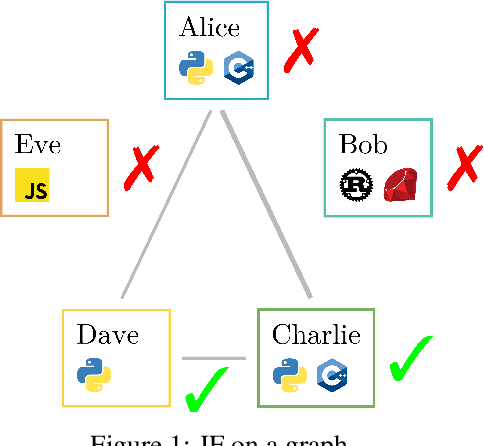
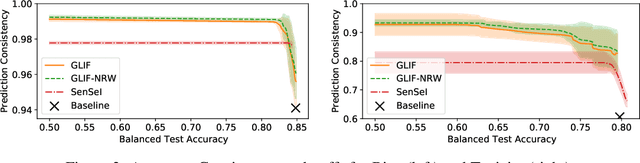
Post-processing in algorithmic fairness is a versatile approach for correcting bias in ML systems that are already used in production. The main appeal of post-processing is that it avoids expensive retraining. In this work, we propose general post-processing algorithms for individual fairness (IF). We consider a setting where the learner only has access to the predictions of the original model and a similarity graph between individuals, guiding the desired fairness constraints. We cast the IF post-processing problem as a graph smoothing problem corresponding to graph Laplacian regularization that preserves the desired "treat similar individuals similarly" interpretation. Our theoretical results demonstrate the connection of the new objective function to a local relaxation of the original individual fairness. Empirically, our post-processing algorithms correct individual biases in large-scale NLP models such as BERT, while preserving accuracy.

There is no trade-off: enforcing fairness can improve accuracy

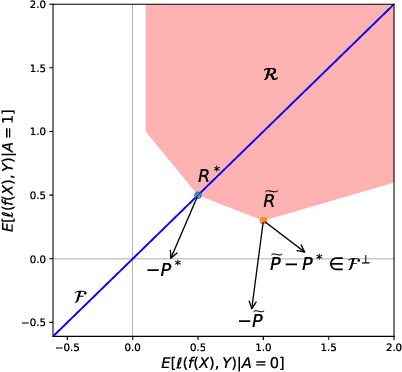
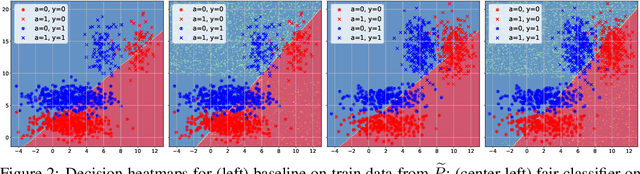
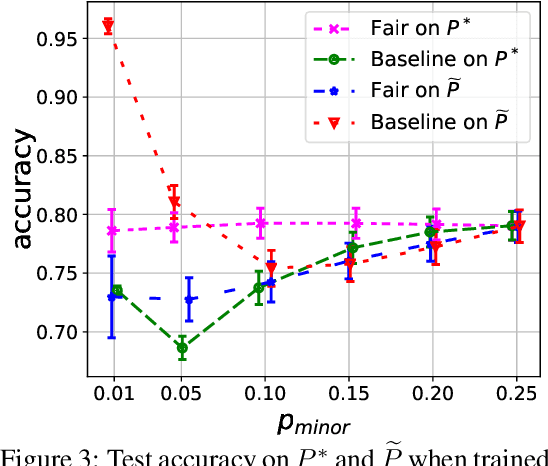
One of the main barriers to the broader adoption of algorithmic fairness in machine learning is the trade-off between fairness and performance of ML models: many practitioners are unwilling to sacrifice the performance of their ML model for fairness. In this paper, we show that this trade-off may not be necessary. If the algorithmic biases in an ML model are due to sampling biases in the training data, then enforcing algorithmic fairness may improve the performance of the ML model on unbiased test data. We study conditions under which enforcing algorithmic fairness helps practitioners learn the Bayes decision rule for (unbiased) test data from biased training data. We also demonstrate the practical implications of our theoretical results in real-world ML tasks.

Two Simple Ways to Learn Individual Fairness Metrics from Data

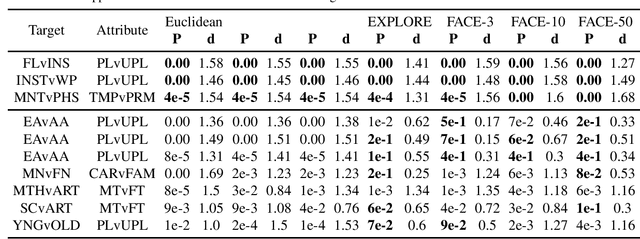
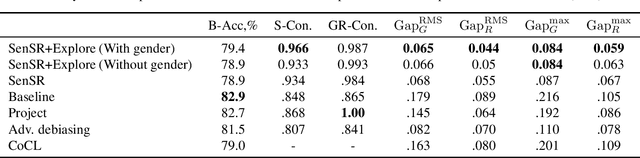
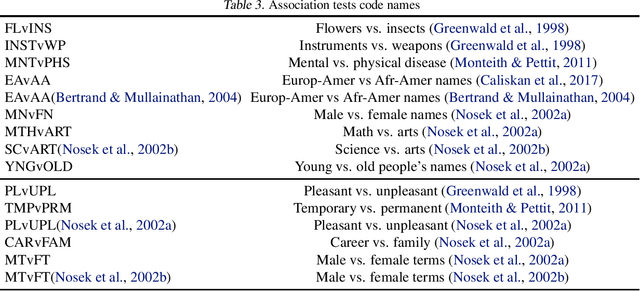
Individual fairness is an intuitive definition of algorithmic fairness that addresses some of the drawbacks of group fairness. Despite its benefits, it depends on a task specific fair metric that encodes our intuition of what is fair and unfair for the ML task at hand, and the lack of a widely accepted fair metric for many ML tasks is the main barrier to broader adoption of individual fairness. In this paper, we present two simple ways to learn fair metrics from a variety of data types. We show empirically that fair training with the learned metrics leads to improved fairness on three machine learning tasks susceptible to gender and racial biases. We also provide theoretical guarantees on the statistical performance of both approaches.