Data-driven rainfall prediction at a regional scale: a case study with Ghana

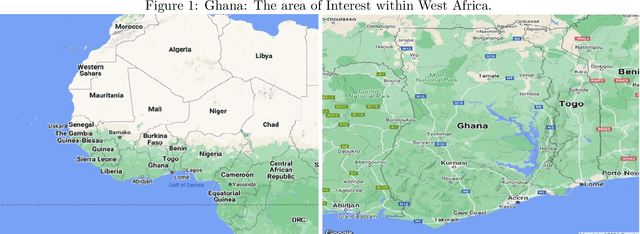
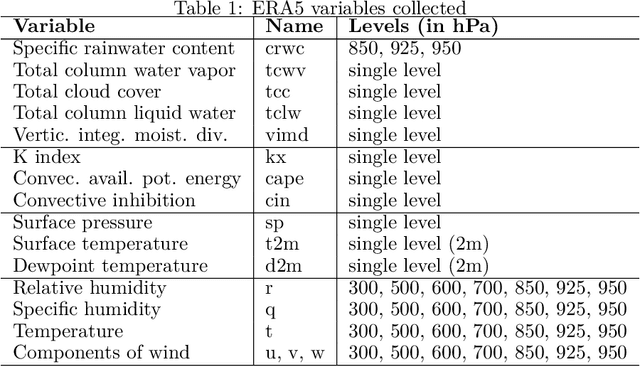
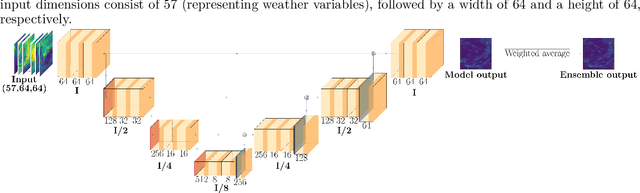
With a warming planet, tropical regions are expected to experience the brunt of climate change, with more intense and more volatile rainfall events. Currently, state-of-the-art numerical weather prediction (NWP) models are known to struggle to produce skillful rainfall forecasts in tropical regions of Africa. There is thus a pressing need for improved rainfall forecasting in these regions. Over the last decade or so, the increased availability of large-scale meteorological datasets and the development of powerful machine learning models have opened up new opportunities for data-driven weather forecasting. Focusing on Ghana in this study, we use these tools to develop two U-Net convolutional neural network (CNN) models, to predict 24h rainfall at 12h and 30h lead-time. The models were trained using data from the ERA5 reanalysis dataset, and the GPM-IMERG dataset. A special attention was paid to interpretability. We developed a novel statistical methodology that allowed us to probe the relative importance of the meteorological variables input in our model, offering useful insights into the factors that drive precipitation in the Ghana region. Empirically, we found that our 12h lead-time model has performances that match, and in some accounts are better than the 18h lead-time forecasts produced by the ECMWF (as available in the TIGGE dataset). We also found that combining our data-driven model with classical NWP further improves forecast accuracy.

On the estimation rate of Bayesian PINN for inverse problems

Solving partial differential equations (PDEs) and their inverse problems using Physics-informed neural networks (PINNs) is a rapidly growing approach in the physics and machine learning community. Although several architectures exist for PINNs that work remarkably in practice, our theoretical understanding of their performances is somewhat limited. In this work, we study the behavior of a Bayesian PINN estimator of the solution of a PDE from $n$ independent noisy measurement of the solution. We focus on a class of equations that are linear in their parameters (with unknown coefficients $\theta_\star$). We show that when the partial differential equation admits a classical solution (say $u_\star$), differentiable to order $\beta$, the mean square error of the Bayesian posterior mean is at least of order $n^{-2\beta/(2\beta + d)}$. Furthermore, we establish a convergence rate of the linear coefficients of $\theta_\star$ depending on the order of the underlying differential operator. Last but not least, our theoretical results are validated through extensive simulations.

On Cyclical MCMC Sampling

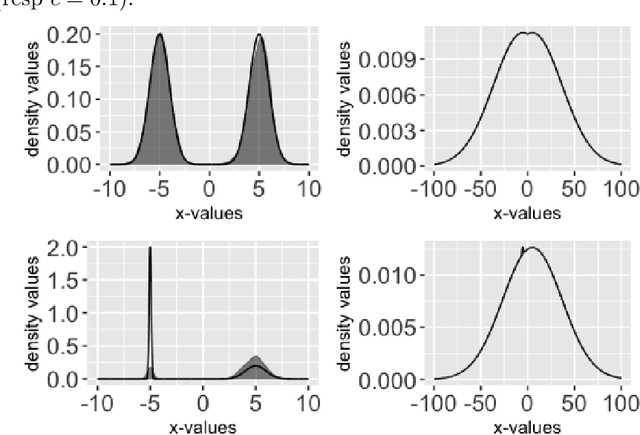
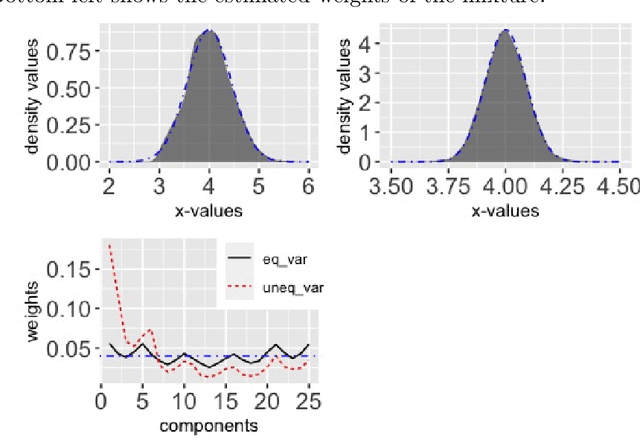
Cyclical MCMC is a novel MCMC framework recently proposed by Zhang et al. (2019) to address the challenge posed by high-dimensional multimodal posterior distributions like those arising in deep learning. The algorithm works by generating a nonhomogeneous Markov chain that tracks -- cyclically in time -- tempered versions of the target distribution. We show in this work that cyclical MCMC converges to the desired probability distribution in settings where the Markov kernels used are fast mixing, and sufficiently long cycles are employed. However in the far more common settings of slow mixing kernels, the algorithm may fail to produce samples from the desired distribution. In particular, in a simple mixture example with unequal variance, we show by simulation that cyclical MCMC fails to converge to the desired limit. Finally, we show that cyclical MCMC typically estimates well the local shape of the target distribution around each mode, even when we do not have convergence to the target.

A statistical perspective on algorithm unrolling models for inverse problems

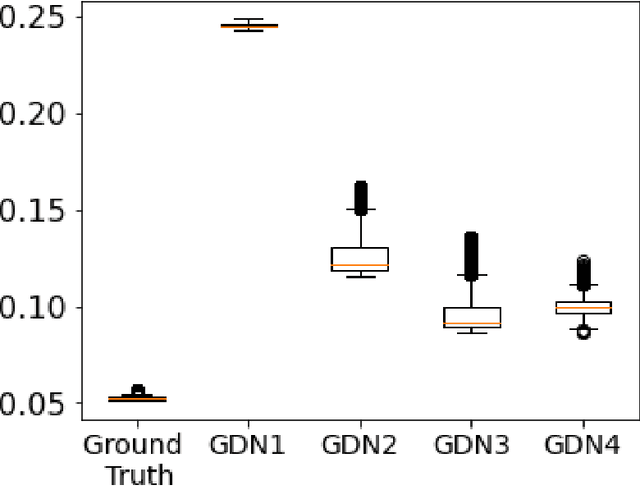
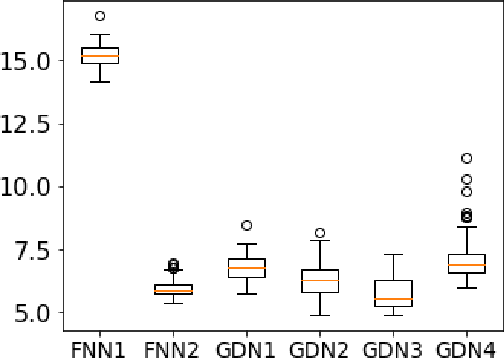
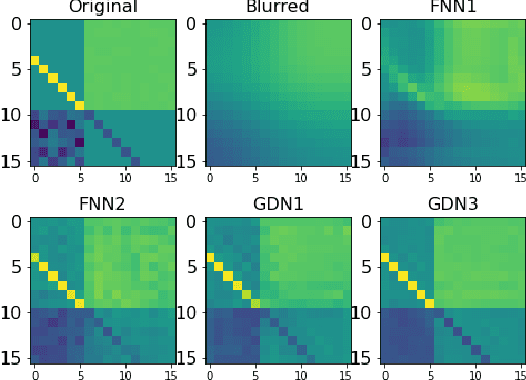
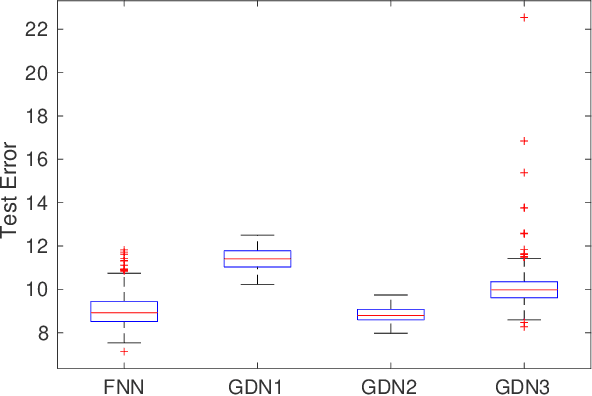
We consider inverse problems where the conditional distribution of the observation ${\bf y}$ given the latent variable of interest ${\bf x}$ (also known as the forward model) is known, and we have access to a data set in which multiple instances of ${\bf x}$ and ${\bf y}$ are both observed. In this context, algorithm unrolling has become a very popular approach for designing state-of-the-art deep neural network architectures that effectively exploit the forward model. We analyze the statistical complexity of the gradient descent network (GDN), an algorithm unrolling architecture driven by proximal gradient descent. We show that the unrolling depth needed for the optimal statistical performance of GDNs is of order $\log(n)/\log(\varrho_n^{-1})$, where $n$ is the sample size, and $\varrho_n$ is the convergence rate of the corresponding gradient descent algorithm. We also show that when the negative log-density of the latent variable ${\bf x}$ has a simple proximal operator, then a GDN unrolled at depth $D'$ can solve the inverse problem at the parametric rate $O(D'/\sqrt{n})$. Our results thus also suggest that algorithm unrolling models are prone to overfitting as the unrolling depth $D'$ increases. We provide several examples to illustrate these results.

On Bayesian sparse canonical correlation analysis via Rayleigh quotient framework

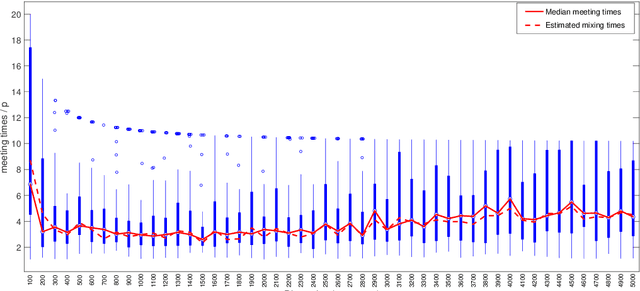
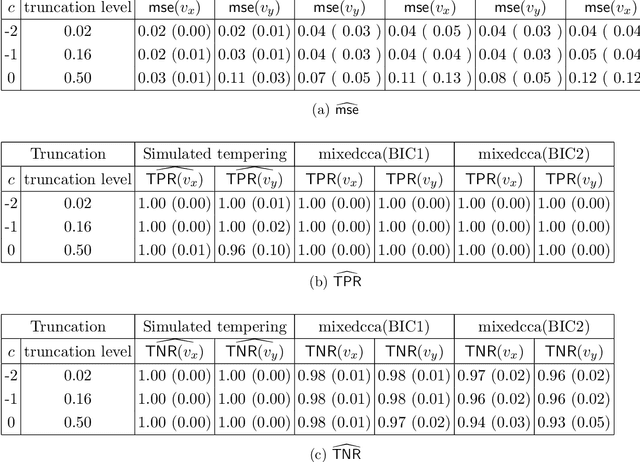
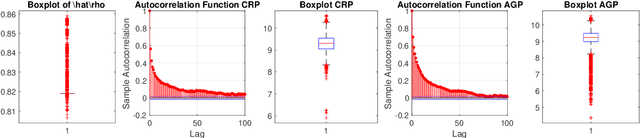
We propose a semi-parametric Bayesian method for the principal canonical pair that employs the scaled Rayleigh quotient as a quasi-log-likelihood with the spike-and-slab prior as the sparse constraints. Our approach does not require a complete joint distribution of the data, and as such, is more robust to non-normality than current Bayesian methods. Moreover, simulated tempering is used for solving the multi-modality problem in the resulting posterior distribution. We study the numerical behavior of the proposed method on both continuous and truncated data, and show that it compares favorably with other methods. As an application, we use the methodology to maximally correlate clinical variables and proteomic data for a better understanding of covid-19 disease. Our analysis identifies the protein Alpha-1-acid glycoprotein 1 (AGP 1) as playing an important role in the progression of Covid-19 into a severe illness.

Sequential change-point detection in high-dimensional Gaussian graphical models

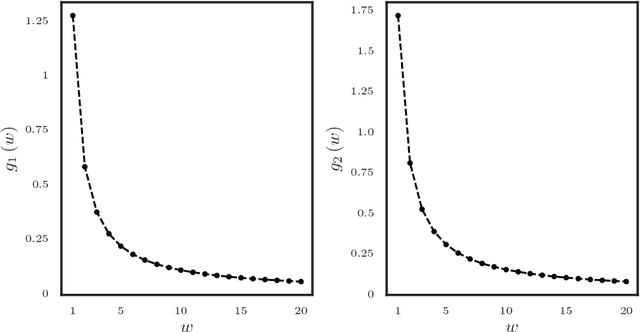
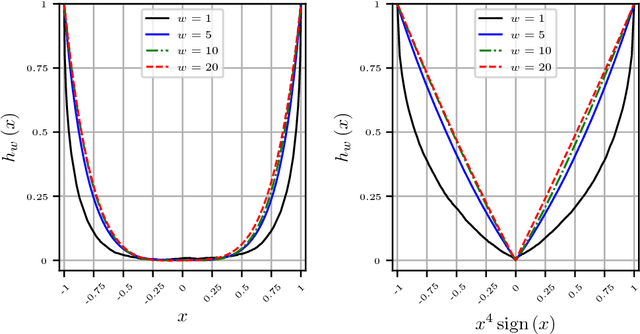
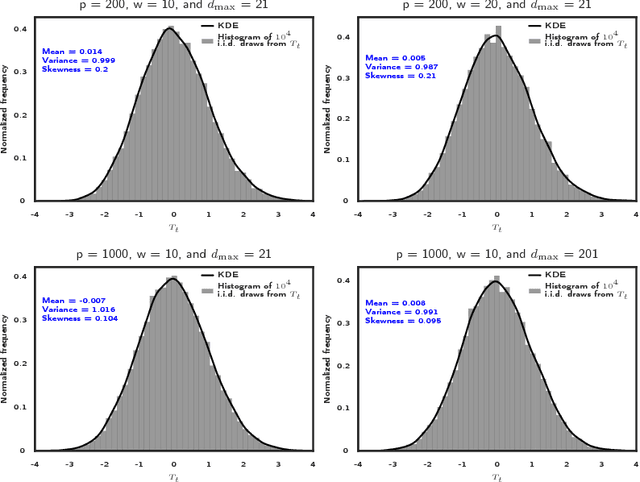
High dimensional piecewise stationary graphical models represent a versatile class for modelling time varying networks arising in diverse application areas, including biology, economics, and social sciences. There has been recent work in offline detection and estimation of regime changes in the topology of sparse graphical models. However, the online setting remains largely unexplored, despite its high relevance to applications in sensor networks and other engineering monitoring systems, as well as financial markets. To that end, this work introduces a novel scalable online algorithm for detecting an unknown number of abrupt changes in the inverse covariance matrix of sparse Gaussian graphical models with small delay. The proposed algorithm is based upon monitoring the conditional log-likelihood of all nodes in the network and can be extended to a large class of continuous and discrete graphical models. We also investigate asymptotic properties of our procedure under certain mild regularity conditions on the graph size, sparsity level, number of samples, and pre- and post-changes in the topology of the network. Numerical works on both synthetic and real data illustrate the good performance of the proposed methodology both in terms of computational and statistical efficiency across numerous experimental settings.