On Bayesian sparse canonical correlation analysis via Rayleigh quotient framework

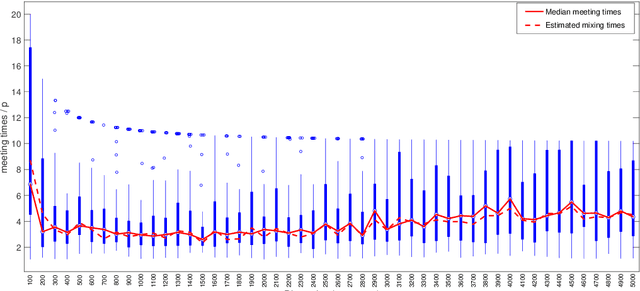
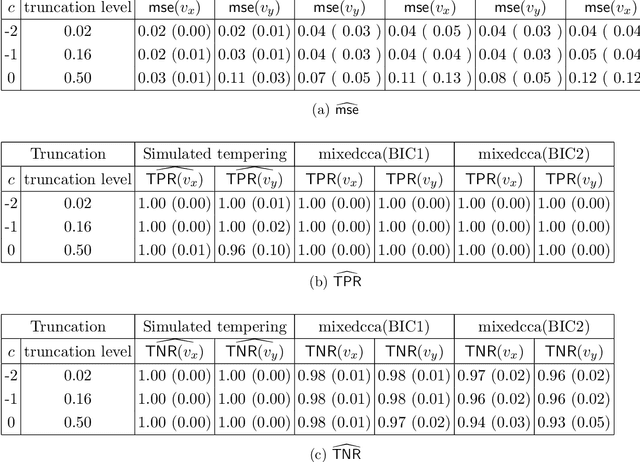
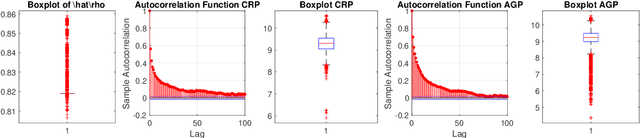
We propose a semi-parametric Bayesian method for the principal canonical pair that employs the scaled Rayleigh quotient as a quasi-log-likelihood with the spike-and-slab prior as the sparse constraints. Our approach does not require a complete joint distribution of the data, and as such, is more robust to non-normality than current Bayesian methods. Moreover, simulated tempering is used for solving the multi-modality problem in the resulting posterior distribution. We study the numerical behavior of the proposed method on both continuous and truncated data, and show that it compares favorably with other methods. As an application, we use the methodology to maximally correlate clinical variables and proteomic data for a better understanding of covid-19 disease. Our analysis identifies the protein Alpha-1-acid glycoprotein 1 (AGP 1) as playing an important role in the progression of Covid-19 into a severe illness.