A statistical perspective on algorithm unrolling models for inverse problems

We consider inverse problems where the conditional distribution of the observation ${\bf y}$ given the latent variable of interest ${\bf x}$ (also known as the forward model) is known, and we have access to a data set in which multiple instances of ${\bf x}$ and ${\bf y}$ are both observed. In this context, algorithm unrolling has become a very popular approach for designing state-of-the-art deep neural network architectures that effectively exploit the forward model. We analyze the statistical complexity of the gradient descent network (GDN), an algorithm unrolling architecture driven by proximal gradient descent. We show that the unrolling depth needed for the optimal statistical performance of GDNs is of order $\log(n)/\log(\varrho_n^{-1})$, where $n$ is the sample size, and $\varrho_n$ is the convergence rate of the corresponding gradient descent algorithm. We also show that when the negative log-density of the latent variable ${\bf x}$ has a simple proximal operator, then a GDN unrolled at depth $D'$ can solve the inverse problem at the parametric rate $O(D'/\sqrt{n})$. Our results thus also suggest that algorithm unrolling models are prone to overfitting as the unrolling depth $D'$ increases. We provide several examples to illustrate these results.

On Bayesian sparse canonical correlation analysis via Rayleigh quotient framework

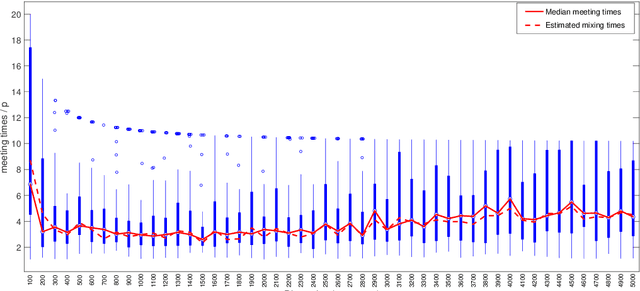
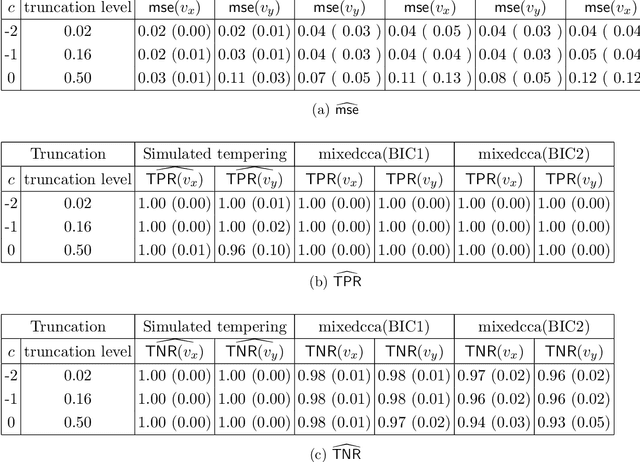
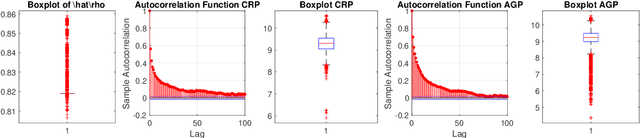
We propose a semi-parametric Bayesian method for the principal canonical pair that employs the scaled Rayleigh quotient as a quasi-log-likelihood with the spike-and-slab prior as the sparse constraints. Our approach does not require a complete joint distribution of the data, and as such, is more robust to non-normality than current Bayesian methods. Moreover, simulated tempering is used for solving the multi-modality problem in the resulting posterior distribution. We study the numerical behavior of the proposed method on both continuous and truncated data, and show that it compares favorably with other methods. As an application, we use the methodology to maximally correlate clinical variables and proteomic data for a better understanding of covid-19 disease. Our analysis identifies the protein Alpha-1-acid glycoprotein 1 (AGP 1) as playing an important role in the progression of Covid-19 into a severe illness.