ApacheJIT: A Large Dataset for Just-In-Time Defect Prediction

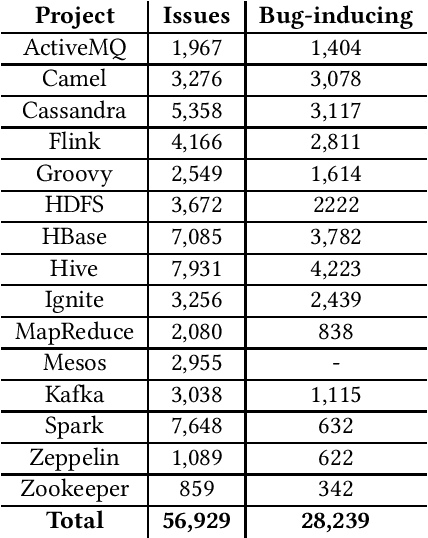
In this paper, we present ApacheJIT, a large dataset for Just-In-Time defect prediction. ApacheJIT consists of clean and bug-inducing software changes in popular Apache projects. ApacheJIT has a total of 106,674 commits (28,239 bug-inducing and 78,435 clean commits). Having a large number of commits makes ApacheJIT a suitable dataset for machine learning models, especially deep learning models that require large training sets to effectively generalize the patterns present in the historical data to future data. In addition to the original dataset, we also present carefully selected training and test sets that we recommend to be used in training and evaluating machine learning models.

SURENA IV: Towards A Cost-effective Full-size Humanoid Robot for Real-world Scenarios

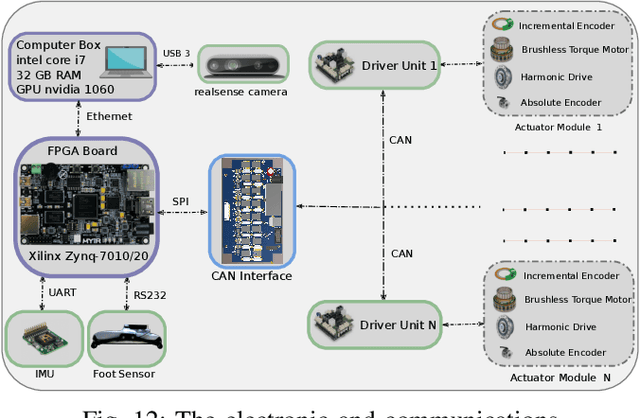
This paper describes the hardware, software framework, and experimental testing of SURENA IV humanoid robotics platform. SURENA IV has 43 degrees of freedom (DoFs), including seven DoFs for each arm, six DoFs for each hand, and six DoFs for each leg, with a height of 170 cm and a mass of 68 kg and morphological and mass properties similar to an average adult human. SURENA IV aims to realize a cost-effective and anthropomorphic humanoid robot for real-world scenarios. In this way, we demonstrate a locomotion framework based on a novel and inexpensive predictive foot sensor that enables walking with 7cm foot position error because of accumulative error of links and connections' deflection(that has been manufactured by the tools which are available in the Universities). Thanks to this sensor, the robot can walk on unknown obstacles without any force feedback, by online adaptation of foot height and orientation. Moreover, the arm and hand of the robot have been designed to grasp the objects with different stiffness and geometries that enable the robot to do drilling, visual servoing of a moving object, and writing his name on the white-board.

Online detection of local abrupt changes in high-dimensional Gaussian graphical models

The problem of identifying change points in high-dimensional Gaussian graphical models (GGMs) in an online fashion is of interest, due to new applications in biology, economics and social sciences. The offline version of the problem, where all the data are a priori available, has led to a number of methods and associated algorithms involving regularized loss functions. However, for the online version, there is currently only a single work in the literature that develops a sequential testing procedure and also studies its asymptotic false alarm probability and power. The latter test is best suited for the detection of change points driven by global changes in the structure of the precision matrix of the GGM, in the sense that many edges are involved. Nevertheless, in many practical settings the change point is driven by local changes, in the sense that only a small number of edges exhibit changes. To that end, we develop a novel test to address this problem that is based on the $\ell_\infty$ norm of the normalized covariance matrix of an appropriately selected portion of incoming data. The study of the asymptotic distribution of the proposed test statistic under the null (no presence of a change point) and the alternative (presence of a change point) hypotheses requires new technical tools that examine maxima of graph-dependent Gaussian random variables, and that of independent interest. It is further shown that these tools lead to the imposition of mild regularity conditions for key model parameters, instead of more stringent ones required by leveraging previously used tools in related problems in the literature. Numerical work on synthetic data illustrates the good performance of the proposed detection procedure both in terms of computational and statistical efficiency across numerous experimental settings.

A Deep Learning-Based Approach for Measuring the Domain Similarity of Persian Texts

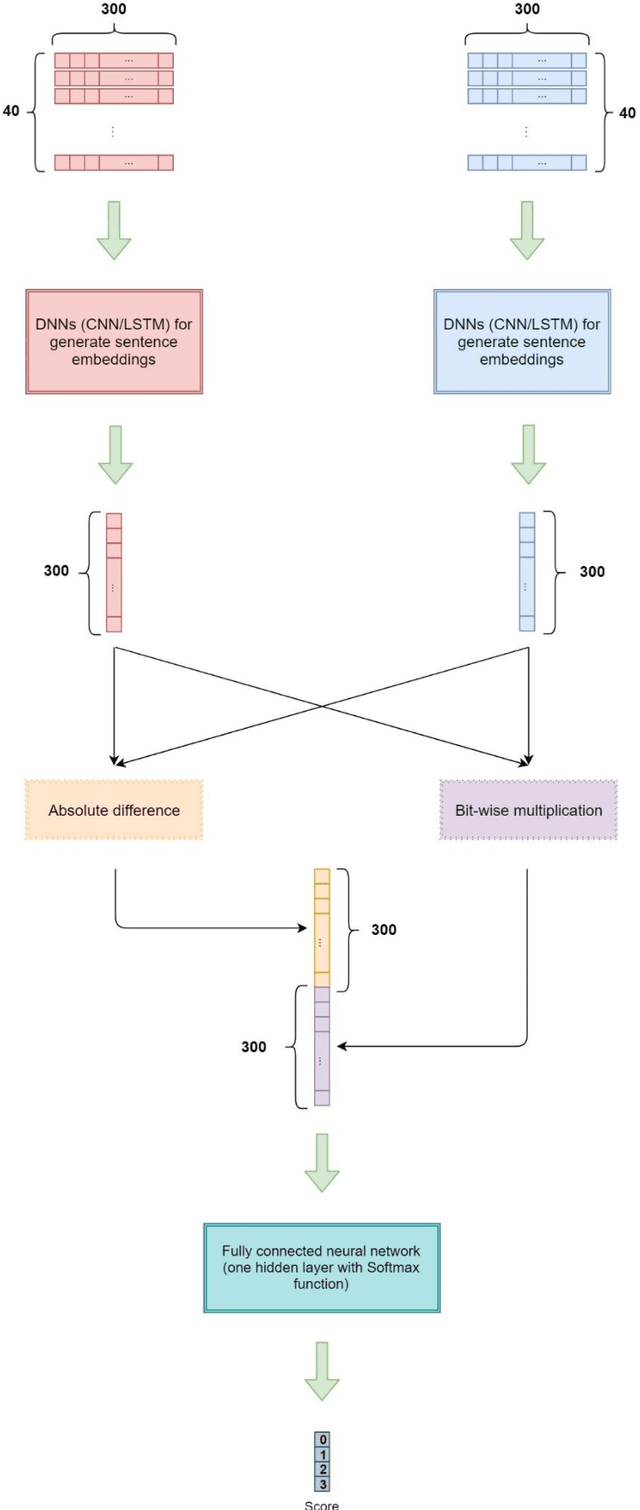
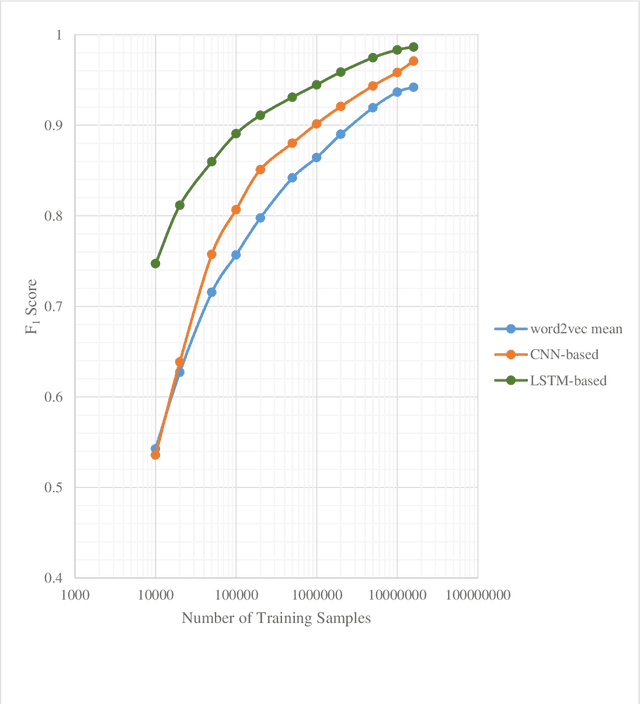
In this paper, we propose a novel approach for measuring the degree of similarity between categories of two pieces of Persian text, which were published as descriptions of two separate advertisements. We built an appropriate dataset for this work using a dataset which consists of advertisements posted on an e-commerce website. We generated a significant number of paired texts from this dataset and assigned each pair a score from 0 to 3, which demonstrates the degree of similarity between the domains of the pair. In this work, we represent words with word embedding vectors derived from word2vec. Then deep neural network models are used to represent texts. Eventually, we employ concatenation of absolute difference and bit-wise multiplication and a fully-connected neural network to produce a probability distribution vector for the score of the pairs. Through a supervised learning approach, we trained our model on a GPU, and our best model achieved an F1 score of 0.9865.

Sequential change-point detection in high-dimensional Gaussian graphical models

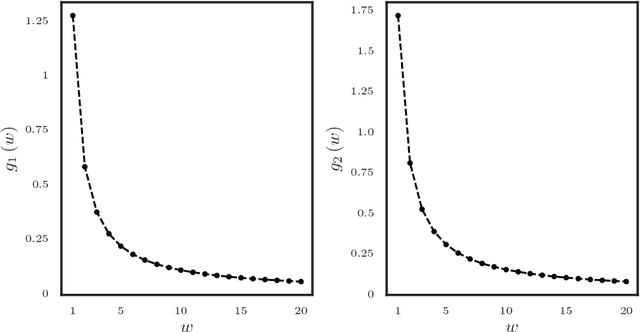
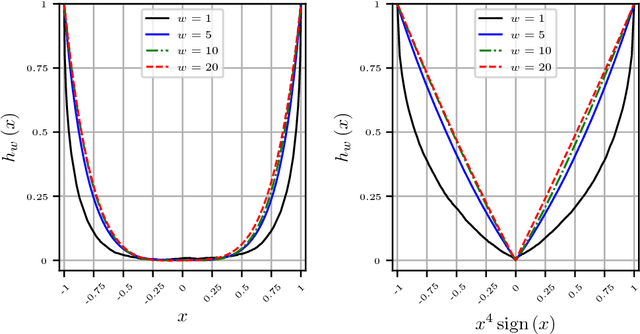
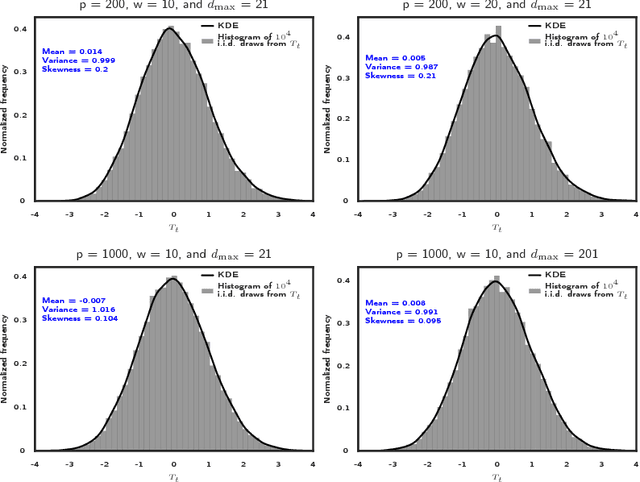
High dimensional piecewise stationary graphical models represent a versatile class for modelling time varying networks arising in diverse application areas, including biology, economics, and social sciences. There has been recent work in offline detection and estimation of regime changes in the topology of sparse graphical models. However, the online setting remains largely unexplored, despite its high relevance to applications in sensor networks and other engineering monitoring systems, as well as financial markets. To that end, this work introduces a novel scalable online algorithm for detecting an unknown number of abrupt changes in the inverse covariance matrix of sparse Gaussian graphical models with small delay. The proposed algorithm is based upon monitoring the conditional log-likelihood of all nodes in the network and can be extended to a large class of continuous and discrete graphical models. We also investigate asymptotic properties of our procedure under certain mild regularity conditions on the graph size, sparsity level, number of samples, and pre- and post-changes in the topology of the network. Numerical works on both synthetic and real data illustrate the good performance of the proposed methodology both in terms of computational and statistical efficiency across numerous experimental settings.

Optimal change point detection in Gaussian processes

We study the problem of detecting a change in the mean of one-dimensional Gaussian process data. This problem is investigated in the setting of increasing domain (customarily employed in time series analysis) and in the setting of fixed domain (typically arising in spatial data analysis). We propose a detection method based on the generalized likelihood ratio test (GLRT), and show that our method achieves nearly asymptotically optimal rate in the minimax sense, in both settings. The salient feature of the proposed method is that it exploits in an efficient way the data dependence captured by the Gaussian process covariance structure. When the covariance is not known, we propose the plug-in GLRT method and derive conditions under which the method remains asymptotically near optimal. By contrast, the standard CUSUM method, which does not account for the covariance structure, is shown to be asymptotically optimal only in the increasing domain. Our algorithms and accompanying theory are applicable to a wide variety of covariance structures, including the Matern class, the powered exponential class, and others. The plug-in GLRT method is shown to perform well for maximum likelihood estimators with a dense covariance matrix.

On the consistency of inversion-free parameter estimation for Gaussian random fields

Gaussian random fields are a powerful tool for modeling environmental processes. For high dimensional samples, classical approaches for estimating the covariance parameters require highly challenging and massive computations, such as the evaluation of the Cholesky factorization or solving linear systems. Recently, Anitescu, Chen and Stein \cite{M.Anitescu} proposed a fast and scalable algorithm which does not need such burdensome computations. The main focus of this article is to study the asymptotic behavior of the algorithm of Anitescu et al. (ACS) for regular and irregular grids in the increasing domain setting. Consistency, minimax optimality and asymptotic normality of this algorithm are proved under mild differentiability conditions on the covariance function. Despite the fact that ACS's method entails a non-concave maximization, our results hold for any stationary point of the objective function. A numerical study is presented to evaluate the efficiency of this algorithm for large data sets.