Convolutional Differentiable Logic Gate Networks

With the increasing inference cost of machine learning models, there is a growing interest in models with fast and efficient inference. Recently, an approach for learning logic gate networks directly via a differentiable relaxation was proposed. Logic gate networks are faster than conventional neural network approaches because their inference only requires logic gate operators such as NAND, OR, and XOR, which are the underlying building blocks of current hardware and can be efficiently executed. We build on this idea, extending it by deep logic gate tree convolutions, logical OR pooling, and residual initializations. This allows scaling logic gate networks up by over one order of magnitude and utilizing the paradigm of convolution. On CIFAR-10, we achieve an accuracy of 86.29% using only 61 million logic gates, which improves over the SOTA while being 29x smaller.

TrAct: Making First-layer Pre-Activations Trainable

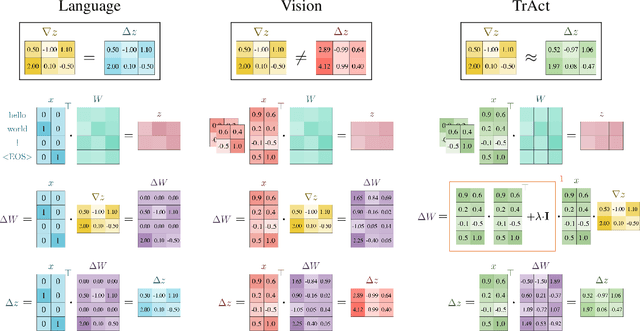
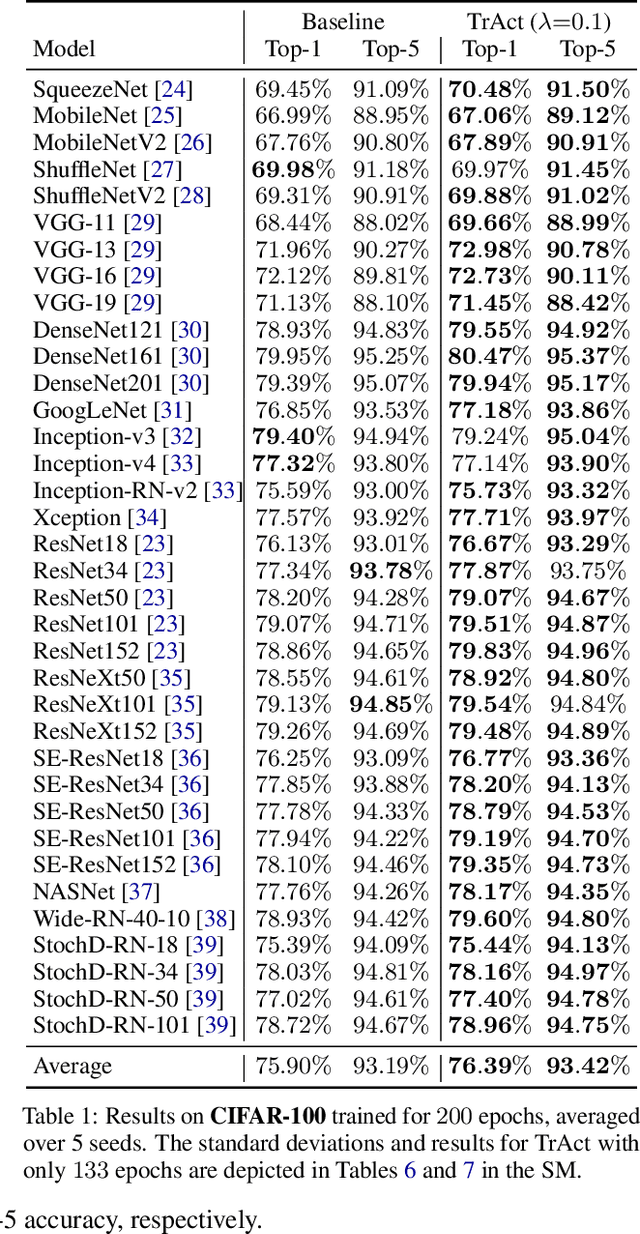
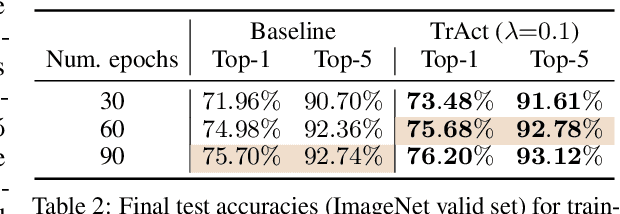
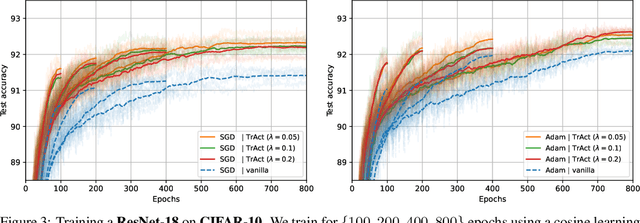
We consider the training of the first layer of vision models and notice the clear relationship between pixel values and gradient update magnitudes: the gradients arriving at the weights of a first layer are by definition directly proportional to (normalized) input pixel values. Thus, an image with low contrast has a smaller impact on learning than an image with higher contrast, and a very bright or very dark image has a stronger impact on the weights than an image with moderate brightness. In this work, we propose performing gradient descent on the embeddings produced by the first layer of the model. However, switching to discrete inputs with an embedding layer is not a reasonable option for vision models. Thus, we propose the conceptual procedure of (i) a gradient descent step on first layer activations to construct an activation proposal, and (ii) finding the optimal weights of the first layer, i.e., those weights which minimize the squared distance to the activation proposal. We provide a closed form solution of the procedure and adjust it for robust stochastic training while computing everything efficiently. Empirically, we find that TrAct (Training Activations) speeds up training by factors between 1.25x and 4x while requiring only a small computational overhead. We demonstrate the utility of TrAct with different optimizers for a range of different vision models including convolutional and transformer architectures.

Newton Losses: Using Curvature Information for Learning with Differentiable Algorithms

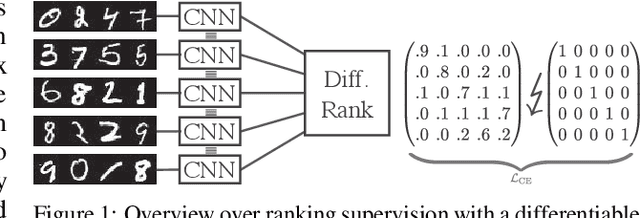
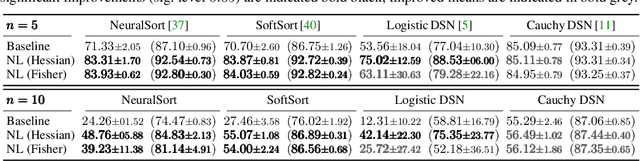
When training neural networks with custom objectives, such as ranking losses and shortest-path losses, a common problem is that they are, per se, non-differentiable. A popular approach is to continuously relax the objectives to provide gradients, enabling learning. However, such differentiable relaxations are often non-convex and can exhibit vanishing and exploding gradients, making them (already in isolation) hard to optimize. Here, the loss function poses the bottleneck when training a deep neural network. We present Newton Losses, a method for improving the performance of existing hard to optimize losses by exploiting their second-order information via their empirical Fisher and Hessian matrices. Instead of training the neural network with second-order techniques, we only utilize the loss function's second-order information to replace it by a Newton Loss, while training the network with gradient descent. This makes our method computationally efficient. We apply Newton Losses to eight differentiable algorithms for sorting and shortest-paths, achieving significant improvements for less-optimized differentiable algorithms, and consistent improvements, even for well-optimized differentiable algorithms.

Generalizing Stochastic Smoothing for Differentiation and Gradient Estimation

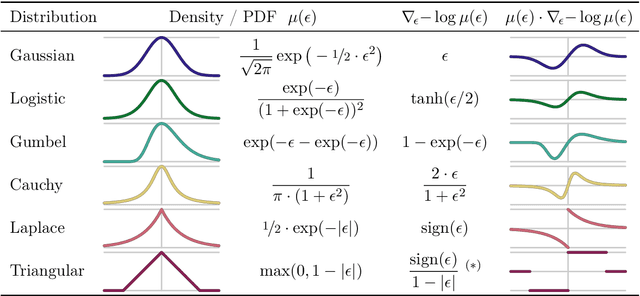
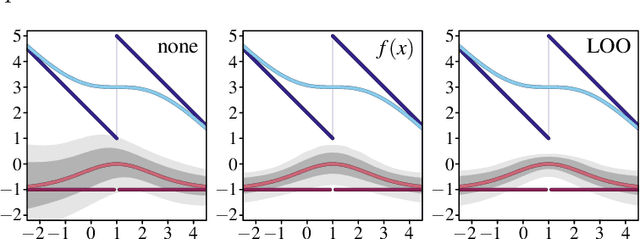
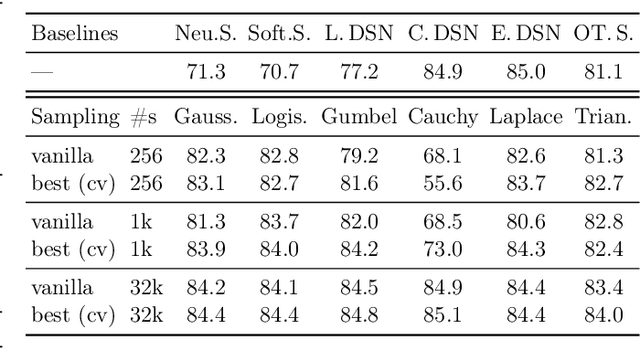
We deal with the problem of gradient estimation for stochastic differentiable relaxations of algorithms, operators, simulators, and other non-differentiable functions. Stochastic smoothing conventionally perturbs the input of a non-differentiable function with a differentiable density distribution with full support, smoothing it and enabling gradient estimation. Our theory starts at first principles to derive stochastic smoothing with reduced assumptions, without requiring a differentiable density nor full support, and we present a general framework for relaxation and gradient estimation of non-differentiable black-box functions $f:\mathbb{R}^n\to\mathbb{R}^m$. We develop variance reduction for gradient estimation from 3 orthogonal perspectives. Empirically, we benchmark 6 distributions and up to 24 variance reduction strategies for differentiable sorting and ranking, differentiable shortest-paths on graphs, differentiable rendering for pose estimation, as well as differentiable cryo-ET simulations.

CPSample: Classifier Protected Sampling for Guarding Training Data During Diffusion

Diffusion models have a tendency to exactly replicate their training data, especially when trained on small datasets. Most prior work has sought to mitigate this problem by imposing differential privacy constraints or masking parts of the training data, resulting in a notable substantial decrease in image quality. We present CPSample, a method that modifies the sampling process to prevent training data replication while preserving image quality. CPSample utilizes a classifier that is trained to overfit on random binary labels attached to the training data. CPSample then uses classifier guidance to steer the generation process away from the set of points that can be classified with high certainty, a set that includes the training data. CPSample achieves FID scores of 4.97 and 2.97 on CIFAR-10 and CelebA-64, respectively, without producing exact replicates of the training data. Unlike prior methods intended to guard the training images, CPSample only requires training a classifier rather than retraining a diffusion model, which is computationally cheaper. Moreover, our technique provides diffusion models with greater robustness against membership inference attacks, wherein an adversary attempts to discern which images were in the model's training dataset. We show that CPSample behaves like a built-in rejection sampler, and we demonstrate its capabilities to prevent mode collapse in Stable Diffusion.

Uncertainty Quantification via Stable Distribution Propagation

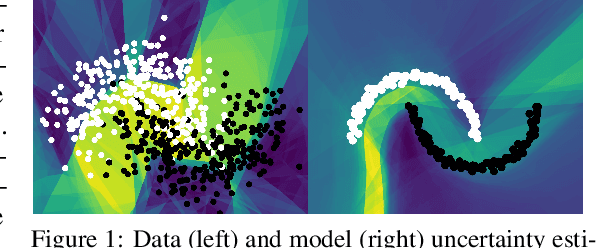
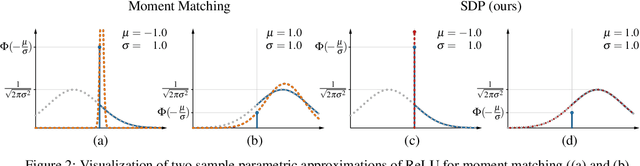
We propose a new approach for propagating stable probability distributions through neural networks. Our method is based on local linearization, which we show to be an optimal approximation in terms of total variation distance for the ReLU non-linearity. This allows propagating Gaussian and Cauchy input uncertainties through neural networks to quantify their output uncertainties. To demonstrate the utility of propagating distributions, we apply the proposed method to predicting calibrated confidence intervals and selective prediction on out-of-distribution data. The results demonstrate a broad applicability of propagating distributions and show the advantages of our method over other approaches such as moment matching.

Grounding Everything: Emerging Localization Properties in Vision-Language Transformers

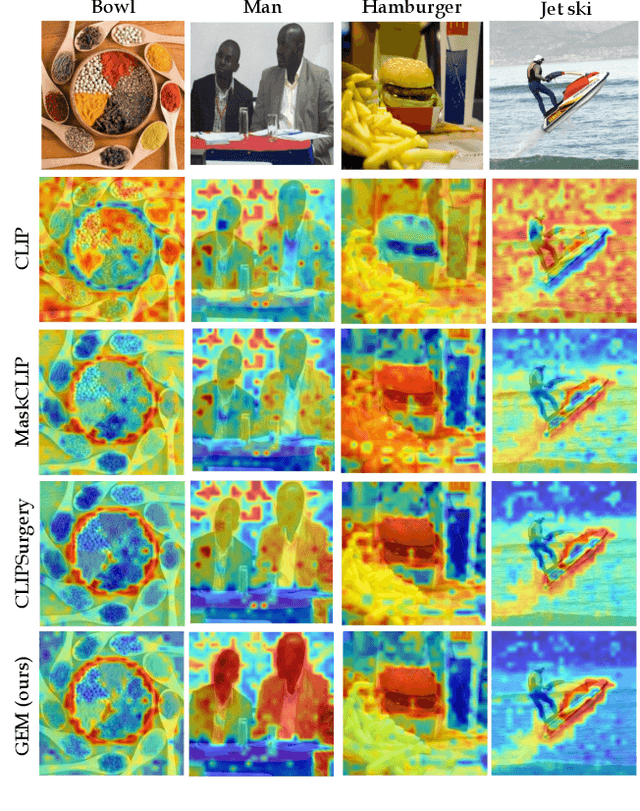
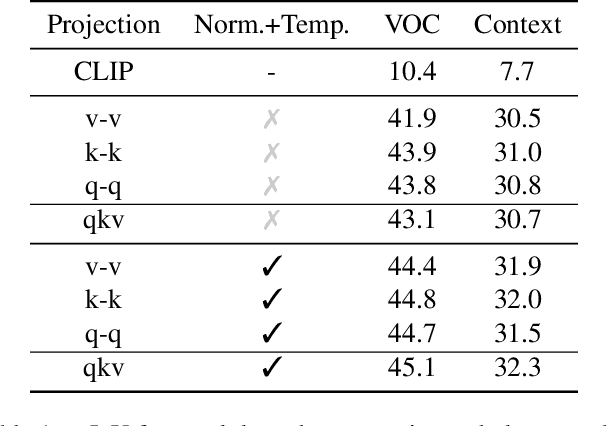
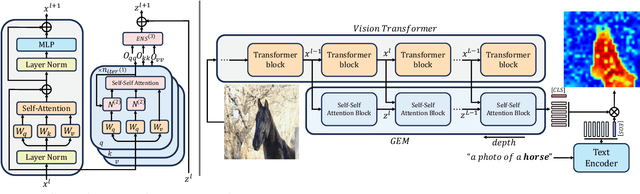
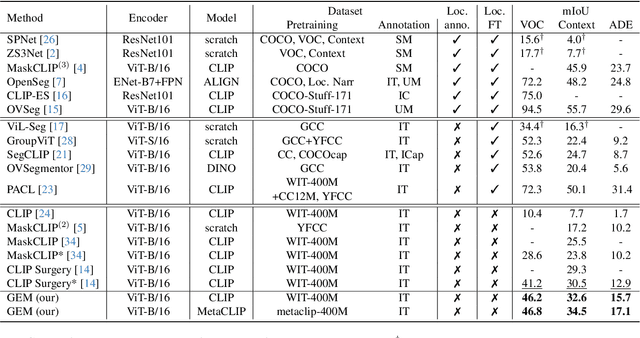
Vision-language foundation models have shown remarkable performance in various zero-shot settings such as image retrieval, classification, or captioning. But so far, those models seem to fall behind when it comes to zero-shot localization of referential expressions and objects in images. As a result, they need to be fine-tuned for this task. In this paper, we show that pretrained vision-language (VL) models allow for zero-shot open-vocabulary object localization without any fine-tuning. To leverage those capabilities, we propose a Grounding Everything Module (GEM) that generalizes the idea of value-value attention introduced by CLIPSurgery to a self-self attention path. We show that the concept of self-self attention corresponds to clustering, thus enforcing groups of tokens arising from the same object to be similar while preserving the alignment with the language space. To further guide the group formation, we propose a set of regularizations that allows the model to finally generalize across datasets and backbones. We evaluate the proposed GEM framework on various benchmark tasks and datasets for semantic segmentation. It shows that GEM not only outperforms other training-free open-vocabulary localization methods, but also achieves state-of-the-art results on the recently proposed OpenImagesV7 large-scale segmentation benchmark.

Neural Machine Translation for Mathematical Formulae

We tackle the problem of neural machine translation of mathematical formulae between ambiguous presentation languages and unambiguous content languages. Compared to neural machine translation on natural language, mathematical formulae have a much smaller vocabulary and much longer sequences of symbols, while their translation requires extreme precision to satisfy mathematical information needs. In this work, we perform the tasks of translating from LaTeX to Mathematica as well as from LaTeX to semantic LaTeX. While recurrent, recursive, and transformer networks struggle with preserving all contained information, we find that convolutional sequence-to-sequence networks achieve 95.1% and 90.7% exact matches, respectively.

ISAAC Newton: Input-based Approximate Curvature for Newton's Method

We present ISAAC (Input-baSed ApproximAte Curvature), a novel method that conditions the gradient using selected second-order information and has an asymptotically vanishing computational overhead, assuming a batch size smaller than the number of neurons. We show that it is possible to compute a good conditioner based on only the input to a respective layer without a substantial computational overhead. The proposed method allows effective training even in small-batch stochastic regimes, which makes it competitive to first-order as well as second-order methods.

Learning by Sorting: Self-supervised Learning with Group Ordering Constraints

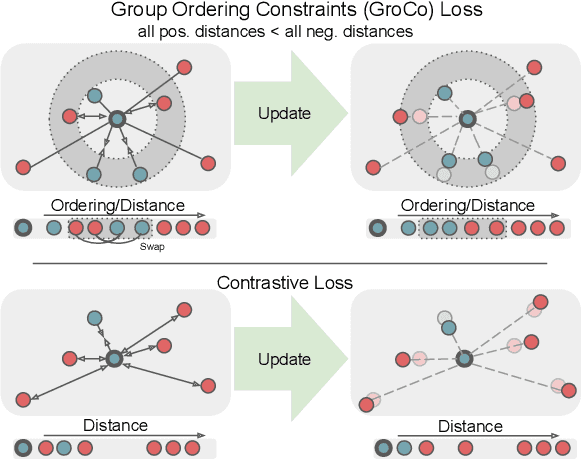
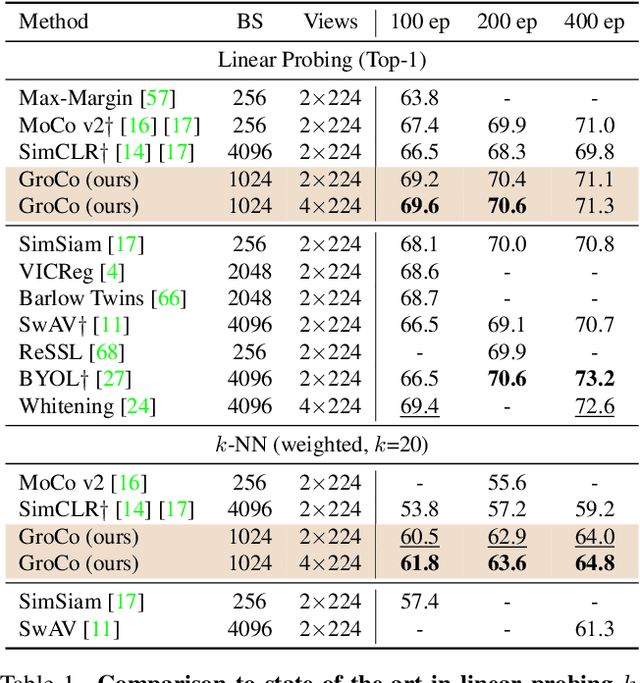
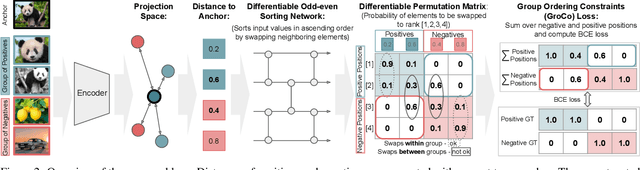
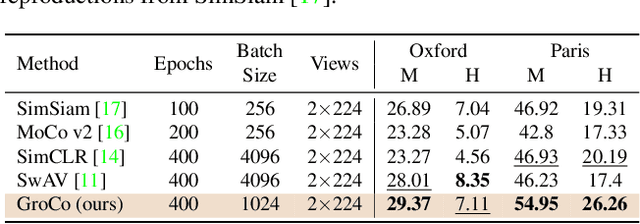
Contrastive learning has become a prominent ingredient in learning representations from unlabeled data. However, existing methods primarily consider pairwise relations. This paper proposes a new approach towards self-supervised contrastive learning based on Group Ordering Constraints (GroCo). The GroCo loss leverages the idea of comparing groups of positive and negative images instead of pairs of images. Building on the recent success of differentiable sorting algorithms, group ordering constraints enforce that the distances of all positive samples (a positive group) are smaller than the distances of all negative images (a negative group); thus, enforcing positive samples to gather around an anchor. This leads to a more holistic optimization of the local neighborhoods. We evaluate the proposed setting on a suite of competitive self-supervised learning benchmarks and show that our method is not only competitive to current methods in the case of linear probing but also leads to higher consistency in local representations, as can be seen from a significantly improved k-NN performance across all benchmarks.