Data Augmentation of Time-Series Data in Human Movement Biomechanics: A Scoping Review

The integration of machine learning and deep learning has transformed data analytics in biomechanics, enabled by extensive wearable sensor data. However, the field faces challenges such as limited large-scale datasets and high data acquisition costs, which hinder the development of robust algorithms. Data augmentation techniques show promise in addressing these issues, but their application to biomechanical time-series data requires comprehensive evaluation. This scoping review investigates data augmentation methods for time-series data in the biomechanics domain. It analyzes current approaches for augmenting and generating time-series datasets, evaluates their effectiveness, and offers recommendations for applying these techniques in biomechanics. Four databases, PubMed, IEEE Xplore, Scopus, and Web of Science, were searched for studies published between 2013 and 2024. Following PRISMA-ScR guidelines, a two-stage screening identified 21 relevant publications. Results show that there is no universally preferred method for augmenting biomechanical time-series data; instead, methods vary based on study objectives. A major issue identified is the absence of soft tissue artifacts in synthetic data, leading to discrepancies referred to as the synthetic gap. Moreover, many studies lack proper evaluation of augmentation methods, making it difficult to assess their effects on model performance and data quality. This review highlights the critical role of data augmentation in addressing limited dataset availability and improving model generalization in biomechanics. Tailoring augmentation strategies to the characteristics of biomechanical data is essential for advancing predictive modeling. A better understanding of how different augmentation methods impact data quality and downstream tasks will be key to developing more effective and realistic techniques.

Convolutional Differentiable Logic Gate Networks

With the increasing inference cost of machine learning models, there is a growing interest in models with fast and efficient inference. Recently, an approach for learning logic gate networks directly via a differentiable relaxation was proposed. Logic gate networks are faster than conventional neural network approaches because their inference only requires logic gate operators such as NAND, OR, and XOR, which are the underlying building blocks of current hardware and can be efficiently executed. We build on this idea, extending it by deep logic gate tree convolutions, logical OR pooling, and residual initializations. This allows scaling logic gate networks up by over one order of magnitude and utilizing the paradigm of convolution. On CIFAR-10, we achieve an accuracy of 86.29% using only 61 million logic gates, which improves over the SOTA while being 29x smaller.

TrAct: Making First-layer Pre-Activations Trainable

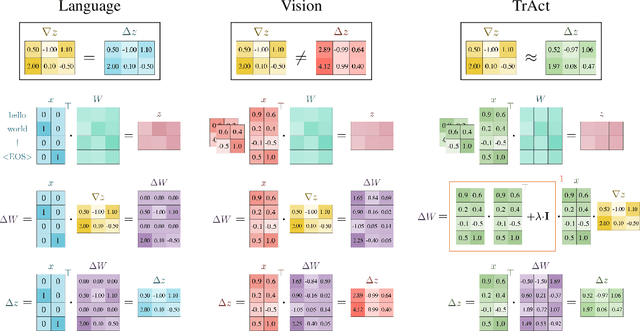
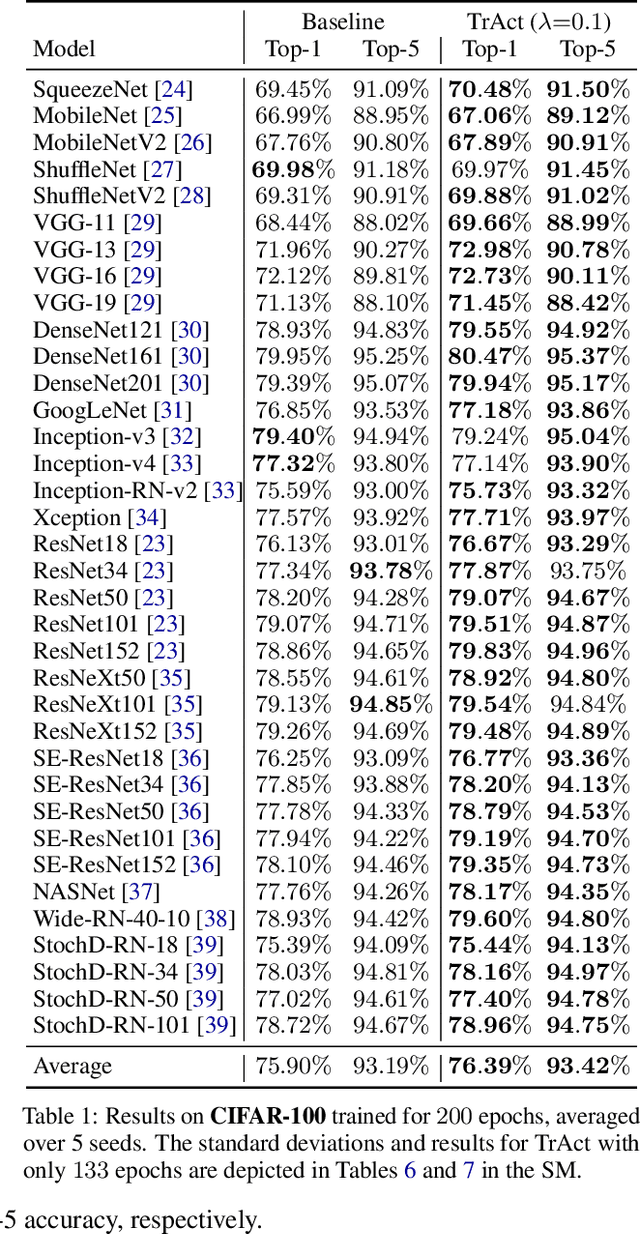
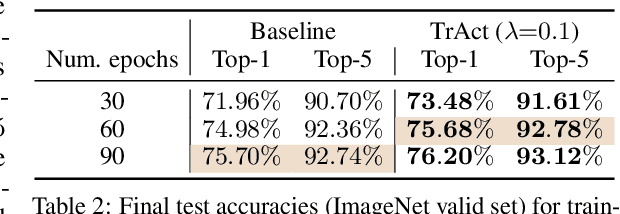
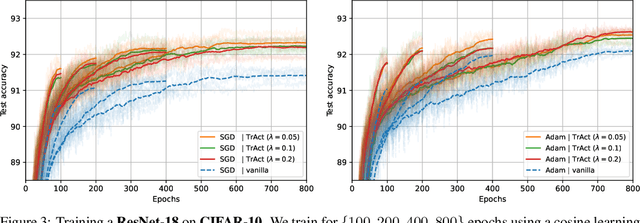
We consider the training of the first layer of vision models and notice the clear relationship between pixel values and gradient update magnitudes: the gradients arriving at the weights of a first layer are by definition directly proportional to (normalized) input pixel values. Thus, an image with low contrast has a smaller impact on learning than an image with higher contrast, and a very bright or very dark image has a stronger impact on the weights than an image with moderate brightness. In this work, we propose performing gradient descent on the embeddings produced by the first layer of the model. However, switching to discrete inputs with an embedding layer is not a reasonable option for vision models. Thus, we propose the conceptual procedure of (i) a gradient descent step on first layer activations to construct an activation proposal, and (ii) finding the optimal weights of the first layer, i.e., those weights which minimize the squared distance to the activation proposal. We provide a closed form solution of the procedure and adjust it for robust stochastic training while computing everything efficiently. Empirically, we find that TrAct (Training Activations) speeds up training by factors between 1.25x and 4x while requiring only a small computational overhead. We demonstrate the utility of TrAct with different optimizers for a range of different vision models including convolutional and transformer architectures.

Newton Losses: Using Curvature Information for Learning with Differentiable Algorithms

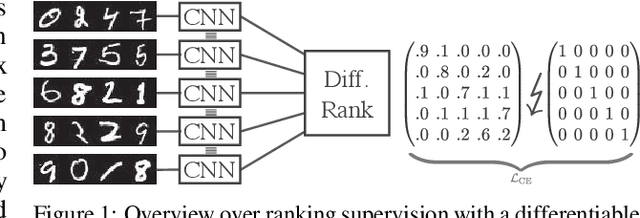
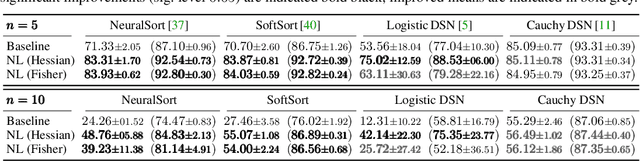
When training neural networks with custom objectives, such as ranking losses and shortest-path losses, a common problem is that they are, per se, non-differentiable. A popular approach is to continuously relax the objectives to provide gradients, enabling learning. However, such differentiable relaxations are often non-convex and can exhibit vanishing and exploding gradients, making them (already in isolation) hard to optimize. Here, the loss function poses the bottleneck when training a deep neural network. We present Newton Losses, a method for improving the performance of existing hard to optimize losses by exploiting their second-order information via their empirical Fisher and Hessian matrices. Instead of training the neural network with second-order techniques, we only utilize the loss function's second-order information to replace it by a Newton Loss, while training the network with gradient descent. This makes our method computationally efficient. We apply Newton Losses to eight differentiable algorithms for sorting and shortest-paths, achieving significant improvements for less-optimized differentiable algorithms, and consistent improvements, even for well-optimized differentiable algorithms.

Generalizing Stochastic Smoothing for Differentiation and Gradient Estimation

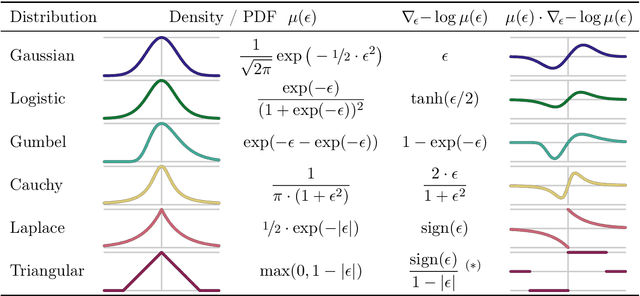
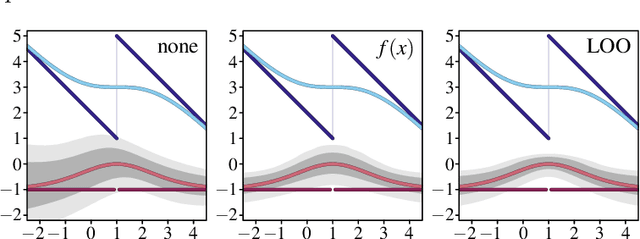
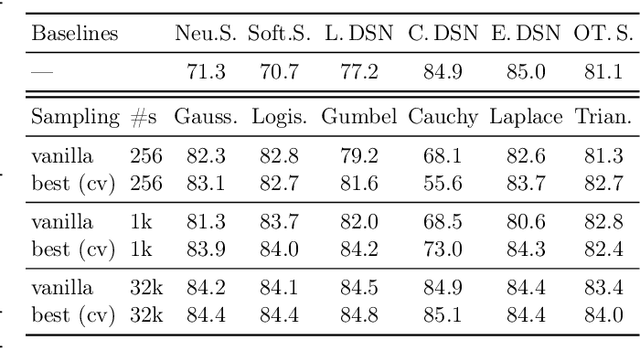
We deal with the problem of gradient estimation for stochastic differentiable relaxations of algorithms, operators, simulators, and other non-differentiable functions. Stochastic smoothing conventionally perturbs the input of a non-differentiable function with a differentiable density distribution with full support, smoothing it and enabling gradient estimation. Our theory starts at first principles to derive stochastic smoothing with reduced assumptions, without requiring a differentiable density nor full support, and we present a general framework for relaxation and gradient estimation of non-differentiable black-box functions $f:\mathbb{R}^n\to\mathbb{R}^m$. We develop variance reduction for gradient estimation from 3 orthogonal perspectives. Empirically, we benchmark 6 distributions and up to 24 variance reduction strategies for differentiable sorting and ranking, differentiable shortest-paths on graphs, differentiable rendering for pose estimation, as well as differentiable cryo-ET simulations.

Uncertainty Quantification via Stable Distribution Propagation

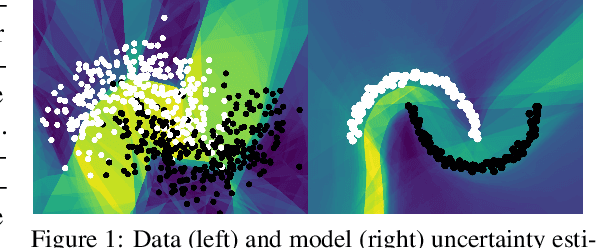
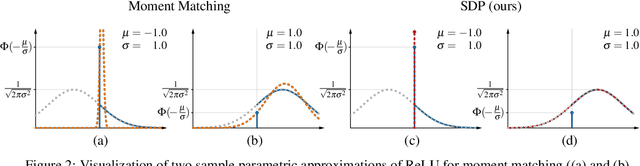
We propose a new approach for propagating stable probability distributions through neural networks. Our method is based on local linearization, which we show to be an optimal approximation in terms of total variation distance for the ReLU non-linearity. This allows propagating Gaussian and Cauchy input uncertainties through neural networks to quantify their output uncertainties. To demonstrate the utility of propagating distributions, we apply the proposed method to predicting calibrated confidence intervals and selective prediction on out-of-distribution data. The results demonstrate a broad applicability of propagating distributions and show the advantages of our method over other approaches such as moment matching.

ISAAC Newton: Input-based Approximate Curvature for Newton's Method

We present ISAAC (Input-baSed ApproximAte Curvature), a novel method that conditions the gradient using selected second-order information and has an asymptotically vanishing computational overhead, assuming a batch size smaller than the number of neurons. We show that it is possible to compute a good conditioner based on only the input to a respective layer without a substantial computational overhead. The proposed method allows effective training even in small-batch stochastic regimes, which makes it competitive to first-order as well as second-order methods.

Deep Differentiable Logic Gate Networks

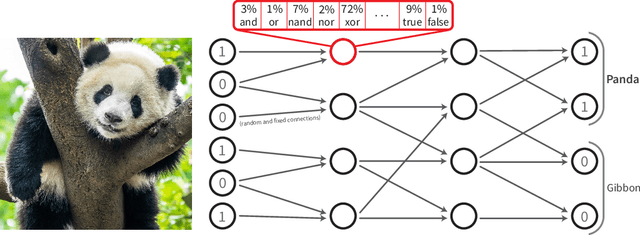
Recently, research has increasingly focused on developing efficient neural network architectures. In this work, we explore logic gate networks for machine learning tasks by learning combinations of logic gates. These networks comprise logic gates such as "AND" and "XOR", which allow for very fast execution. The difficulty in learning logic gate networks is that they are conventionally non-differentiable and therefore do not allow training with gradient descent. Thus, to allow for effective training, we propose differentiable logic gate networks, an architecture that combines real-valued logics and a continuously parameterized relaxation of the network. The resulting discretized logic gate networks achieve fast inference speeds, e.g., beyond a million images of MNIST per second on a single CPU core.

Differentiable Top-k Classification Learning

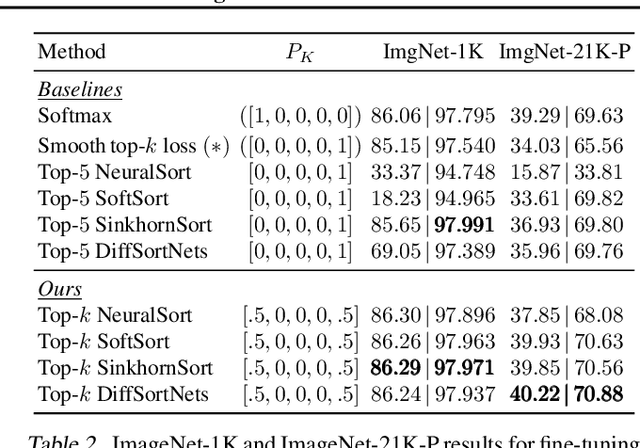
The top-k classification accuracy is one of the core metrics in machine learning. Here, k is conventionally a positive integer, such as 1 or 5, leading to top-1 or top-5 training objectives. In this work, we relax this assumption and optimize the model for multiple k simultaneously instead of using a single k. Leveraging recent advances in differentiable sorting and ranking, we propose a differentiable top-k cross-entropy classification loss. This allows training the network while not only considering the top-1 prediction, but also, e.g., the top-2 and top-5 predictions. We evaluate the proposed loss function for fine-tuning on state-of-the-art architectures, as well as for training from scratch. We find that relaxing k does not only produce better top-5 accuracies, but also leads to top-1 accuracy improvements. When fine-tuning publicly available ImageNet models, we achieve a new state-of-the-art for these models.

GenDR: A Generalized Differentiable Renderer

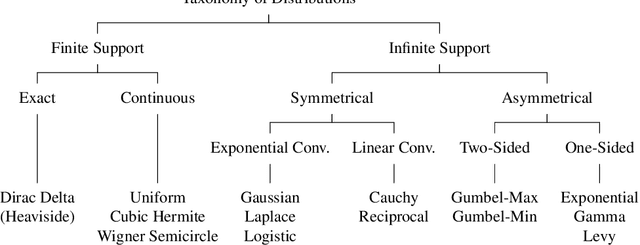
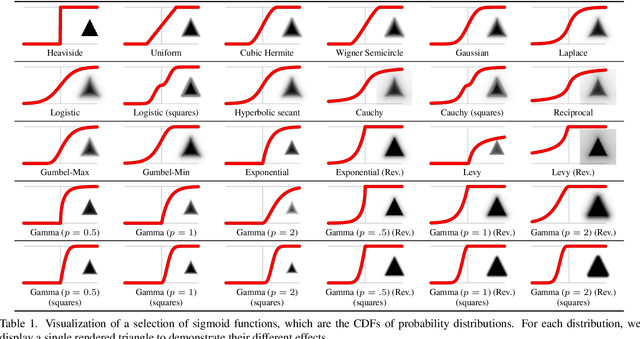
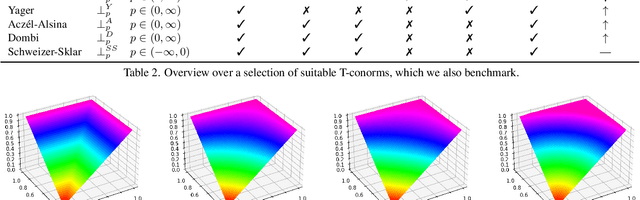
In this work, we present and study a generalized family of differentiable renderers. We discuss from scratch which components are necessary for differentiable rendering and formalize the requirements for each component. We instantiate our general differentiable renderer, which generalizes existing differentiable renderers like SoftRas and DIB-R, with an array of different smoothing distributions to cover a large spectrum of reasonable settings. We evaluate an array of differentiable renderer instantiations on the popular ShapeNet 3D reconstruction benchmark and analyze the implications of our results. Surprisingly, the simple uniform distribution yields the best overall results when averaged over 13 classes; in general, however, the optimal choice of distribution heavily depends on the task.