Deep Differentiable Logic Gate Networks
Paper and Code
Oct 15, 2022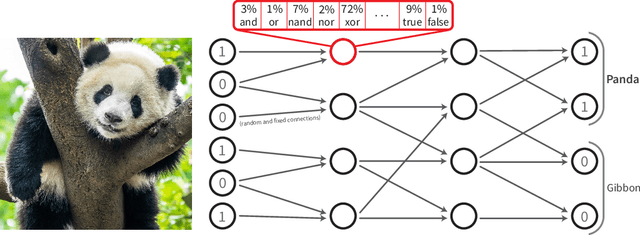



Recently, research has increasingly focused on developing efficient neural network architectures. In this work, we explore logic gate networks for machine learning tasks by learning combinations of logic gates. These networks comprise logic gates such as "AND" and "XOR", which allow for very fast execution. The difficulty in learning logic gate networks is that they are conventionally non-differentiable and therefore do not allow training with gradient descent. Thus, to allow for effective training, we propose differentiable logic gate networks, an architecture that combines real-valued logics and a continuously parameterized relaxation of the network. The resulting discretized logic gate networks achieve fast inference speeds, e.g., beyond a million images of MNIST per second on a single CPU core.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge