A Start To End Machine Learning Approach To Maximize Scientific Throughput From The LCLS-II-HE

With the increasing brightness of Light sources, including the Diffraction-Limited brightness upgrade of APS and the high-repetition-rate upgrade of LCLS, the proposed experiments therein are becoming increasingly complex. For instance, experiments at LCLS-II-HE will require the X-ray beam to be within a fraction of a micron in diameter, with pointing stability of a few nanoradians, at the end of a kilometer-long electron accelerator, a hundred-meter-long undulator section, and tens of meters long X-ray optics. This enhancement of brightness will increase the data production rate to rival the largest data generators in the world. Without real-time active feedback control and an optimized pipeline to transform measurements to scientific information and insights, researchers will drown in a deluge of mostly useless data, and fail to extract the highly sophisticated insights that the recent brightness upgrades promise. In this article, we outline the strategy we are developing at SLAC to implement Machine Learning driven optimization, automation and real-time knowledge extraction from the electron-injector at the start of the electron accelerator, to the multidimensional X-ray optical systems, and till the experimental endstations and the high readout rate, multi-megapixel detectors at LCLS to deliver the design performance to the users. This is illustrated via examples from Accelerator, Optics and End User applications.

Generalizing Stochastic Smoothing for Differentiation and Gradient Estimation

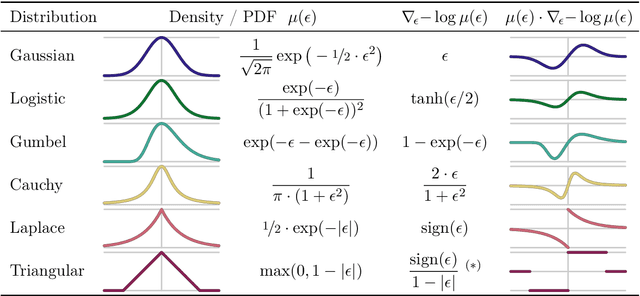
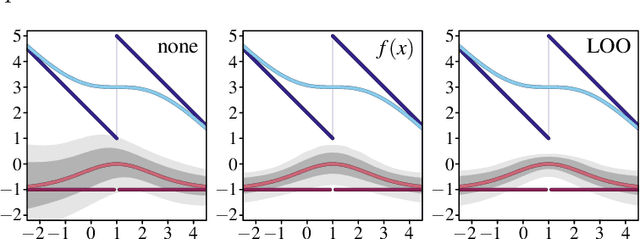
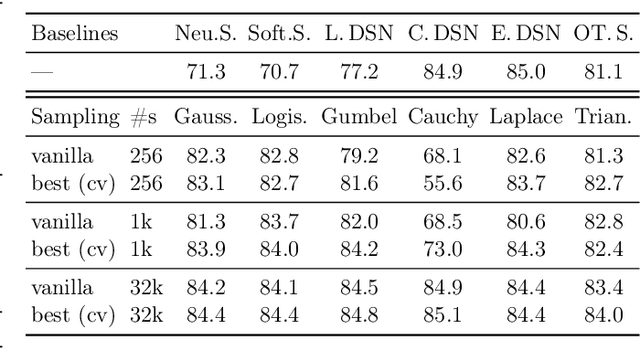
We deal with the problem of gradient estimation for stochastic differentiable relaxations of algorithms, operators, simulators, and other non-differentiable functions. Stochastic smoothing conventionally perturbs the input of a non-differentiable function with a differentiable density distribution with full support, smoothing it and enabling gradient estimation. Our theory starts at first principles to derive stochastic smoothing with reduced assumptions, without requiring a differentiable density nor full support, and we present a general framework for relaxation and gradient estimation of non-differentiable black-box functions $f:\mathbb{R}^n\to\mathbb{R}^m$. We develop variance reduction for gradient estimation from 3 orthogonal perspectives. Empirically, we benchmark 6 distributions and up to 24 variance reduction strategies for differentiable sorting and ranking, differentiable shortest-paths on graphs, differentiable rendering for pose estimation, as well as differentiable cryo-ET simulations.

Uncertainty Quantification via Stable Distribution Propagation

We propose a new approach for propagating stable probability distributions through neural networks. Our method is based on local linearization, which we show to be an optimal approximation in terms of total variation distance for the ReLU non-linearity. This allows propagating Gaussian and Cauchy input uncertainties through neural networks to quantify their output uncertainties. To demonstrate the utility of propagating distributions, we apply the proposed method to predicting calibrated confidence intervals and selective prediction on out-of-distribution data. The results demonstrate a broad applicability of propagating distributions and show the advantages of our method over other approaches such as moment matching.