BM$^2$: Coupled Schrödinger Bridge Matching

A Schr\"{o}dinger bridge establishes a dynamic transport map between two target distributions via a reference process, simultaneously solving an associated entropic optimal transport problem. We consider the setting where samples from the target distributions are available, and the reference diffusion process admits tractable dynamics. We thus introduce Coupled Bridge Matching (BM$^2$), a simple \emph{non-iterative} approach for learning Schr\"{o}dinger bridges with neural networks. A preliminary theoretical analysis of the convergence properties of BM$^2$ is carried out, supported by numerical experiments that demonstrate the effectiveness of our proposal.

Non-Denoising Forward-Time Diffusions

The scope of this paper is generative modeling through diffusion processes. An approach falling within this paradigm is the work of Song et al. (2021), which relies on a time-reversal argument to construct a diffusion process targeting the desired data distribution. We show that the time-reversal argument, common to all denoising diffusion probabilistic modeling proposals, is not necessary. We obtain diffusion processes targeting the desired data distribution by taking appropriate mixtures of diffusion bridges. The resulting transport is exact by construction, allows for greater flexibility in choosing the dynamics of the underlying diffusion, and can be approximated by means of a neural network via novel training objectives. We develop a unifying view of the drift adjustments corresponding to our and to time-reversal approaches and make use of this representation to inspect the inner workings of diffusion-based generative models. Finally, we leverage on scalable simulation and inference techniques common in spatial statistics to move beyond fully factorial distributions in the underlying diffusion dynamics. The methodological advances contained in this work contribute toward establishing a general framework for generative modeling based on diffusion processes.

Diffusion Bridge Mixture Transports, Schrödinger Bridge Problems and Generative Modeling

The dynamic Schr\"odinger bridge problem seeks a stochastic process that defines a transport between two target probability measures, while optimally satisfying the criteria of being closest, in terms of Kullback-Leibler divergence, to a reference process. We propose a novel sampling-based iterative algorithm, the iterated diffusion bridge mixture transport (IDBM), aimed at solving the dynamic Schr\"odinger bridge problem. The IDBM procedure exhibits the attractive property of realizing a valid coupling between the target measures at each step. We perform an initial theoretical investigation of the IDBM procedure, establishing its convergence properties. The theoretical findings are complemented by numerous numerical experiments illustrating the competitive performance of the IDBM procedure across various applications. Recent advancements in generative modeling employ the time-reversal of a diffusion process to define a generative process that approximately transports a simple distribution to the data distribution. As an alternative, we propose using the first iteration of the IDBM procedure as an approximation-free method for realizing this transport. This approach offers greater flexibility in selecting the generative process dynamics and exhibits faster training and superior sample quality over longer discretization intervals. In terms of implementation, the necessary modifications are minimally intrusive, being limited to the training loss computation, with no changes necessary for generative sampling.

Neural tangent kernel analysis of shallow $α$-Stable ReLU neural networks

There is a recent literature on large-width properties of Gaussian neural networks (NNs), i.e. NNs whose weights are distributed according to Gaussian distributions. Two popular problems are: i) the study of the large-width behaviour of NNs, which provided a characterization of the infinitely wide limit of a rescaled NN in terms of a Gaussian process; ii) the study of the training dynamics of NNs, which set forth a large-width equivalence between training the rescaled NN and performing a kernel regression with a deterministic kernel referred to as the neural tangent kernel (NTK). In this paper, we consider these problems for $\alpha$-Stable NNs, which generalize Gaussian NNs by assuming that the NN's weights are distributed as $\alpha$-Stable distributions with $\alpha\in(0,2]$, i.e. distributions with heavy tails. For shallow $\alpha$-Stable NNs with a ReLU activation function, we show that if the NN's width goes to infinity then a rescaled NN converges weakly to an $\alpha$-Stable process, i.e. a stochastic process with $\alpha$-Stable finite-dimensional distributions. As a novelty with respect to the Gaussian setting, in the $\alpha$-Stable setting the choice of the activation function affects the scaling of the NN, namely: to achieve the infinitely wide $\alpha$-Stable process, the ReLU function requires an additional logarithmic scaling with respect to sub-linear functions. Then, our main contribution is the NTK analysis of shallow $\alpha$-Stable ReLU-NNs, which leads to a large-width equivalence between training a rescaled NN and performing a kernel regression with an $(\alpha/2)$-Stable random kernel. The randomness of such a kernel is a novelty with respect to the Gaussian setting, namely: in the $\alpha$-Stable setting the randomness of the NN at initialization does not vanish in the NTK analysis, thus inducing a distribution for the kernel of the underlying kernel regression.

Deep Stable neural networks: large-width asymptotics and convergence rates

In modern deep learning, there is a recent and growing literature on the interplay between large-width asymptotics for deep Gaussian neural networks (NNs), i.e. deep NNs with Gaussian-distributed weights, and classes of Gaussian stochastic processes (SPs). Such an interplay has proved to be critical in several contexts of practical interest, e.g. Bayesian inference under Gaussian SP priors, kernel regression for infinite-wide deep NNs trained via gradient descent, and information propagation within infinite-wide NNs. Motivated by empirical analysis, showing the potential of replacing Gaussian distributions with Stable distributions for the NN's weights, in this paper we investigate large-width asymptotics for (fully connected) feed-forward deep Stable NNs, i.e. deep NNs with Stable-distributed weights. First, we show that as the width goes to infinity jointly over the NN's layers, a suitable rescaled deep Stable NN converges weakly to a Stable SP whose distribution is characterized recursively through the NN's layers. Because of the non-triangular NN's structure, this is a non-standard asymptotic problem, to which we propose a novel and self-contained inductive approach, which may be of independent interest. Then, we establish sup-norm convergence rates of a deep Stable NN to a Stable SP, quantifying the critical difference between the settings of ``joint growth" and ``sequential growth" of the width over the NN's layers. Our work extends recent results on infinite-wide limits for deep Gaussian NNs to the more general deep Stable NNs, providing the first result on convergence rates for infinite-wide deep NNs.

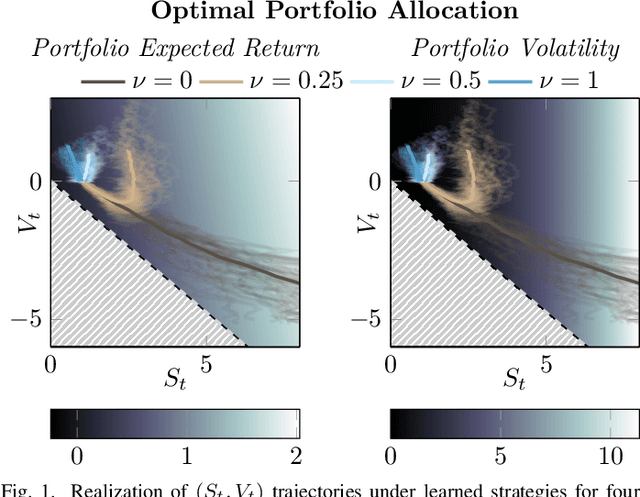
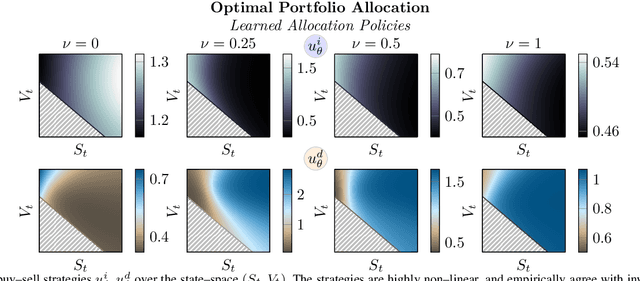
Learning Stochastic Optimal Policies via Gradient Descent

We systematically develop a learning-based treatment of stochastic optimal control (SOC), relying on direct optimization of parametric control policies. We propose a derivation of adjoint sensitivity results for stochastic differential equations through direct application of variational calculus. Then, given an objective function for a predetermined task specifying the desiderata for the controller, we optimize their parameters via iterative gradient descent methods. In doing so, we extend the range of applicability of classical SOC techniques, often requiring strict assumptions on the functional form of system and control. We verify the performance of the proposed approach on a continuous-time, finite horizon portfolio optimization with proportional transaction costs.

Large-width functional asymptotics for deep Gaussian neural networks

In this paper, we consider fully connected feed-forward deep neural networks where weights and biases are independent and identically distributed according to Gaussian distributions. Extending previous results (Matthews et al., 2018a;b; Yang, 2019) we adopt a function-space perspective, i.e. we look at neural networks as infinite-dimensional random elements on the input space $\mathbb{R}^I$. Under suitable assumptions on the activation function we show that: i) a network defines a continuous Gaussian process on the input space $\mathbb{R}^I$; ii) a network with re-scaled weights converges weakly to a continuous Gaussian process in the large-width limit; iii) the limiting Gaussian process has almost surely locally $\gamma$-H\"older continuous paths, for $0 < \gamma <1$. Our results contribute to recent theoretical studies on the interplay between infinitely wide deep neural networks and Gaussian processes by establishing weak convergence in function-space with respect to a stronger metric.

A Bayesian nonparametric approach to count-min sketch under power-law data streams

The count-min sketch (CMS) is a randomized data structure that provides estimates of tokens' frequencies in a large data stream using a compressed representation of the data by random hashing. In this paper, we rely on a recent Bayesian nonparametric (BNP) view on the CMS to develop a novel learning-augmented CMS under power-law data streams. We assume that tokens in the stream are drawn from an unknown discrete distribution, which is endowed with a normalized inverse Gaussian process (NIGP) prior. Then, using distributional properties of the NIGP, we compute the posterior distribution of a token's frequency in the stream, given the hashed data, and in turn corresponding BNP estimates. Applications to synthetic and real data show that our approach achieves a remarkable performance in the estimation of low-frequency tokens. This is known to be a desirable feature in the context of natural language processing, where it is indeed common in the context of the power-law behaviour of the data.

Learning-augmented count-min sketches via Bayesian nonparametrics

The count-min sketch (CMS) is a time and memory efficient randomized data structure that provides estimates of tokens' frequencies in a data stream, i.e. point queries, based on random hashed data. Learning-augmented CMSs improve the CMS by learning models that allow to better exploit data properties. In this paper, we focus on the learning-augmented CMS of Cai, Mitzenmacher and Adams (\textit{NeurIPS} 2018), which relies on Bayesian nonparametric (BNP) modeling of a data stream via Dirichlet process (DP) priors. This is referred to as the CMS-DP, and it leads to BNP estimates of a point query as posterior means of the point query given the hashed data. While BNPs is proved to be a powerful tool for developing robust learning-augmented CMSs, ideas and methods behind the CMS-DP are tailored to point queries under DP priors, and they can not be used for other priors or more general queries. In this paper, we present an alternative, and more flexible, derivation of the CMS-DP such that: i) it allows to make use of the Pitman-Yor process (PYP) prior, which is arguably the most popular generalization of the DP prior; ii) it can be readily applied to the more general problem of estimating range queries. This leads to develop a novel learning-augmented CMS under power-law data streams, referred to as the CMS-PYP, which relies on BNP modeling of the stream via PYP priors. Applications to synthetic and real data show that the CMS-PYP outperforms the CMS and the CMS-DP in the estimation of low-frequency tokens; this known to be a critical feature in natural language processing, where it is indeed common to encounter power-law data streams.

Infinite-channel deep stable convolutional neural networks

The interplay between infinite-width neural networks (NNs) and classes of Gaussian processes (GPs) is well known since the seminal work of Neal (1996). While numerous theoretical refinements have been proposed in the recent years, the interplay between NNs and GPs relies on two critical distributional assumptions on the NN's parameters: A1) finite variance; A2) independent and identical distribution (iid). In this paper, we consider the problem of removing A1 in the general context of deep feed-forward convolutional NNs. In particular, we assume iid parameters distributed according to a stable distribution and we show that the infinite-channel limit of a deep feed-forward convolutional NNs, under suitable scaling, is a stochastic process with multivariate stable finite-dimensional distributions. Such a limiting distribution is then characterized through an explicit backward recursion for its parameters over the layers. Our contribution extends results of Favaro et al. (2020) to convolutional architectures, and it paves the way to expand exciting recent lines of research that rely on classes of GP limits.