Improved prediction of future user activity in online A/B testing
Paper and Code
Feb 05, 2024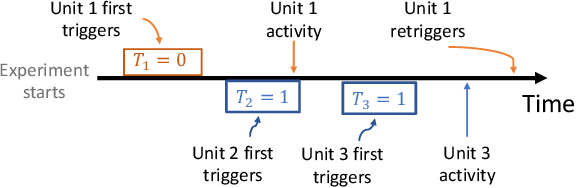

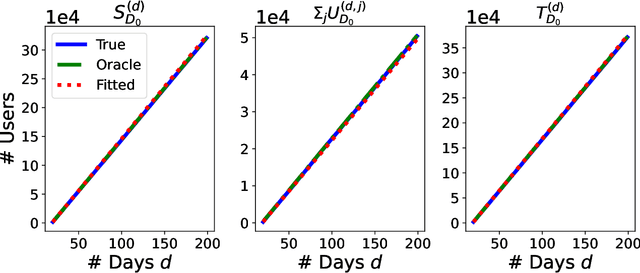
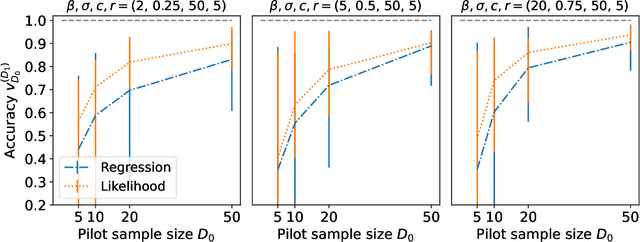
In online randomized experiments or A/B tests, accurate predictions of participant inclusion rates are of paramount importance. These predictions not only guide experimenters in optimizing the experiment's duration but also enhance the precision of treatment effect estimates. In this paper we present a novel, straightforward, and scalable Bayesian nonparametric approach for predicting the rate at which individuals will be exposed to interventions within the realm of online A/B testing. Our approach stands out by offering dual prediction capabilities: it forecasts both the quantity of new customers expected in future time windows and, unlike available alternative methods, the number of times they will be observed. We derive closed-form expressions for the posterior distributions of the quantities needed to form predictions about future user activity, thereby bypassing the need for numerical algorithms such as Markov chain Monte Carlo. After a comprehensive exposition of our model, we test its performance on experiments on real and simulated data, where we show its superior performance with respect to existing alternatives in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge