Improved prediction of future user activity in online A/B testing

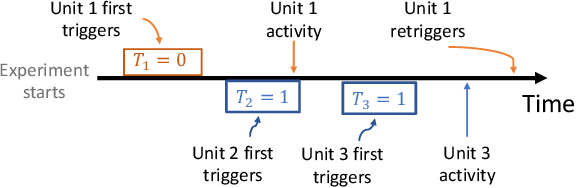
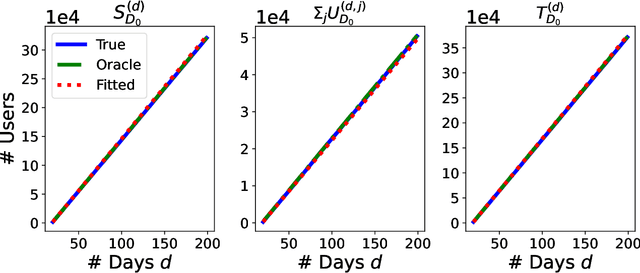
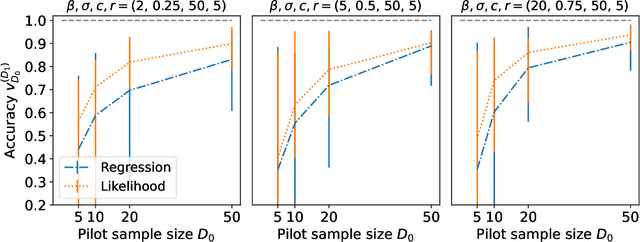
In online randomized experiments or A/B tests, accurate predictions of participant inclusion rates are of paramount importance. These predictions not only guide experimenters in optimizing the experiment's duration but also enhance the precision of treatment effect estimates. In this paper we present a novel, straightforward, and scalable Bayesian nonparametric approach for predicting the rate at which individuals will be exposed to interventions within the realm of online A/B testing. Our approach stands out by offering dual prediction capabilities: it forecasts both the quantity of new customers expected in future time windows and, unlike available alternative methods, the number of times they will be observed. We derive closed-form expressions for the posterior distributions of the quantities needed to form predictions about future user activity, thereby bypassing the need for numerical algorithms such as Markov chain Monte Carlo. After a comprehensive exposition of our model, we test its performance on experiments on real and simulated data, where we show its superior performance with respect to existing alternatives in the literature.

A Nonparametric Bayes Approach to Online Activity Prediction

Accurately predicting the onset of specific activities within defined timeframes holds significant importance in several applied contexts. In particular, accurate prediction of the number of future users that will be exposed to an intervention is an important piece of information for experimenters running online experiments (A/B tests). In this work, we propose a novel approach to predict the number of users that will be active in a given time period, as well as the temporal trajectory needed to attain a desired user participation threshold. We model user activity using a Bayesian nonparametric approach which allows us to capture the underlying heterogeneity in user engagement. We derive closed-form expressions for the number of new users expected in a given period, and a simple Monte Carlo algorithm targeting the posterior distribution of the number of days needed to attain a desired number of users; the latter is important for experimental planning. We illustrate the performance of our approach via several experiments on synthetic and real world data, in which we show that our novel method outperforms existing competitors.

Frequency and cardinality recovery from sketched data: a novel approach bridging Bayesian and frequentist views

We study how to recover the frequency of a symbol in a large discrete data set, using only a compressed representation, or sketch, of those data obtained via random hashing. This is a classical problem in computer science, with various algorithms available, such as the count-min sketch. However, these algorithms often assume that the data are fixed, leading to overly conservative and potentially inaccurate estimates when dealing with randomly sampled data. In this paper, we consider the sketched data as a random sample from an unknown distribution, and then we introduce novel estimators that improve upon existing approaches. Our method combines Bayesian nonparametric and classical (frequentist) perspectives, addressing their unique limitations to provide a principled and practical solution. Additionally, we extend our method to address the related but distinct problem of cardinality recovery, which consists of estimating the total number of distinct objects in the data set. We validate our method on synthetic and real data, comparing its performance to state-of-the-art alternatives.

Projected Statistical Methods for Distributional Data on the Real Line with the Wasserstein Metric

We present a novel class of projected methods, to perform statistical analysis on a data set of probability distributions on the real line, with the 2-Wasserstein metric. We focus in particular on Principal Component Analysis (PCA) and regression. To define these models, we exploit a representation of the Wasserstein space closely related to its weak Riemannian structure, by mapping the data to a suitable linear space and using a metric projection operator to constrain the results in the Wasserstein space. By carefully choosing the tangent point, we are able to derive fast empirical methods, exploiting a constrained B-spline approximation. As a byproduct of our approach, we are also able to derive faster routines for previous work on PCA for distributions. By means of simulation studies, we compare our approaches to previously proposed methods, showing that our projected PCA has similar performance for a fraction of the computational cost and that the projected regression is extremely flexible even under misspecification. Several theoretical properties of the models are investigated and asymptotic consistency is proven. Two real world applications to Covid-19 mortality in the US and wind speed forecasting are discussed.

Feature Selection via Mutual Information: New Theoretical Insights

Mutual information has been successfully adopted in filter feature-selection methods to assess both the relevancy of a subset of features in predicting the target variable and the redundancy with respect to other variables. However, existing algorithms are mostly heuristic and do not offer any guarantee on the proposed solution. In this paper, we provide novel theoretical results showing that conditional mutual information naturally arises when bounding the ideal regression/classification errors achieved by different subsets of features. Leveraging on these insights, we propose a novel stopping condition for backward and forward greedy methods which ensures that the ideal prediction error using the selected feature subset remains bounded by a user-specified threshold. We provide numerical simulations to support our theoretical claims and compare to common heuristic methods.