Imaging-based representation and stratification of intra-tumor Heterogeneity via tree-edit distance

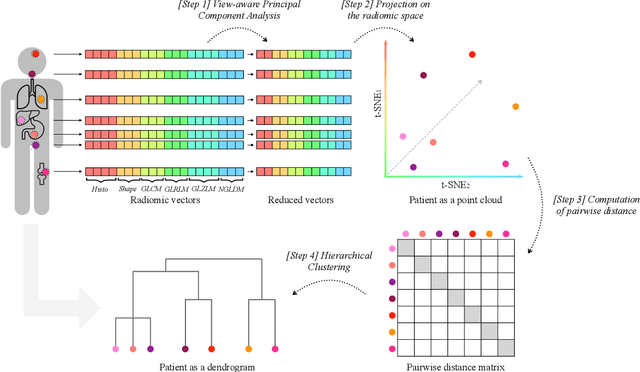
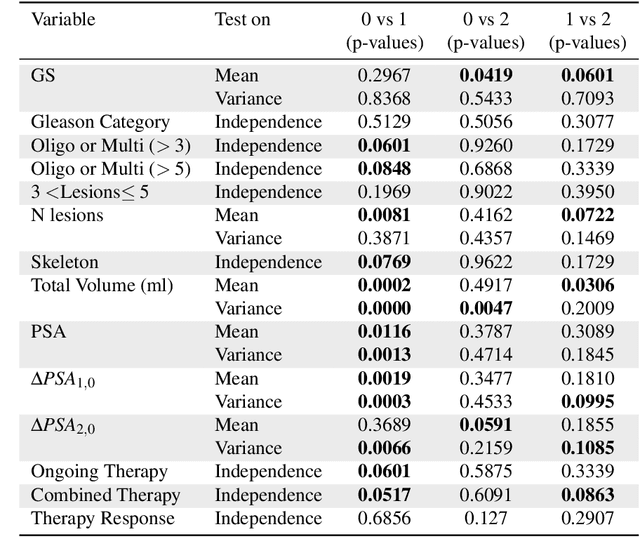
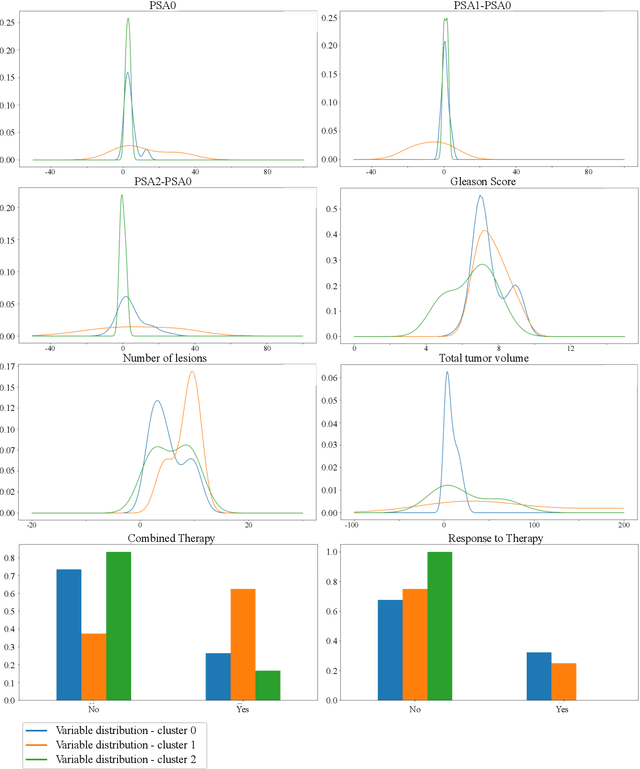
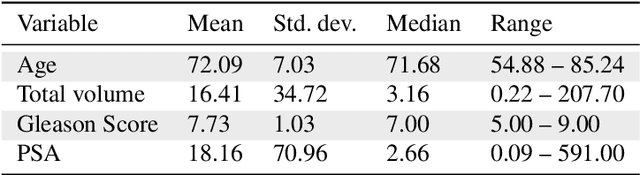
Personalized medicine is the future of medical practice. In oncology, tumor heterogeneity assessment represents a pivotal step for effective treatment planning and prognosis prediction. Despite new procedures for DNA sequencing and analysis, non-invasive methods for tumor characterization are needed to impact on daily routine. On purpose, imaging texture analysis is rapidly scaling, holding the promise to surrogate histopathological assessment of tumor lesions. In this work, we propose a tree-based representation strategy for describing intra-tumor heterogeneity of patients affected by metastatic cancer. We leverage radiomics information extracted from PET/CT imaging and we provide an exhaustive and easily readable summary of the disease spreading. We exploit this novel patient representation to perform cancer subtyping according to hierarchical clustering technique. To this purpose, a new heterogeneity-based distance between trees is defined and applied to a case study of Prostate Cancer (PCa). Clusters interpretation is explored in terms of concordance with severity status, tumor burden and biological characteristics. Results are promising, as the proposed method outperforms current literature approaches. Ultimately, the proposed methods draws a general analysis framework that would allow to extract knowledge from daily acquired imaging data of patients and provide insights for effective treatment planning.

Projected Statistical Methods for Distributional Data on the Real Line with the Wasserstein Metric

We present a novel class of projected methods, to perform statistical analysis on a data set of probability distributions on the real line, with the 2-Wasserstein metric. We focus in particular on Principal Component Analysis (PCA) and regression. To define these models, we exploit a representation of the Wasserstein space closely related to its weak Riemannian structure, by mapping the data to a suitable linear space and using a metric projection operator to constrain the results in the Wasserstein space. By carefully choosing the tangent point, we are able to derive fast empirical methods, exploiting a constrained B-spline approximation. As a byproduct of our approach, we are also able to derive faster routines for previous work on PCA for distributions. By means of simulation studies, we compare our approaches to previously proposed methods, showing that our projected PCA has similar performance for a fraction of the computational cost and that the projected regression is extremely flexible even under misspecification. Several theoretical properties of the models are investigated and asymptotic consistency is proven. Two real world applications to Covid-19 mortality in the US and wind speed forecasting are discussed.