Zero-Shot Whole-Body Humanoid Control via Behavioral Foundation Models

Unsupervised reinforcement learning (RL) aims at pre-training agents that can solve a wide range of downstream tasks in complex environments. Despite recent advancements, existing approaches suffer from several limitations: they may require running an RL process on each downstream task to achieve a satisfactory performance, they may need access to datasets with good coverage or well-curated task-specific samples, or they may pre-train policies with unsupervised losses that are poorly correlated with the downstream tasks of interest. In this paper, we introduce a novel algorithm regularizing unsupervised RL towards imitating trajectories from unlabeled behavior datasets. The key technical novelty of our method, called Forward-Backward Representations with Conditional-Policy Regularization, is to train forward-backward representations to embed the unlabeled trajectories to the same latent space used to represent states, rewards, and policies, and use a latent-conditional discriminator to encourage policies to ``cover'' the states in the unlabeled behavior dataset. As a result, we can learn policies that are well aligned with the behaviors in the dataset, while retaining zero-shot generalization capabilities for reward-based and imitation tasks. We demonstrate the effectiveness of this new approach in a challenging humanoid control problem: leveraging observation-only motion capture datasets, we train Meta Motivo, the first humanoid behavioral foundation model that can be prompted to solve a variety of whole-body tasks, including motion tracking, goal reaching, and reward optimization. The resulting model is capable of expressing human-like behaviors and it achieves competitive performance with task-specific methods while outperforming state-of-the-art unsupervised RL and model-based baselines.

Fast Adaptation with Behavioral Foundation Models

Unsupervised zero-shot reinforcement learning (RL) has emerged as a powerful paradigm for pretraining behavioral foundation models (BFMs), enabling agents to solve a wide range of downstream tasks specified via reward functions in a zero-shot fashion, i.e., without additional test-time learning or planning. This is achieved by learning self-supervised task embeddings alongside corresponding near-optimal behaviors and incorporating an inference procedure to directly retrieve the latent task embedding and associated policy for any given reward function. Despite promising results, zero-shot policies are often suboptimal due to errors induced by the unsupervised training process, the embedding, and the inference procedure. In this paper, we focus on devising fast adaptation strategies to improve the zero-shot performance of BFMs in a few steps of online interaction with the environment while avoiding any performance drop during the adaptation process. Notably, we demonstrate that existing BFMs learn a set of skills containing more performant policies than those identified by their inference procedure, making them well-suited for fast adaptation. Motivated by this observation, we propose both actor-critic and actor-only fast adaptation strategies that search in the low-dimensional task-embedding space of the pre-trained BFM to rapidly improve the performance of its zero-shot policies on any downstream task. Notably, our approach mitigates the initial "unlearning" phase commonly observed when fine-tuning pre-trained RL models. We evaluate our fast adaptation strategies on top of four state-of-the-art zero-shot RL methods in multiple navigation and locomotion domains. Our results show that they achieve 10-40% improvement over their zero-shot performance in a few tens of episodes, outperforming existing baselines.

Temporal Difference Flows

Predictive models of the future are fundamental for an agent's ability to reason and plan. A common strategy learns a world model and unrolls it step-by-step at inference, where small errors can rapidly compound. Geometric Horizon Models (GHMs) offer a compelling alternative by directly making predictions of future states, avoiding cumulative inference errors. While GHMs can be conveniently learned by a generative analog to temporal difference (TD) learning, existing methods are negatively affected by bootstrapping predictions at train time and struggle to generate high-quality predictions at long horizons. This paper introduces Temporal Difference Flows (TD-Flow), which leverages the structure of a novel Bellman equation on probability paths alongside flow-matching techniques to learn accurate GHMs at over 5x the horizon length of prior methods. Theoretically, we establish a new convergence result and primarily attribute TD-Flow's efficacy to reduced gradient variance during training. We further show that similar arguments can be extended to diffusion-based methods. Empirically, we validate TD-Flow across a diverse set of domains on both generative metrics and downstream tasks including policy evaluation. Moreover, integrating TD-Flow with recent behavior foundation models for planning over pre-trained policies demonstrates substantial performance gains, underscoring its promise for long-horizon decision-making.

Simple Ingredients for Offline Reinforcement Learning

Offline reinforcement learning algorithms have proven effective on datasets highly connected to the target downstream task. Yet, leveraging a novel testbed (MOOD) in which trajectories come from heterogeneous sources, we show that existing methods struggle with diverse data: their performance considerably deteriorates as data collected for related but different tasks is simply added to the offline buffer. In light of this finding, we conduct a large empirical study where we formulate and test several hypotheses to explain this failure. Surprisingly, we find that scale, more than algorithmic considerations, is the key factor influencing performance. We show that simple methods like AWAC and IQL with increased network size overcome the paradoxical failure modes from the inclusion of additional data in MOOD, and notably outperform prior state-of-the-art algorithms on the canonical D4RL benchmark.

Towards Instance-Optimality in Online PAC Reinforcement Learning

Several recent works have proposed instance-dependent upper bounds on the number of episodes needed to identify, with probability $1-\delta$, an $\varepsilon$-optimal policy in finite-horizon tabular Markov Decision Processes (MDPs). These upper bounds feature various complexity measures for the MDP, which are defined based on different notions of sub-optimality gaps. However, as of now, no lower bound has been established to assess the optimality of any of these complexity measures, except for the special case of MDPs with deterministic transitions. In this paper, we propose the first instance-dependent lower bound on the sample complexity required for the PAC identification of a near-optimal policy in any tabular episodic MDP. Additionally, we demonstrate that the sample complexity of the PEDEL algorithm of \cite{Wagenmaker22linearMDP} closely approaches this lower bound. Considering the intractability of PEDEL, we formulate an open question regarding the possibility of achieving our lower bound using a computationally-efficient algorithm.

Active Coverage for PAC Reinforcement Learning

Collecting and leveraging data with good coverage properties plays a crucial role in different aspects of reinforcement learning (RL), including reward-free exploration and offline learning. However, the notion of "good coverage" really depends on the application at hand, as data suitable for one context may not be so for another. In this paper, we formalize the problem of active coverage in episodic Markov decision processes (MDPs), where the goal is to interact with the environment so as to fulfill given sampling requirements. This framework is sufficiently flexible to specify any desired coverage property, making it applicable to any problem that involves online exploration. Our main contribution is an instance-dependent lower bound on the sample complexity of active coverage and a simple game-theoretic algorithm, CovGame, that nearly matches it. We then show that CovGame can be used as a building block to solve different PAC RL tasks. In particular, we obtain a simple algorithm for PAC reward-free exploration with an instance-dependent sample complexity that, in certain MDPs which are "easy to explore", is lower than the minimax one. By further coupling this exploration algorithm with a new technique to do implicit eliminations in policy space, we obtain a computationally-efficient algorithm for best-policy identification whose instance-dependent sample complexity scales with gaps between policy values.

Layered State Discovery for Incremental Autonomous Exploration

We study the autonomous exploration (AX) problem proposed by Lim & Auer (2012). In this setting, the objective is to discover a set of $\epsilon$-optimal policies reaching a set $\mathcal{S}_L^{\rightarrow}$ of incrementally $L$-controllable states. We introduce a novel layered decomposition of the set of incrementally $L$-controllable states that is based on the iterative application of a state-expansion operator. We leverage these results to design Layered Autonomous Exploration (LAE), a novel algorithm for AX that attains a sample complexity of $\tilde{\mathcal{O}}(LS^{\rightarrow}_{L(1+\epsilon)}\Gamma_{L(1+\epsilon)} A \ln^{12}(S^{\rightarrow}_{L(1+\epsilon)})/\epsilon^2)$, where $S^{\rightarrow}_{L(1+\epsilon)}$ is the number of states that are incrementally $L(1+\epsilon)$-controllable, $A$ is the number of actions, and $\Gamma_{L(1+\epsilon)}$ is the branching factor of the transitions over such states. LAE improves over the algorithm of Tarbouriech et al. (2020a) by a factor of $L^2$ and it is the first algorithm for AX that works in a countably-infinite state space. Moreover, we show that, under a certain identifiability assumption, LAE achieves minimax-optimal sample complexity of $\tilde{\mathcal{O}}(LS^{\rightarrow}_{L}A\ln^{12}(S^{\rightarrow}_{L})/\epsilon^2)$, outperforming existing algorithms and matching for the first time the lower bound proved by Cai et al. (2022) up to logarithmic factors.

On the Complexity of Representation Learning in Contextual Linear Bandits

In contextual linear bandits, the reward function is assumed to be a linear combination of an unknown reward vector and a given embedding of context-arm pairs. In practice, the embedding is often learned at the same time as the reward vector, thus leading to an online representation learning problem. Existing approaches to representation learning in contextual bandits are either very generic (e.g., model-selection techniques or algorithms for learning with arbitrary function classes) or specialized to particular structures (e.g., nested features or representations with certain spectral properties). As a result, the understanding of the cost of representation learning in contextual linear bandit is still limited. In this paper, we take a systematic approach to the problem and provide a comprehensive study through an instance-dependent perspective. We show that representation learning is fundamentally more complex than linear bandits (i.e., learning with a given representation). In particular, learning with a given set of representations is never simpler than learning with the worst realizable representation in the set, while we show cases where it can be arbitrarily harder. We complement this result with an extensive discussion of how it relates to existing literature and we illustrate positive instances where representation learning is as complex as learning with a fixed representation and where sub-logarithmic regret is achievable.

Scalable Representation Learning in Linear Contextual Bandits with Constant Regret Guarantees

We study the problem of representation learning in stochastic contextual linear bandits. While the primary concern in this domain is usually to find realizable representations (i.e., those that allow predicting the reward function at any context-action pair exactly), it has been recently shown that representations with certain spectral properties (called HLS) may be more effective for the exploration-exploitation task, enabling LinUCB to achieve constant (i.e., horizon-independent) regret. In this paper, we propose BanditSRL, a representation learning algorithm that combines a novel constrained optimization problem to learn a realizable representation with good spectral properties with a generalized likelihood ratio test to exploit the recovered representation and avoid excessive exploration. We prove that BanditSRL can be paired with any no-regret algorithm and achieve constant regret whenever an HLS representation is available. Furthermore, BanditSRL can be easily combined with deep neural networks and we show how regularizing towards HLS representations is beneficial in standard benchmarks.

Reaching Goals is Hard: Settling the Sample Complexity of the Stochastic Shortest Path

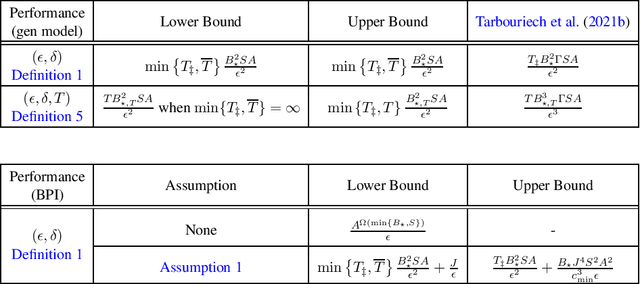
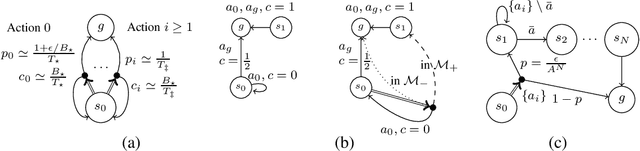
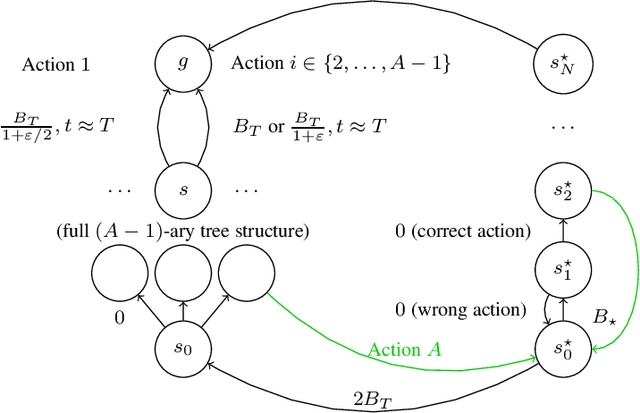
We study the sample complexity of learning an $\epsilon$-optimal policy in the Stochastic Shortest Path (SSP) problem. We first derive sample complexity bounds when the learner has access to a generative model. We show that there exists a worst-case SSP instance with $S$ states, $A$ actions, minimum cost $c_{\min}$, and maximum expected cost of the optimal policy over all states $B_{\star}$, where any algorithm requires at least $\Omega(SAB_{\star}^3/(c_{\min}\epsilon^2))$ samples to return an $\epsilon$-optimal policy with high probability. Surprisingly, this implies that whenever $c_{\min}=0$ an SSP problem may not be learnable, thus revealing that learning in SSPs is strictly harder than in the finite-horizon and discounted settings. We complement this result with lower bounds when prior knowledge of the hitting time of the optimal policy is available and when we restrict optimality by competing against policies with bounded hitting time. Finally, we design an algorithm with matching upper bounds in these cases. This settles the sample complexity of learning $\epsilon$-optimal polices in SSP with generative models. We also initiate the study of learning $\epsilon$-optimal policies without access to a generative model (i.e., the so-called best-policy identification problem), and show that sample-efficient learning is impossible in general. On the other hand, efficient learning can be made possible if we assume the agent can directly reach the goal state from any state by paying a fixed cost. We then establish the first upper and lower bounds under this assumption. Finally, using similar analytic tools, we prove that horizon-free regret is impossible in SSPs under general costs, resolving an open problem in (Tarbouriech et al., 2021c).