Teaching Language Models to Critique via Reinforcement Learning

Teaching large language models (LLMs) to critique and refine their outputs is crucial for building systems that can iteratively improve, yet it is fundamentally limited by the ability to provide accurate judgments and actionable suggestions. In this work, we study LLM critics for code generation and propose $\texttt{CTRL}$, a framework for $\texttt{C}$ritic $\texttt{T}$raining via $\texttt{R}$einforcement $\texttt{L}$earning, which trains a critic model to generate feedback that maximizes correction performance for a fixed generator model without human supervision. Our results demonstrate that critics trained with $\texttt{CTRL}$ significantly enhance pass rates and mitigate compounding errors across both base and stronger generator models. Furthermore, we show that these critic models act as accurate generative reward models and enable test-time scaling through iterative critique-revision, achieving up to 106.1% relative improvements across challenging code generation benchmarks.

TACLR: A Scalable and Efficient Retrieval-based Method for Industrial Product Attribute Value Identification

Product Attribute Value Identification (PAVI) involves identifying attribute values from product profiles, a key task for improving product search, recommendations, and business analytics on e-commerce platforms. However, existing PAVI methods face critical challenges, such as inferring implicit values, handling out-of-distribution (OOD) values, and producing normalized outputs. To address these limitations, we introduce Taxonomy-Aware Contrastive Learning Retrieval (TACLR), the first retrieval-based method for PAVI. TACLR formulates PAVI as an information retrieval task by encoding product profiles and candidate values into embeddings and retrieving values based on their similarity to the item embedding. It leverages contrastive training with taxonomy-aware hard negative sampling and employs adaptive inference with dynamic thresholds. TACLR offers three key advantages: (1) it effectively handles implicit and OOD values while producing normalized outputs; (2) it scales to thousands of categories, tens of thousands of attributes, and millions of values; and (3) it supports efficient inference for high-load industrial scenarios. Extensive experiments on proprietary and public datasets validate the effectiveness and efficiency of TACLR. Moreover, it has been successfully deployed in a real-world e-commerce platform, processing millions of product listings daily while supporting dynamic, large-scale attribute taxonomies.

Reward-Augmented Data Enhances Direct Preference Alignment of LLMs

Preference alignment in Large Language Models (LLMs) has significantly improved their ability to adhere to human instructions and intentions. However, existing direct alignment algorithms primarily focus on relative preferences and often overlook the qualitative aspects of responses. Striving to maximize the implicit reward gap between the chosen and the slightly inferior rejected responses can cause overfitting and unnecessary unlearning of the high-quality rejected responses. The unawareness of the reward scores also drives the LLM to indiscriminately favor the low-quality chosen responses and fail to generalize to responses with the highest rewards, which are sparse in data. To overcome these shortcomings, our study introduces reward-conditioned LLM policies that discern and learn from the entire spectrum of response quality within the dataset, helping extrapolate to more optimal regions. We propose an effective yet simple data relabeling method that conditions the preference pairs on quality scores to construct a reward-augmented dataset. This dataset is easily integrated with existing direct alignment algorithms and is applicable to any preference dataset. The experimental results across instruction-following benchmarks including AlpacaEval, MT-Bench, and Arena-Hard-Auto demonstrate that our approach consistently boosts the performance of DPO by a considerable margin across diverse models. Additionally, our method improves the average accuracy on various academic benchmarks. When applying our method to on-policy data, the resulting DPO model achieves SOTA results on AlpacaEval. Through ablation studies, we demonstrate that our method not only maximizes the utility of preference data but also mitigates the issue of unlearning, demonstrating its broad effectiveness beyond mere dataset expansion. Our code is available at https://github.com/shenao-zhang/reward-augmented-preference.

BabelBench: An Omni Benchmark for Code-Driven Analysis of Multimodal and Multistructured Data

Large language models (LLMs) have become increasingly pivotal across various domains, especially in handling complex data types. This includes structured data processing, as exemplified by ChartQA and ChatGPT-Ada, and multimodal unstructured data processing as seen in Visual Question Answering (VQA). These areas have attracted significant attention from both industry and academia. Despite this, there remains a lack of unified evaluation methodologies for these diverse data handling scenarios. In response, we introduce BabelBench, an innovative benchmark framework that evaluates the proficiency of LLMs in managing multimodal multistructured data with code execution. BabelBench incorporates a dataset comprising 247 meticulously curated problems that challenge the models with tasks in perception, commonsense reasoning, logical reasoning, and so on. Besides the basic capabilities of multimodal understanding, structured data processing as well as code generation, these tasks demand advanced capabilities in exploration, planning, reasoning and debugging. Our experimental findings on BabelBench indicate that even cutting-edge models like ChatGPT 4 exhibit substantial room for improvement. The insights derived from our comprehensive analysis offer valuable guidance for future research within the community. The benchmark data can be found at https://github.com/FFD8FFE/babelbench.

Effective Diffusion Transformer Architecture for Image Super-Resolution

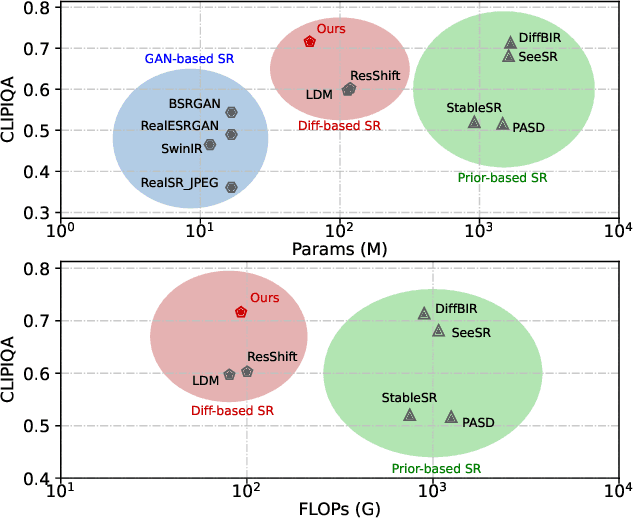
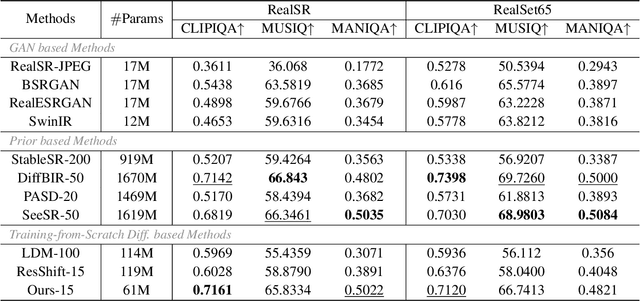
Recent advances indicate that diffusion models hold great promise in image super-resolution. While the latest methods are primarily based on latent diffusion models with convolutional neural networks, there are few attempts to explore transformers, which have demonstrated remarkable performance in image generation. In this work, we design an effective diffusion transformer for image super-resolution (DiT-SR) that achieves the visual quality of prior-based methods, but through a training-from-scratch manner. In practice, DiT-SR leverages an overall U-shaped architecture, and adopts a uniform isotropic design for all the transformer blocks across different stages. The former facilitates multi-scale hierarchical feature extraction, while the latter reallocates the computational resources to critical layers to further enhance performance. Moreover, we thoroughly analyze the limitation of the widely used AdaLN, and present a frequency-adaptive time-step conditioning module, enhancing the model's capacity to process distinct frequency information at different time steps. Extensive experiments demonstrate that DiT-SR outperforms the existing training-from-scratch diffusion-based SR methods significantly, and even beats some of the prior-based methods on pretrained Stable Diffusion, proving the superiority of diffusion transformer in image super-resolution.

Collaboration of Teachers for Semi-supervised Object Detection

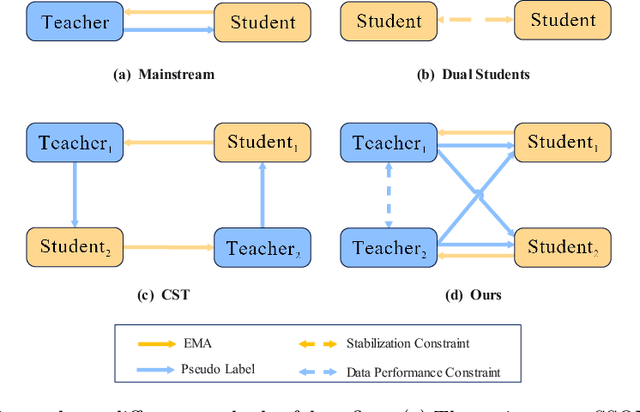
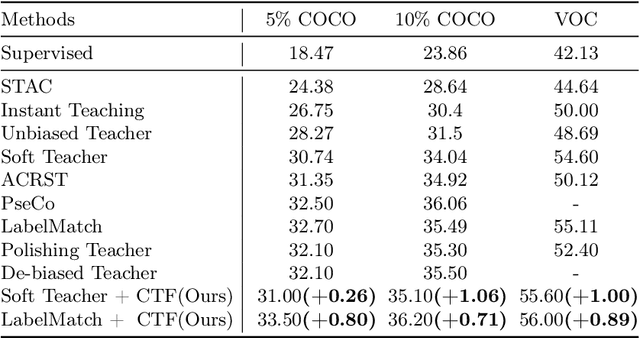
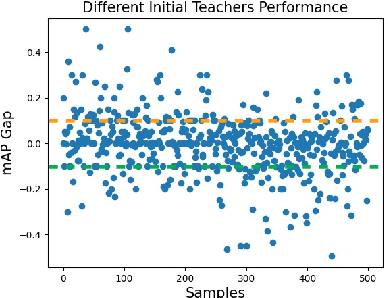
Recent semi-supervised object detection (SSOD) has achieved remarkable progress by leveraging unlabeled data for training. Mainstream SSOD methods rely on Consistency Regularization methods and Exponential Moving Average (EMA), which form a cyclic data flow. However, the EMA updating training approach leads to weight coupling between the teacher and student models. This coupling in a cyclic data flow results in a decrease in the utilization of unlabeled data information and the confirmation bias on low-quality or erroneous pseudo-labels. To address these issues, we propose the Collaboration of Teachers Framework (CTF), which consists of multiple pairs of teacher and student models for training. In the learning process of CTF, the Data Performance Consistency Optimization module (DPCO) informs the best pair of teacher models possessing the optimal pseudo-labels during the past training process, and these most reliable pseudo-labels generated by the best performing teacher would guide the other student models. As a consequence, this framework greatly improves the utilization of unlabeled data and prevents the positive feedback cycle of unreliable pseudo-labels. The CTF achieves outstanding results on numerous SSOD datasets, including a 0.71% mAP improvement on the 10% annotated COCO dataset and a 0.89% mAP improvement on the VOC dataset compared to LabelMatch and converges significantly faster. Moreover, the CTF is plug-and-play and can be integrated with other mainstream SSOD methods.

$\mathbf{}$-Puzzle: A Cost-Efficient Testbed for Benchmarking Reinforcement Learning Algorithms in Generative Language Model

Recent advances in reinforcement learning (RL) algorithms aim to enhance the performance of language models at scale. Yet, there is a noticeable absence of a cost-effective and standardized testbed tailored to evaluating and comparing these algorithms. To bridge this gap, we present a generalized version of the 24-Puzzle: the $(N,K)$-Puzzle, which challenges language models to reach a target value $K$ with $N$ integers. We evaluate the effectiveness of established RL algorithms such as Proximal Policy Optimization (PPO), alongside novel approaches like Identity Policy Optimization (IPO) and Direct Policy Optimization (DPO).

$\mathcal{B}$-Coder: Value-Based Deep Reinforcement Learning for Program Synthesis

Program synthesis aims to create accurate, executable code from natural language descriptions. This field has leveraged the power of reinforcement learning (RL) in conjunction with large language models (LLMs), significantly enhancing code generation capabilities. This integration focuses on directly optimizing functional correctness, transcending conventional supervised losses. While current literature predominantly favors policy-based algorithms, attributes of program synthesis suggest a natural compatibility with value-based methods. This stems from rich collection of off-policy programs developed by human programmers, and the straightforward verification of generated programs through automated unit testing (i.e. easily obtainable rewards in RL language). Diverging from the predominant use of policy-based algorithms, our work explores the applicability of value-based approaches, leading to the development of our $\mathcal{B}$-Coder (pronounced Bellman coder). Yet, training value-based methods presents challenges due to the enormous search space inherent to program synthesis. To this end, we propose an initialization protocol for RL agents utilizing pre-trained LMs and a conservative Bellman operator to reduce training complexities. Moreover, we demonstrate how to leverage the learned value functions as a dual strategy to post-process generated programs. Our empirical evaluations demonstrated $\mathcal{B}$-Coder's capability in achieving state-of-the-art performance compared with policy-based methods. Remarkably, this achievement is reached with minimal reward engineering effort, highlighting the effectiveness of value-based RL, independent of reward designs.

Layered State Discovery for Incremental Autonomous Exploration

We study the autonomous exploration (AX) problem proposed by Lim & Auer (2012). In this setting, the objective is to discover a set of $\epsilon$-optimal policies reaching a set $\mathcal{S}_L^{\rightarrow}$ of incrementally $L$-controllable states. We introduce a novel layered decomposition of the set of incrementally $L$-controllable states that is based on the iterative application of a state-expansion operator. We leverage these results to design Layered Autonomous Exploration (LAE), a novel algorithm for AX that attains a sample complexity of $\tilde{\mathcal{O}}(LS^{\rightarrow}_{L(1+\epsilon)}\Gamma_{L(1+\epsilon)} A \ln^{12}(S^{\rightarrow}_{L(1+\epsilon)})/\epsilon^2)$, where $S^{\rightarrow}_{L(1+\epsilon)}$ is the number of states that are incrementally $L(1+\epsilon)$-controllable, $A$ is the number of actions, and $\Gamma_{L(1+\epsilon)}$ is the branching factor of the transitions over such states. LAE improves over the algorithm of Tarbouriech et al. (2020a) by a factor of $L^2$ and it is the first algorithm for AX that works in a countably-infinite state space. Moreover, we show that, under a certain identifiability assumption, LAE achieves minimax-optimal sample complexity of $\tilde{\mathcal{O}}(LS^{\rightarrow}_{L}A\ln^{12}(S^{\rightarrow}_{L})/\epsilon^2)$, outperforming existing algorithms and matching for the first time the lower bound proved by Cai et al. (2022) up to logarithmic factors.

Reaching Goals is Hard: Settling the Sample Complexity of the Stochastic Shortest Path

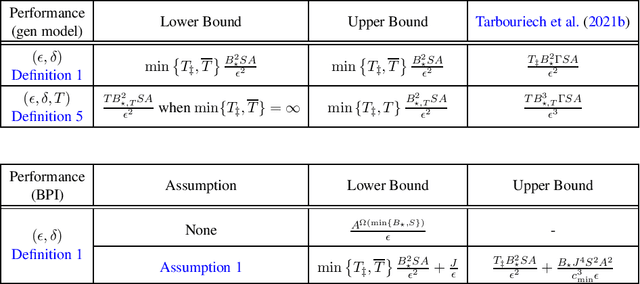
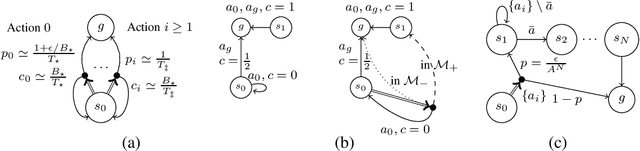
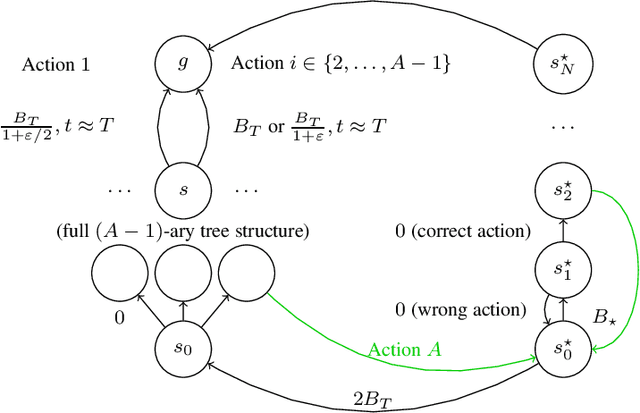
We study the sample complexity of learning an $\epsilon$-optimal policy in the Stochastic Shortest Path (SSP) problem. We first derive sample complexity bounds when the learner has access to a generative model. We show that there exists a worst-case SSP instance with $S$ states, $A$ actions, minimum cost $c_{\min}$, and maximum expected cost of the optimal policy over all states $B_{\star}$, where any algorithm requires at least $\Omega(SAB_{\star}^3/(c_{\min}\epsilon^2))$ samples to return an $\epsilon$-optimal policy with high probability. Surprisingly, this implies that whenever $c_{\min}=0$ an SSP problem may not be learnable, thus revealing that learning in SSPs is strictly harder than in the finite-horizon and discounted settings. We complement this result with lower bounds when prior knowledge of the hitting time of the optimal policy is available and when we restrict optimality by competing against policies with bounded hitting time. Finally, we design an algorithm with matching upper bounds in these cases. This settles the sample complexity of learning $\epsilon$-optimal polices in SSP with generative models. We also initiate the study of learning $\epsilon$-optimal policies without access to a generative model (i.e., the so-called best-policy identification problem), and show that sample-efficient learning is impossible in general. On the other hand, efficient learning can be made possible if we assume the agent can directly reach the goal state from any state by paying a fixed cost. We then establish the first upper and lower bounds under this assumption. Finally, using similar analytic tools, we prove that horizon-free regret is impossible in SSPs under general costs, resolving an open problem in (Tarbouriech et al., 2021c).