Pareto Set Identification With Posterior Sampling

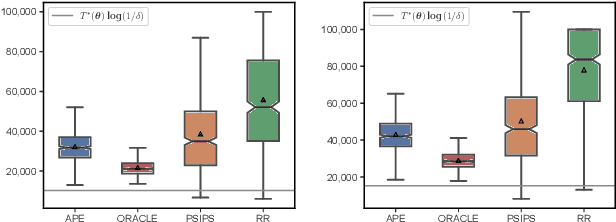
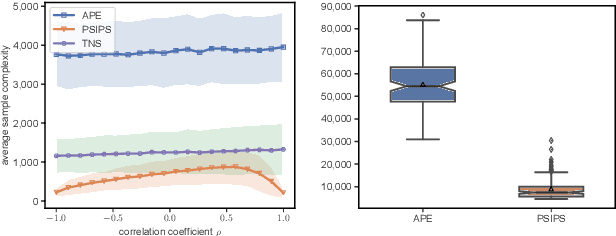
The problem of identifying the best answer among a collection of items having real-valued distribution is well-understood. Despite its practical relevance for many applications, fewer works have studied its extension when multiple and potentially conflicting metrics are available to assess an item's quality. Pareto set identification (PSI) aims to identify the set of answers whose means are not uniformly worse than another. This paper studies PSI in the transductive linear setting with potentially correlated objectives. Building on posterior sampling in both the stopping and the sampling rules, we propose the PSIPS algorithm that deals simultaneously with structure and correlation without paying the computational cost of existing oracle-based algorithms. Both from a frequentist and Bayesian perspective, PSIPS is asymptotically optimal. We demonstrate its good empirical performance in real-world and synthetic instances.

Best-Arm Identification in Unimodal Bandits

We study the fixed-confidence best-arm identification problem in unimodal bandits, in which the means of the arms increase with the index of the arm up to their maximum, then decrease. We derive two lower bounds on the stopping time of any algorithm. The instance-dependent lower bound suggests that due to the unimodal structure, only three arms contribute to the leading confidence-dependent cost. However, a worst-case lower bound shows that a linear dependence on the number of arms is unavoidable in the confidence-independent cost. We propose modifications of Track-and-Stop and a Top Two algorithm that leverage the unimodal structure. Both versions of Track-and-Stop are asymptotically optimal for one-parameter exponential families. The Top Two algorithm is asymptotically near-optimal for Gaussian distributions and we prove a non-asymptotic guarantee matching the worse-case lower bound. The algorithms can be implemented efficiently and we demonstrate their competitive empirical performance.

Optimal Multi-Fidelity Best-Arm Identification

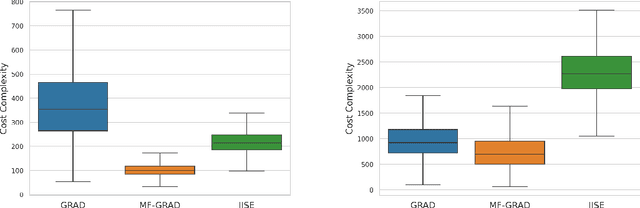
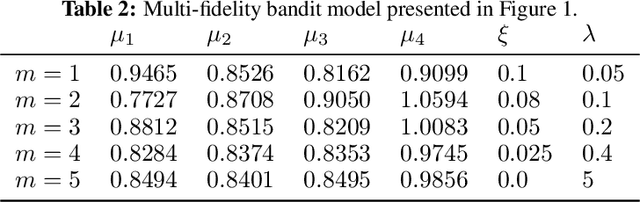
In bandit best-arm identification, an algorithm is tasked with finding the arm with highest mean reward with a specified accuracy as fast as possible. We study multi-fidelity best-arm identification, in which the algorithm can choose to sample an arm at a lower fidelity (less accurate mean estimate) for a lower cost. Several methods have been proposed for tackling this problem, but their optimality remain elusive, notably due to loose lower bounds on the total cost needed to identify the best arm. Our first contribution is a tight, instance-dependent lower bound on the cost complexity. The study of the optimization problem featured in the lower bound provides new insights to devise computationally efficient algorithms, and leads us to propose a gradient-based approach with asymptotically optimal cost complexity. We demonstrate the benefits of the new algorithm compared to existing methods in experiments. Our theoretical and empirical findings also shed light on an intriguing concept of optimal fidelity for each arm.

Power Mean Estimation in Stochastic Monte-Carlo Tree_Search

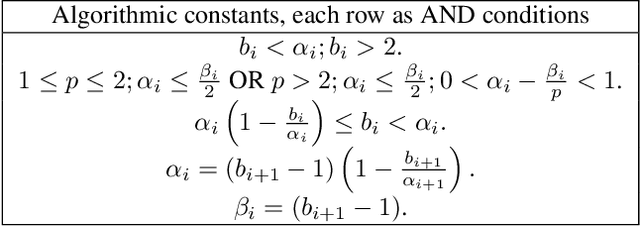
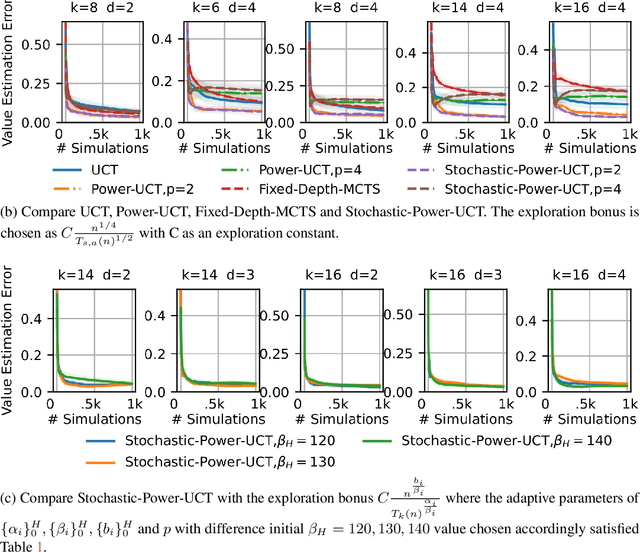
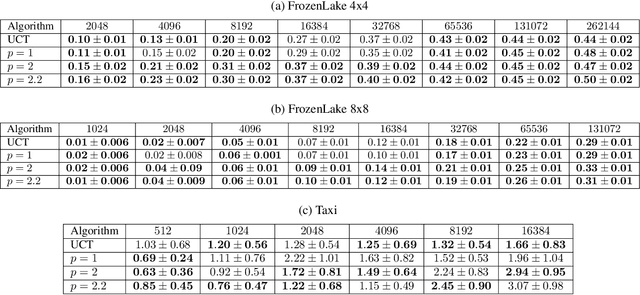
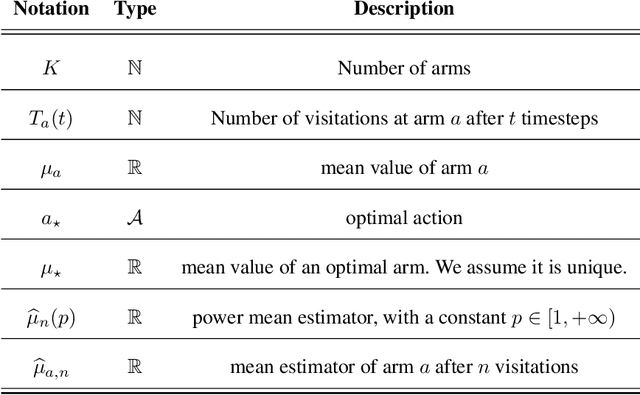
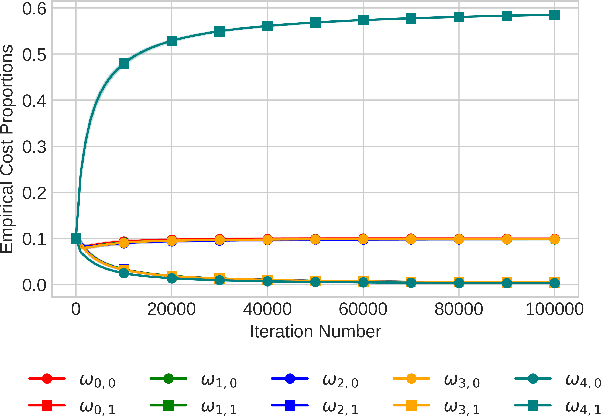
Monte-Carlo Tree Search (MCTS) is a widely-used strategy for online planning that combines Monte-Carlo sampling with forward tree search. Its success relies on the Upper Confidence bound for Trees (UCT) algorithm, an extension of the UCB method for multi-arm bandits. However, the theoretical foundation of UCT is incomplete due to an error in the logarithmic bonus term for action selection, leading to the development of Fixed-Depth-MCTS with a polynomial exploration bonus to balance exploration and exploitation~\citep{shah2022journal}. Both UCT and Fixed-Depth-MCTS suffer from biased value estimation: the weighted sum underestimates the optimal value, while the maximum valuation overestimates it~\citep{coulom2006efficient}. The power mean estimator offers a balanced solution, lying between the average and maximum values. Power-UCT~\citep{dam2019generalized} incorporates this estimator for more accurate value estimates but its theoretical analysis remains incomplete. This paper introduces Stochastic-Power-UCT, an MCTS algorithm using the power mean estimator and tailored for stochastic MDPs. We analyze its polynomial convergence in estimating root node values and show that it shares the same convergence rate of $\mathcal{O}(n^{-1/2})$, with $n$ is the number of visited trajectories, as Fixed-Depth-MCTS, with the latter being a special case of the former. Our theoretical results are validated with empirical tests across various stochastic MDP environments.

Finding good policies in average-reward Markov Decision Processes without prior knowledge

We revisit the identification of an $\varepsilon$-optimal policy in average-reward Markov Decision Processes (MDP). In such MDPs, two measures of complexity have appeared in the literature: the diameter, $D$, and the optimal bias span, $H$, which satisfy $H\leq D$. Prior work have studied the complexity of $\varepsilon$-optimal policy identification only when a generative model is available. In this case, it is known that there exists an MDP with $D \simeq H$ for which the sample complexity to output an $\varepsilon$-optimal policy is $\Omega(SAD/\varepsilon^2)$ where $S$ and $A$ are the sizes of the state and action spaces. Recently, an algorithm with a sample complexity of order $SAH/\varepsilon^2$ has been proposed, but it requires the knowledge of $H$. We first show that the sample complexity required to estimate $H$ is not bounded by any function of $S,A$ and $H$, ruling out the possibility to easily make the previous algorithm agnostic to $H$. By relying instead on a diameter estimation procedure, we propose the first algorithm for $(\varepsilon,\delta)$-PAC policy identification that does not need any form of prior knowledge on the MDP. Its sample complexity scales in $SAD/\varepsilon^2$ in the regime of small $\varepsilon$, which is near-optimal. In the online setting, our first contribution is a lower bound which implies that a sample complexity polynomial in $H$ cannot be achieved in this setting. Then, we propose an online algorithm with a sample complexity in $SAD^2/\varepsilon^2$, as well as a novel approach based on a data-dependent stopping rule that we believe is promising to further reduce this bound.

Bandit Pareto Set Identification: the Fixed Budget Setting

We study a multi-objective pure exploration problem in a multi-armed bandit model. Each arm is associated to an unknown multi-variate distribution and the goal is to identify the distributions whose mean is not uniformly worse than that of another distribution: the Pareto optimal set. We propose and analyze the first algorithms for the \emph{fixed budget} Pareto Set Identification task. We propose Empirical Gap Elimination, a family of algorithms combining a careful estimation of the ``hardness to classify'' each arm in or out of the Pareto set with a generic elimination scheme. We prove that two particular instances, EGE-SR and EGE-SH, have a probability of error that decays exponentially fast with the budget, with an exponent supported by an information theoretic lower-bound. We complement these findings with an empirical study using real-world and synthetic datasets, which showcase the good performance of our algorithms.

Towards Instance-Optimality in Online PAC Reinforcement Learning

Several recent works have proposed instance-dependent upper bounds on the number of episodes needed to identify, with probability $1-\delta$, an $\varepsilon$-optimal policy in finite-horizon tabular Markov Decision Processes (MDPs). These upper bounds feature various complexity measures for the MDP, which are defined based on different notions of sub-optimality gaps. However, as of now, no lower bound has been established to assess the optimality of any of these complexity measures, except for the special case of MDPs with deterministic transitions. In this paper, we propose the first instance-dependent lower bound on the sample complexity required for the PAC identification of a near-optimal policy in any tabular episodic MDP. Additionally, we demonstrate that the sample complexity of the PEDEL algorithm of \cite{Wagenmaker22linearMDP} closely approaches this lower bound. Considering the intractability of PEDEL, we formulate an open question regarding the possibility of achieving our lower bound using a computationally-efficient algorithm.

Adaptive Algorithms for Relaxed Pareto Set Identification

In this paper we revisit the fixed-confidence identification of the Pareto optimal set in a multi-objective multi-armed bandit model. As the sample complexity to identify the exact Pareto set can be very large, a relaxation allowing to output some additional near-optimal arms has been studied. In this work we also tackle alternative relaxations that allow instead to identify a relevant subset of the Pareto set. Notably, we propose a single sampling strategy, called Adaptive Pareto Exploration, that can be used in conjunction with different stopping rules to take into account different relaxations of the Pareto Set Identification problem. We analyze the sample complexity of these different combinations, quantifying in particular the reduction in sample complexity that occurs when one seeks to identify at most $k$ Pareto optimal arms. We showcase the good practical performance of Adaptive Pareto Exploration on a real-world scenario, in which we adaptively explore several vaccination strategies against Covid-19 in order to find the optimal ones when multiple immunogenicity criteria are taken into account.

Active Coverage for PAC Reinforcement Learning

Collecting and leveraging data with good coverage properties plays a crucial role in different aspects of reinforcement learning (RL), including reward-free exploration and offline learning. However, the notion of "good coverage" really depends on the application at hand, as data suitable for one context may not be so for another. In this paper, we formalize the problem of active coverage in episodic Markov decision processes (MDPs), where the goal is to interact with the environment so as to fulfill given sampling requirements. This framework is sufficiently flexible to specify any desired coverage property, making it applicable to any problem that involves online exploration. Our main contribution is an instance-dependent lower bound on the sample complexity of active coverage and a simple game-theoretic algorithm, CovGame, that nearly matches it. We then show that CovGame can be used as a building block to solve different PAC RL tasks. In particular, we obtain a simple algorithm for PAC reward-free exploration with an instance-dependent sample complexity that, in certain MDPs which are "easy to explore", is lower than the minimax one. By further coupling this exploration algorithm with a new technique to do implicit eliminations in policy space, we obtain a computationally-efficient algorithm for best-policy identification whose instance-dependent sample complexity scales with gaps between policy values.

An $\varepsilon$-Best-Arm Identification Algorithm for Fixed-Confidence and Beyond

We propose EB-TC$\varepsilon$, a novel sampling rule for $\varepsilon$-best arm identification in stochastic bandits. It is the first instance of Top Two algorithm analyzed for approximate best arm identification. EB-TC$\varepsilon$ is an *anytime* sampling rule that can therefore be employed without modification for fixed confidence or fixed budget identification (without prior knowledge of the budget). We provide three types of theoretical guarantees for EB-TC$\varepsilon$. First, we prove bounds on its expected sample complexity in the fixed confidence setting, notably showing its asymptotic optimality in combination with an adaptive tuning of its exploration parameter. We complement these findings with upper bounds on its probability of error at any time and for any error parameter, which further yield upper bounds on its simple regret at any time. Finally, we show through numerical simulations that EB-TC$\varepsilon$ performs favorably compared to existing algorithms, in different settings.