Power Mean Estimation in Stochastic Monte-Carlo Tree_Search

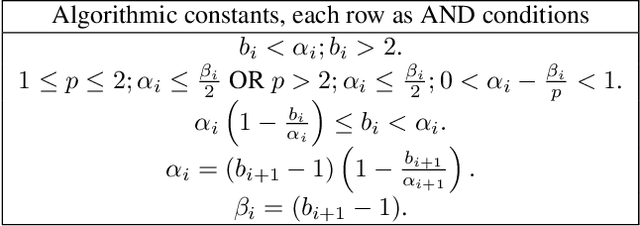
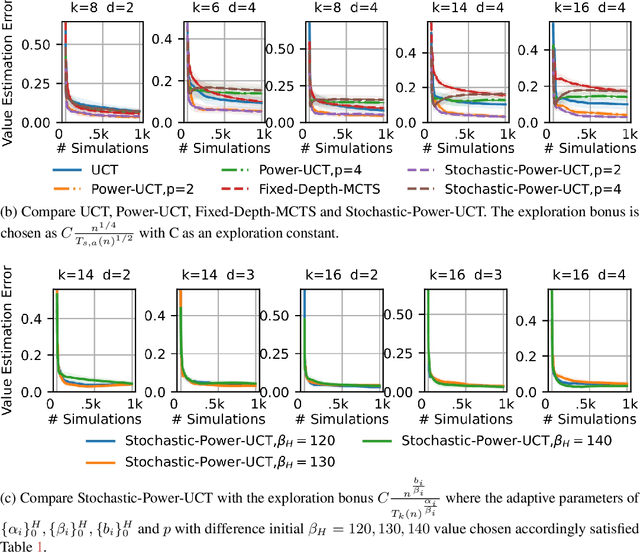
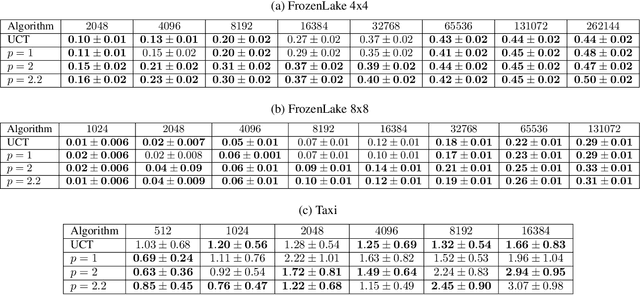
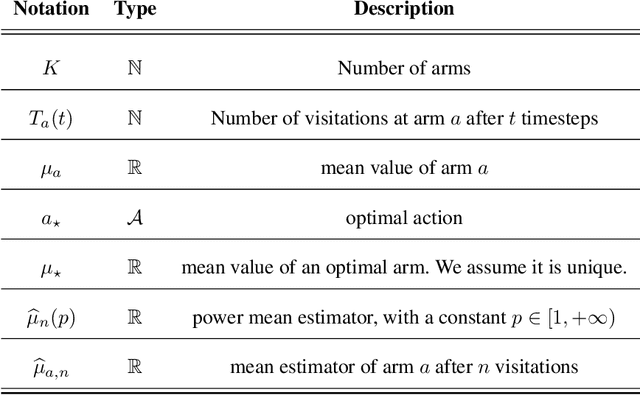
Monte-Carlo Tree Search (MCTS) is a widely-used strategy for online planning that combines Monte-Carlo sampling with forward tree search. Its success relies on the Upper Confidence bound for Trees (UCT) algorithm, an extension of the UCB method for multi-arm bandits. However, the theoretical foundation of UCT is incomplete due to an error in the logarithmic bonus term for action selection, leading to the development of Fixed-Depth-MCTS with a polynomial exploration bonus to balance exploration and exploitation~\citep{shah2022journal}. Both UCT and Fixed-Depth-MCTS suffer from biased value estimation: the weighted sum underestimates the optimal value, while the maximum valuation overestimates it~\citep{coulom2006efficient}. The power mean estimator offers a balanced solution, lying between the average and maximum values. Power-UCT~\citep{dam2019generalized} incorporates this estimator for more accurate value estimates but its theoretical analysis remains incomplete. This paper introduces Stochastic-Power-UCT, an MCTS algorithm using the power mean estimator and tailored for stochastic MDPs. We analyze its polynomial convergence in estimating root node values and show that it shares the same convergence rate of $\mathcal{O}(n^{-1/2})$, with $n$ is the number of visited trajectories, as Fixed-Depth-MCTS, with the latter being a special case of the former. Our theoretical results are validated with empirical tests across various stochastic MDP environments.

Monte-Carlo tree search with uncertainty propagation via optimal transport

This paper introduces a novel backup strategy for Monte-Carlo Tree Search (MCTS) designed for highly stochastic and partially observable Markov decision processes. We adopt a probabilistic approach, modeling both value and action-value nodes as Gaussian distributions. We introduce a novel backup operator that computes value nodes as the Wasserstein barycenter of their action-value children nodes; thus, propagating the uncertainty of the estimate across the tree to the root node. We study our novel backup operator when using a novel combination of $L^1$-Wasserstein barycenter with $\alpha$-divergence, by drawing a notable connection to the generalized mean backup operator. We complement our probabilistic backup operator with two sampling strategies, based on optimistic selection and Thompson sampling, obtaining our Wasserstein MCTS algorithm. We provide theoretical guarantees of asymptotic convergence to the optimal policy, and an empirical evaluation on several stochastic and partially observable environments, where our approach outperforms well-known related baselines.

A Unified Perspective on Value Backup and Exploration in Monte-Carlo Tree Search

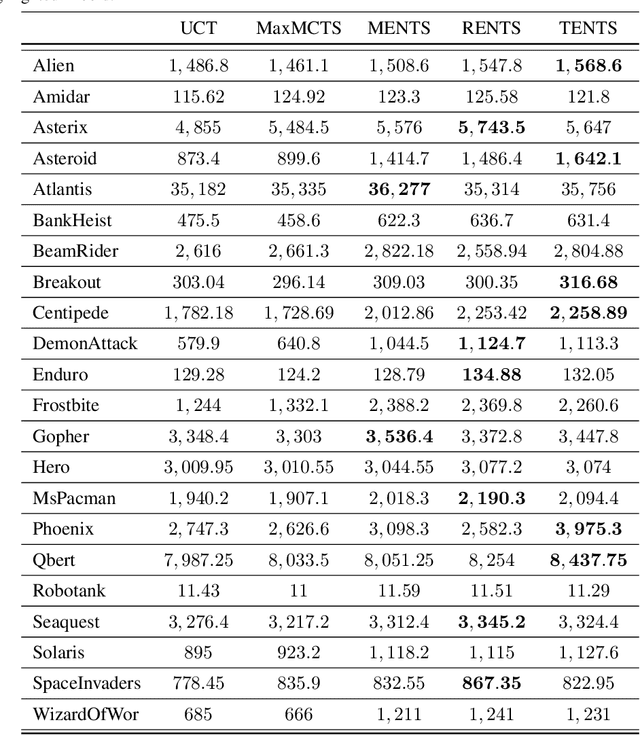
Monte-Carlo Tree Search (MCTS) is a class of methods for solving complex decision-making problems through the synergy of Monte-Carlo planning and Reinforcement Learning (RL). The highly combinatorial nature of the problems commonly addressed by MCTS requires the use of efficient exploration strategies for navigating the planning tree and quickly convergent value backup methods. These crucial problems are particularly evident in recent advances that combine MCTS with deep neural networks for function approximation. In this work, we propose two methods for improving the convergence rate and exploration based on a newly introduced backup operator and entropy regularization. We provide strong theoretical guarantees to bound convergence rate, approximation error, and regret of our methods. Moreover, we introduce a mathematical framework based on the use of the $\alpha$-divergence for backup and exploration in MCTS. We show that this theoretical formulation unifies different approaches, including our newly introduced ones, under the same mathematical framework, allowing to obtain different methods by simply changing the value of $\alpha$. In practice, our unified perspective offers a flexible way to balance between exploration and exploitation by tuning the single $\alpha$ parameter according to the problem at hand. We validate our methods through a rigorous empirical study from basic toy problems to the complex Atari games, and including both MDP and POMDP problems.

Convex Regularization in Monte-Carlo Tree Search

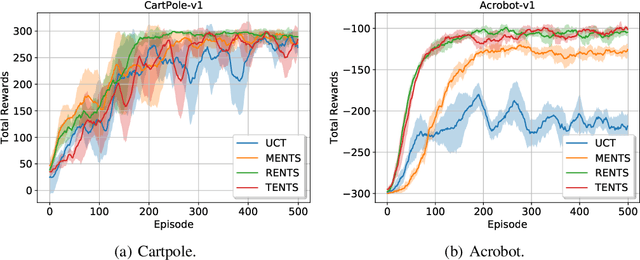
Monte-Carlo planning and Reinforcement Learning (RL) are essential to sequential decision making. The recent AlphaGo and AlphaZero algorithms have shown how to successfully combine these two paradigms in order to solve large scale sequential decision problems. These methodologies exploit a variant of the well-known UCT algorithm to trade off exploitation of good actions and exploration of unvisited states, but their empirical success comes at the cost of poor sample-efficiency and high computation time. In this paper, we overcome these limitations by considering convex regularization in Monte-Carlo Tree Search (MCTS), which has been successfully used in RL to efficiently drive exploration. First, we introduce a unifying theory on the use of generic convex regularizers in MCTS, deriving the regret analysis and providing guarantees of exponential convergence rate. Second, we exploit our theoretical framework to introduce novel regularized backup operators for MCTS, based on the relative entropy of the policy update, and on the Tsallis entropy of the policy. Finally, we empirically evaluate the proposed operators in AlphaGo and AlphaZero on problems of increasing dimensionality and branching factor, from a toy problem to several Atari games, showing their superiority w.r.t. representative baselines.

Generalized Mean Estimation in Monte-Carlo Tree Search

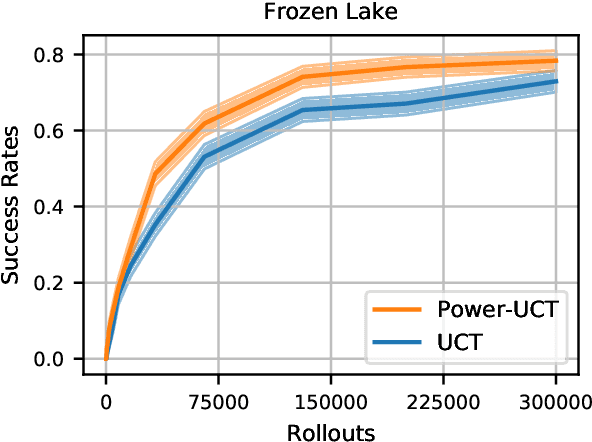
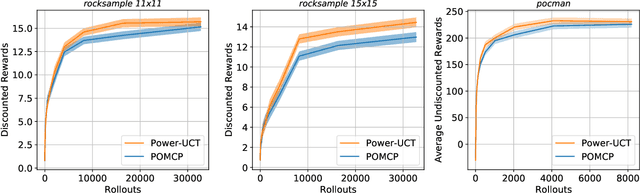
We consider Monte-Carlo Tree Search (MCTS) applied to Markov Decision Processes (MDPs) and Partially Observable MDPs (POMDPs), and the well-known Upper Confidence bound for Trees (UCT) algorithm. In UCT, a tree with nodes (states) and edges (actions) is incrementally built by the expansion of nodes, and the values of nodes are updated through a backup strategy based on the average value of child nodes. However, it has been shown that with enough samples the maximum operator yields more accurate node value estimates than averaging. Instead of settling for one of these value estimates, we go a step further proposing a novel backup strategy which uses the power mean operator, which computes a value between the average and maximum value. We call our new approach Power-UCT and argue how the use of the power mean operator helps to speed up the learning in MCTS. We theoretically analyze our method providing guarantees of convergence to the optimum. Moreover, we discuss a heuristic approach to balance the greediness of backups by tuning the power mean operator according to the number of visits to each node. Finally, we empirically demonstrate the effectiveness of our method in well-known MDP and POMDP benchmarks, showing significant improvement in performance and convergence speed w.r.t. UCT.