Convex Regularization in Monte-Carlo Tree Search
Paper and Code
Jul 01, 2020
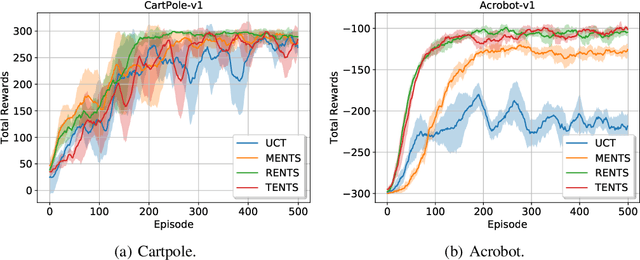
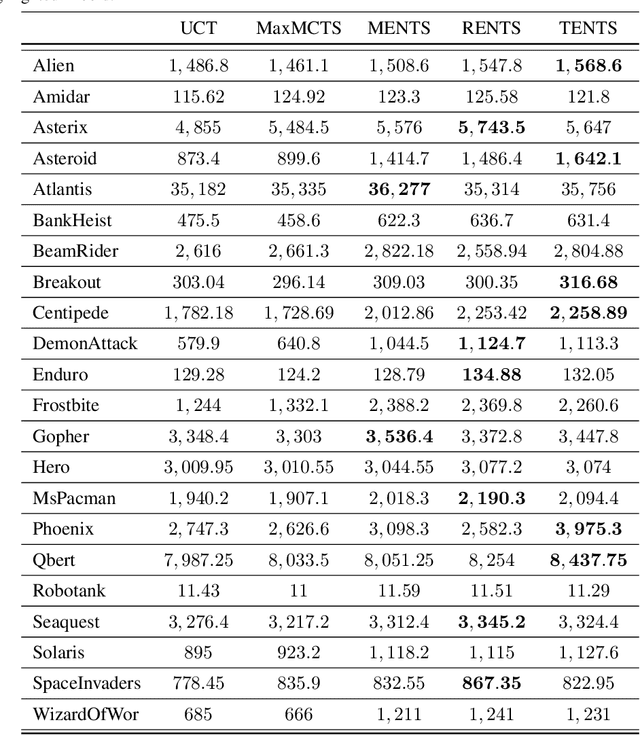
Monte-Carlo planning and Reinforcement Learning (RL) are essential to sequential decision making. The recent AlphaGo and AlphaZero algorithms have shown how to successfully combine these two paradigms in order to solve large scale sequential decision problems. These methodologies exploit a variant of the well-known UCT algorithm to trade off exploitation of good actions and exploration of unvisited states, but their empirical success comes at the cost of poor sample-efficiency and high computation time. In this paper, we overcome these limitations by considering convex regularization in Monte-Carlo Tree Search (MCTS), which has been successfully used in RL to efficiently drive exploration. First, we introduce a unifying theory on the use of generic convex regularizers in MCTS, deriving the regret analysis and providing guarantees of exponential convergence rate. Second, we exploit our theoretical framework to introduce novel regularized backup operators for MCTS, based on the relative entropy of the policy update, and on the Tsallis entropy of the policy. Finally, we empirically evaluate the proposed operators in AlphaGo and AlphaZero on problems of increasing dimensionality and branching factor, from a toy problem to several Atari games, showing their superiority w.r.t. representative baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge