The Batch Complexity of Bandit Pure Exploration

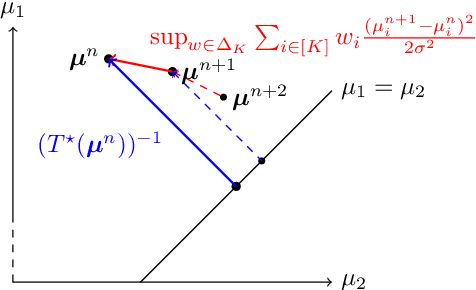
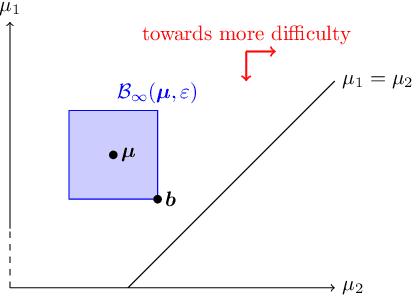
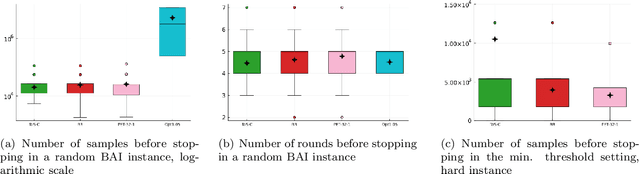
In a fixed-confidence pure exploration problem in stochastic multi-armed bandits, an algorithm iteratively samples arms and should stop as early as possible and return the correct answer to a query about the arms distributions. We are interested in batched methods, which change their sampling behaviour only a few times, between batches of observations. We give an instance-dependent lower bound on the number of batches used by any sample efficient algorithm for any pure exploration task. We then give a general batched algorithm and prove upper bounds on its expected sample complexity and batch complexity. We illustrate both lower and upper bounds on best-arm identification and thresholding bandits.

Finding good policies in average-reward Markov Decision Processes without prior knowledge

We revisit the identification of an $\varepsilon$-optimal policy in average-reward Markov Decision Processes (MDP). In such MDPs, two measures of complexity have appeared in the literature: the diameter, $D$, and the optimal bias span, $H$, which satisfy $H\leq D$. Prior work have studied the complexity of $\varepsilon$-optimal policy identification only when a generative model is available. In this case, it is known that there exists an MDP with $D \simeq H$ for which the sample complexity to output an $\varepsilon$-optimal policy is $\Omega(SAD/\varepsilon^2)$ where $S$ and $A$ are the sizes of the state and action spaces. Recently, an algorithm with a sample complexity of order $SAH/\varepsilon^2$ has been proposed, but it requires the knowledge of $H$. We first show that the sample complexity required to estimate $H$ is not bounded by any function of $S,A$ and $H$, ruling out the possibility to easily make the previous algorithm agnostic to $H$. By relying instead on a diameter estimation procedure, we propose the first algorithm for $(\varepsilon,\delta)$-PAC policy identification that does not need any form of prior knowledge on the MDP. Its sample complexity scales in $SAD/\varepsilon^2$ in the regime of small $\varepsilon$, which is near-optimal. In the online setting, our first contribution is a lower bound which implies that a sample complexity polynomial in $H$ cannot be achieved in this setting. Then, we propose an online algorithm with a sample complexity in $SAD^2/\varepsilon^2$, as well as a novel approach based on a data-dependent stopping rule that we believe is promising to further reduce this bound.

Transfer in Reinforcement Learning via Regret Bounds for Learning Agents

We present an approach for the quantification of the usefulness of transfer in reinforcement learning via regret bounds for a multi-agent setting. Considering a number of $\aleph$ agents operating in the same Markov decision process, however possibly with different reward functions, we consider the regret each agent suffers with respect to an optimal policy maximizing her average reward. We show that when the agents share their observations the total regret of all agents is smaller by a factor of $\sqrt{\aleph}$ compared to the case when each agent has to rely on the information collected by herself. This result demonstrates how considering the regret in multi-agent settings can provide theoretical bounds on the benefit of sharing observations in transfer learning.