Transfer in Reinforcement Learning via Regret Bounds for Learning Agents

We present an approach for the quantification of the usefulness of transfer in reinforcement learning via regret bounds for a multi-agent setting. Considering a number of $\aleph$ agents operating in the same Markov decision process, however possibly with different reward functions, we consider the regret each agent suffers with respect to an optimal policy maximizing her average reward. We show that when the agents share their observations the total regret of all agents is smaller by a factor of $\sqrt{\aleph}$ compared to the case when each agent has to rely on the information collected by herself. This result demonstrates how considering the regret in multi-agent settings can provide theoretical bounds on the benefit of sharing observations in transfer learning.

Autonomous exploration for navigating in non-stationary CMPs

We consider a setting in which the objective is to learn to navigate in a controlled Markov process (CMP) where transition probabilities may abruptly change. For this setting, we propose a performance measure called exploration steps which counts the time steps at which the learner lacks sufficient knowledge to navigate its environment efficiently. We devise a learning meta-algorithm, MNM and prove an upper bound on the exploration steps in terms of the number of changes.

Variational Regret Bounds for Reinforcement Learning

We consider undiscounted reinforcement learning in Markov decision processes (MDPs) where both the reward functions and the state-transition probabilities may vary (gradually or abruptly) over time. For this problem setting, we propose an algorithm and provide performance guarantees for the regret evaluated against the optimal non-stationary policy. The upper bound on the regret is given in terms of the total variation in the MDP. This is the first variational regret bound for the general reinforcement learning setting.

Regret Bounds for Reinforcement Learning via Markov Chain Concentration

We give a simple optimistic algorithm for which it is easy to derive regret bounds of $\tilde{O}(\sqrt{t_{\rm mix} SAT})$ after $T$ steps in uniformly ergodic MDPs with $S$ states, $A$ actions, and mixing time parameter $t_{\rm mix}$. These bounds are the first regret bounds in the general, non-episodic setting with an optimal dependence on all given parameters. They could only be improved by using an alternative mixing time parameter.

Efficient Bias-Span-Constrained Exploration-Exploitation in Reinforcement Learning

We introduce SCAL, an algorithm designed to perform efficient exploration-exploitation in any unknown weakly-communicating Markov decision process (MDP) for which an upper bound $c$ on the span of the optimal bias function is known. For an MDP with $S$ states, $A$ actions and $\Gamma \leq S$ possible next states, we prove a regret bound of $\widetilde{O}(c\sqrt{\Gamma SAT})$, which significantly improves over existing algorithms (e.g., UCRL and PSRL), whose regret scales linearly with the MDP diameter $D$. In fact, the optimal bias span is finite and often much smaller than $D$ (e.g., $D=\infty$ in non-communicating MDPs). A similar result was originally derived by Bartlett and Tewari (2009) for REGAL.C, for which no tractable algorithm is available. In this paper, we relax the optimization problem at the core of REGAL.C, we carefully analyze its properties, and we provide the first computationally efficient algorithm to solve it. Finally, we report numerical simulations supporting our theoretical findings and showing how SCAL significantly outperforms UCRL in MDPs with large diameter and small span.

A Sliding-Window Algorithm for Markov Decision Processes with Arbitrarily Changing Rewards and Transitions

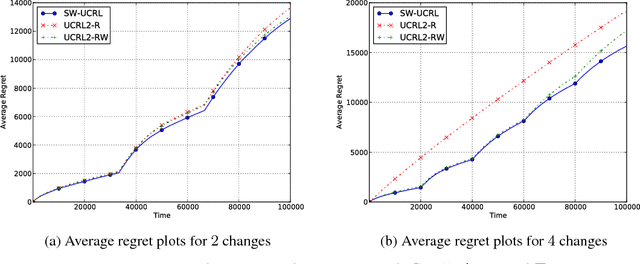
We consider reinforcement learning in changing Markov Decision Processes where both the state-transition probabilities and the reward functions may vary over time. For this problem setting, we propose an algorithm using a sliding window approach and provide performance guarantees for the regret evaluated against the optimal non-stationary policy. We also characterize the optimal window size suitable for our algorithm. These results are complemented by a sample complexity bound on the number of sub-optimal steps taken by the algorithm. Finally, we present some experimental results to support our theoretical analysis.

Selecting Near-Optimal Approximate State Representations in Reinforcement Learning

We consider a reinforcement learning setting introduced in (Maillard et al., NIPS 2011) where the learner does not have explicit access to the states of the underlying Markov decision process (MDP). Instead, she has access to several models that map histories of past interactions to states. Here we improve over known regret bounds in this setting, and more importantly generalize to the case where the models given to the learner do not contain a true model resulting in an MDP representation but only approximations of it. We also give improved error bounds for state aggregation.

Optimal Regret Bounds for Selecting the State Representation in Reinforcement Learning

We consider an agent interacting with an environment in a single stream of actions, observations, and rewards, with no reset. This process is not assumed to be a Markov Decision Process (MDP). Rather, the agent has several representations (mapping histories of past interactions to a discrete state space) of the environment with unknown dynamics, only some of which result in an MDP. The goal is to minimize the average regret criterion against an agent who knows an MDP representation giving the highest optimal reward, and acts optimally in it. Recent regret bounds for this setting are of order $O(T^{2/3})$ with an additive term constant yet exponential in some characteristics of the optimal MDP. We propose an algorithm whose regret after $T$ time steps is $O(\sqrt{T})$, with all constants reasonably small. This is optimal in $T$ since $O(\sqrt{T})$ is the optimal regret in the setting of learning in a (single discrete) MDP.

Online Regret Bounds for Undiscounted Continuous Reinforcement Learning

We derive sublinear regret bounds for undiscounted reinforcement learning in continuous state space. The proposed algorithm combines state aggregation with the use of upper confidence bounds for implementing optimism in the face of uncertainty. Beside the existence of an optimal policy which satisfies the Poisson equation, the only assumptions made are Holder continuity of rewards and transition probabilities.

Regret Bounds for Restless Markov Bandits

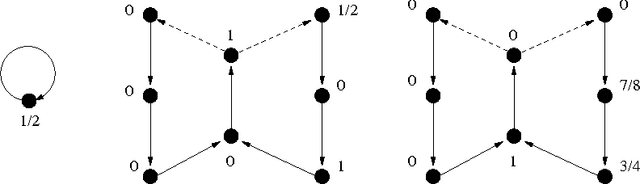
We consider the restless Markov bandit problem, in which the state of each arm evolves according to a Markov process independently of the learner's actions. We suggest an algorithm that after $T$ steps achieves $\tilde{O}(\sqrt{T})$ regret with respect to the best policy that knows the distributions of all arms. No assumptions on the Markov chains are made except that they are irreducible. In addition, we show that index-based policies are necessarily suboptimal for the considered problem.