Autonomous exploration for navigating in non-stationary CMPs

We consider a setting in which the objective is to learn to navigate in a controlled Markov process (CMP) where transition probabilities may abruptly change. For this setting, we propose a performance measure called exploration steps which counts the time steps at which the learner lacks sufficient knowledge to navigate its environment efficiently. We devise a learning meta-algorithm, MNM and prove an upper bound on the exploration steps in terms of the number of changes.

Variational Regret Bounds for Reinforcement Learning

We consider undiscounted reinforcement learning in Markov decision processes (MDPs) where both the reward functions and the state-transition probabilities may vary (gradually or abruptly) over time. For this problem setting, we propose an algorithm and provide performance guarantees for the regret evaluated against the optimal non-stationary policy. The upper bound on the regret is given in terms of the total variation in the MDP. This is the first variational regret bound for the general reinforcement learning setting.

A Sliding-Window Algorithm for Markov Decision Processes with Arbitrarily Changing Rewards and Transitions

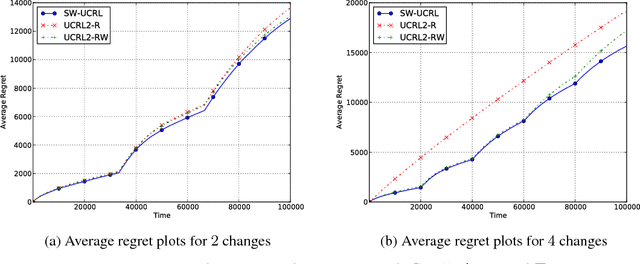
We consider reinforcement learning in changing Markov Decision Processes where both the state-transition probabilities and the reward functions may vary over time. For this problem setting, we propose an algorithm using a sliding window approach and provide performance guarantees for the regret evaluated against the optimal non-stationary policy. We also characterize the optimal window size suitable for our algorithm. These results are complemented by a sample complexity bound on the number of sub-optimal steps taken by the algorithm. Finally, we present some experimental results to support our theoretical analysis.

Online Learning with Randomized Feedback Graphs for Optimal PUE Attacks in Cognitive Radio Networks

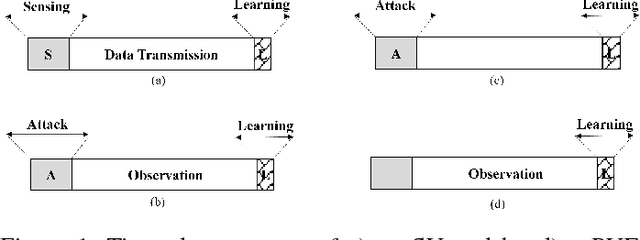
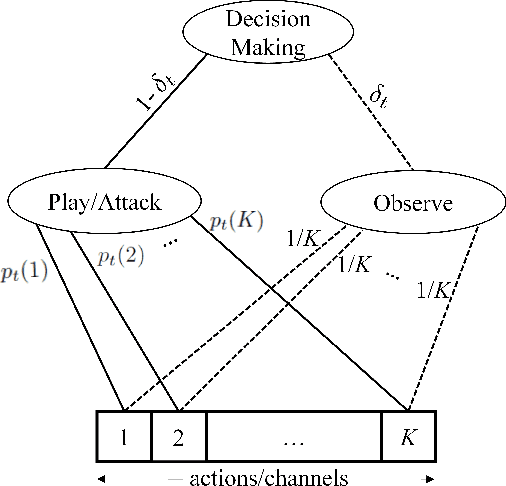
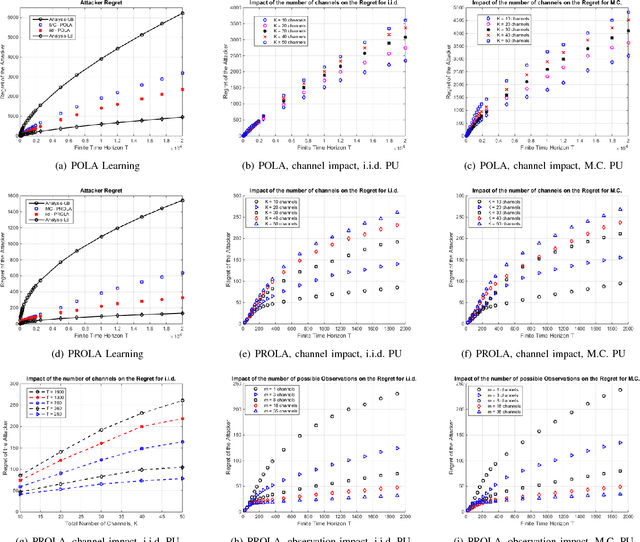
In a cognitive radio network, a secondary user learns the spectrum environment and dynamically accesses the channel where the primary user is inactive. At the same time, a primary user emulation (PUE) attacker can send falsified primary user signals and prevent the secondary user from utilizing the available channel. The best attacking strategies that an attacker can apply have not been well studied. In this paper, for the first time, we study optimal PUE attack strategies by formulating an online learning problem where the attacker needs to dynamically decide the attacking channel in each time slot based on its attacking experience. The challenge in our problem is that since the PUE attack happens in the spectrum sensing phase, the attacker cannot observe the reward on the attacked channel. To address this challenge, we utilize the attacker's observation capability. We propose online learning-based attacking strategies based on the attacker's observation capabilities. Through our analysis, we show that with no observation within the attacking slot, the attacker loses on the regret order, and with the observation of at least one channel, there is a significant improvement on the attacking performance. Observation of multiple channels does not give additional benefit to the attacker (only a constant scaling) though it gives insight on the number of observations required to achieve the minimum constant factor. Our proposed algorithms are optimal in the sense that their regret upper bounds match their corresponding regret lower-bounds. We show consistency between simulation and analytical results under various system parameters.

An algorithm with nearly optimal pseudo-regret for both stochastic and adversarial bandits

We present an algorithm that achieves almost optimal pseudo-regret bounds against adversarial and stochastic bandits. Against adversarial bandits the pseudo-regret is $O(K\sqrt{n \log n})$ and against stochastic bandits the pseudo-regret is $O(\sum_i (\log n)/\Delta_i)$. We also show that no algorithm with $O(\log n)$ pseudo-regret against stochastic bandits can achieve $\tilde{O}(\sqrt{n})$ expected regret against adaptive adversarial bandits. This complements previous results of Bubeck and Slivkins (2012) that show $\tilde{O}(\sqrt{n})$ expected adversarial regret with $O((\log n)^2)$ stochastic pseudo-regret.

Upper-Confidence-Bound Algorithms for Active Learning in Multi-Armed Bandits

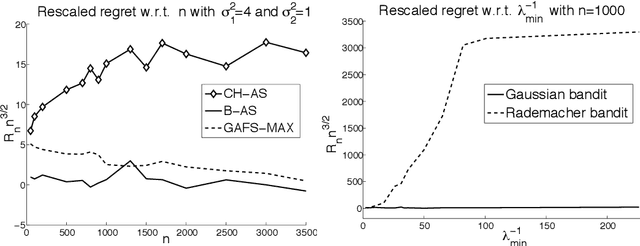
In this paper, we study the problem of estimating uniformly well the mean values of several distributions given a finite budget of samples. If the variance of the distributions were known, one could design an optimal sampling strategy by collecting a number of independent samples per distribution that is proportional to their variance. However, in the more realistic case where the distributions are not known in advance, one needs to design adaptive sampling strategies in order to select which distribution to sample from according to the previously observed samples. We describe two strategies based on pulling the distributions a number of times that is proportional to a high-probability upper-confidence-bound on their variance (built from previous observed samples) and report a finite-sample performance analysis on the excess estimation error compared to the optimal allocation. We show that the performance of these allocation strategies depends not only on the variances but also on the full shape of the distributions.

PinView: Implicit Feedback in Content-Based Image Retrieval

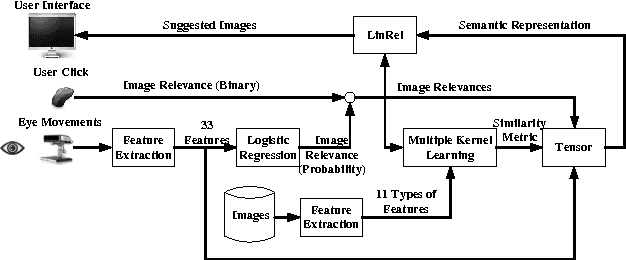
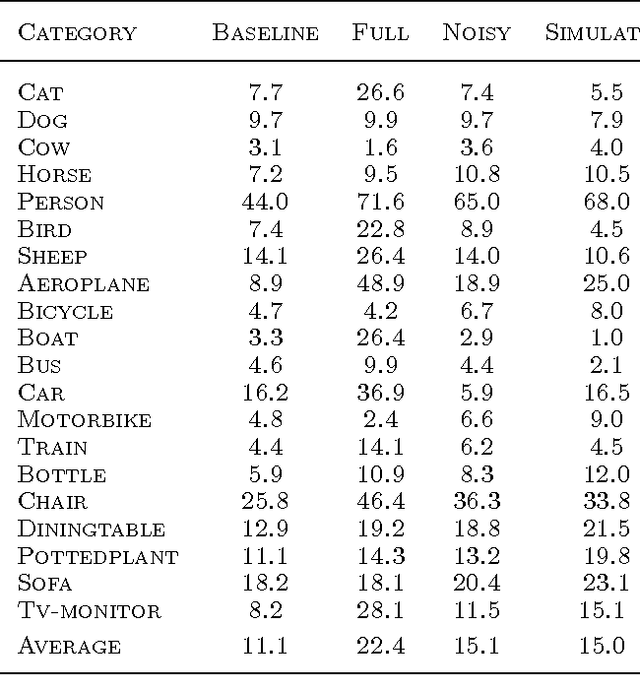
This paper describes PinView, a content-based image retrieval system that exploits implicit relevance feedback collected during a search session. PinView contains several novel methods to infer the intent of the user. From relevance feedback, such as eye movements or pointer clicks, and visual features of images, PinView learns a similarity metric between images which depends on the current interests of the user. It then retrieves images with a specialized online learning algorithm that balances the tradeoff between exploring new images and exploiting the already inferred interests of the user. We have integrated PinView to the content-based image retrieval system PicSOM, which enables applying PinView to real-world image databases. With the new algorithms PinView outperforms the original PicSOM, and in online experiments with real users the combination of implicit and explicit feedback gives the best results.

Regret Bounds for Restless Markov Bandits

We consider the restless Markov bandit problem, in which the state of each arm evolves according to a Markov process independently of the learner's actions. We suggest an algorithm that after $T$ steps achieves $\tilde{O}(\sqrt{T})$ regret with respect to the best policy that knows the distributions of all arms. No assumptions on the Markov chains are made except that they are irreducible. In addition, we show that index-based policies are necessarily suboptimal for the considered problem.

PAC-Bayesian Inequalities for Martingales

We present a set of high-probability inequalities that control the concentration of weighted averages of multiple (possibly uncountably many) simultaneously evolving and interdependent martingales. Our results extend the PAC-Bayesian analysis in learning theory from the i.i.d. setting to martingales opening the way for its application to importance weighted sampling, reinforcement learning, and other interactive learning domains, as well as many other domains in probability theory and statistics, where martingales are encountered. We also present a comparison inequality that bounds the expectation of a convex function of a martingale difference sequence shifted to the [0,1] interval by the expectation of the same function of independent Bernoulli variables. This inequality is applied to derive a tighter analog of Hoeffding-Azuma's inequality.

Noisy Search with Comparative Feedback

We present theoretical results in terms of lower and upper bounds on the query complexity of noisy search with comparative feedback. In this search model, the noise in the feedback depends on the distance between query points and the search target. Consequently, the error probability in the feedback is not fixed but varies for the queries posed by the search algorithm. Our results show that a target out of n items can be found in O(log n) queries. We also show the surprising result that for k possible answers per query, the speedup is not log k (as for k-ary search) but only log log k in some cases.