Chao-Kai Chiang
LLM Routing with Dueling Feedback
Oct 01, 2025Abstract:We study LLM routing, the problem of selecting the best model for each query while balancing user satisfaction, model expertise, and inference cost. We formulate routing as contextual dueling bandits, learning from pairwise preference feedback rather than absolute scores, thereby yielding label-efficient and dynamic adaptation. Building on this formulation, we introduce Category-Calibrated Fine-Tuning (CCFT), a representation-learning method that derives model embeddings from offline data using contrastive fine-tuning with categorical weighting. These embeddings enable the practical instantiation of Feel-Good Thompson Sampling for Contextual Dueling Bandits (FGTS.CDB), a theoretically grounded posterior-sampling algorithm. We propose four variants of the categorical weighting that explicitly integrate model quality and cost, and we empirically evaluate the proposed methods on the RouterBench and MixInstruct datasets. Across both benchmarks, our methods achieve lower cumulative regret and faster convergence, with better robustness and performance-cost balance than strong baselines built with a general-purpose OpenAI embedding model.
Domain Adaptation and Entanglement: an Optimal Transport Perspective
Mar 11, 2025
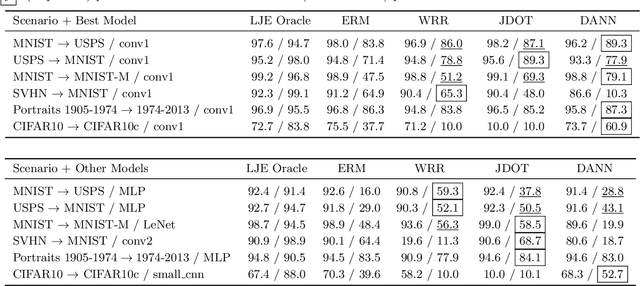

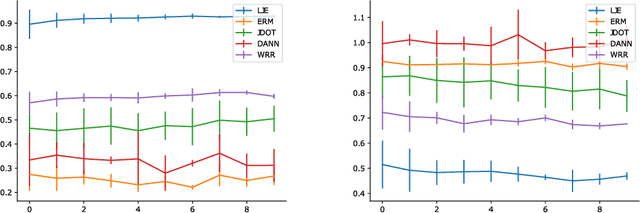
Abstract:Current machine learning systems are brittle in the face of distribution shifts (DS), where the target distribution that the system is tested on differs from the source distribution used to train the system. This problem of robustness to DS has been studied extensively in the field of domain adaptation. For deep neural networks, a popular framework for unsupervised domain adaptation (UDA) is domain matching, in which algorithms try to align the marginal distributions in the feature or output space. The current theoretical understanding of these methods, however, is limited and existing theoretical results are not precise enough to characterize their performance in practice. In this paper, we derive new bounds based on optimal transport that analyze the UDA problem. Our new bounds include a term which we dub as \emph{entanglement}, consisting of an expectation of Wasserstein distance between conditionals with respect to changing data distributions. Analysis of the entanglement term provides a novel perspective on the unoptimizable aspects of UDA. In various experiments with multiple models across several DS scenarios, we show that this term can be used to explain the varying performance of UDA algorithms.
Unified Risk Analysis for Weakly Supervised Learning
Sep 15, 2023



Abstract:Among the flourishing research of weakly supervised learning (WSL), we recognize the lack of a unified interpretation of the mechanism behind the weakly supervised scenarios, let alone a systematic treatment of the risk rewrite problem, a crucial step in the empirical risk minimization approach. In this paper, we introduce a framework providing a comprehensive understanding and a unified methodology for WSL. The formulation component of the framework, leveraging a contamination perspective, provides a unified interpretation of how weak supervision is formed and subsumes fifteen existing WSL settings. The induced reduction graphs offer comprehensive connections over WSLs. The analysis component of the framework, viewed as a decontamination process, provides a systematic method of conducting risk rewrite. In addition to the conventional inverse matrix approach, we devise a novel strategy called marginal chain aiming to decontaminate distributions. We justify the feasibility of the proposed framework by recovering existing rewrites reported in the literature.
Asymptotically Optimal Thompson Sampling Based Policy for the Uniform Bandits and the Gaussian Bandits
Feb 28, 2023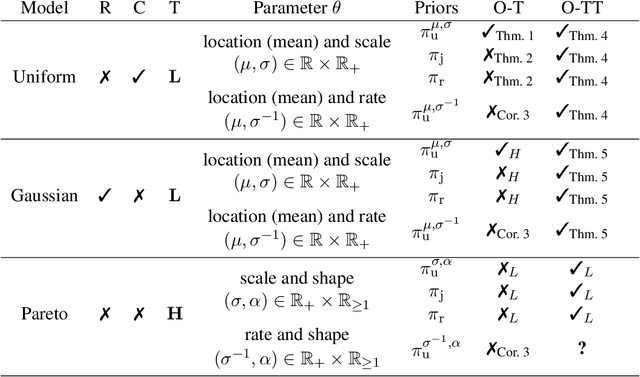



Abstract:Thompson sampling (TS) for the parametric stochastic multi-armed bandits has been well studied under the one-dimensional parametric models. It is often reported that TS is fairly insensitive to the choice of the prior when it comes to regret bounds. However, this property is not necessarily true when multiparameter models are considered, e.g., a Gaussian model with unknown mean and variance parameters. In this paper, we first extend the regret analysis of TS to the model of uniform distributions with unknown supports. Specifically, we show that a switch of noninformative priors drastically affects the regret in expectation. Through our analysis, the uniform prior is proven to be the optimal choice in terms of the expected regret, while the reference prior and the Jeffreys prior are found to be suboptimal, which is consistent with previous findings in the model of Gaussian distributions. However, the uniform prior is specific to the parameterization of the distributions, meaning that if an agent considers different parameterizations of the same model, the agent with the uniform prior might not always achieve the optimal performance. In light of this limitation, we propose a slightly modified TS-based policy, called TS with Truncation (TS-T), which can achieve the asymptotic optimality for the Gaussian distributions and the uniform distributions by using the reference prior and the Jeffreys prior that are invariant under one-to-one reparameterizations. The pre-processig of the posterior distribution is the key to TS-T, where we add an adaptive truncation procedure on the parameter space of the posterior distributions. Simulation results support our analysis, where TS-T shows the best performance in a finite-time horizon compared to other known optimal policies, while TS with the invariant priors performs poorly.
Optimality of Thompson Sampling with Noninformative Priors for Pareto Bandits
Feb 03, 2023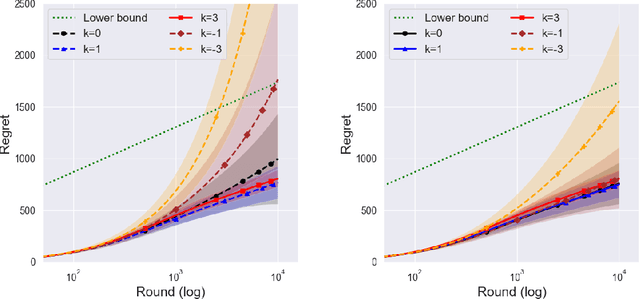
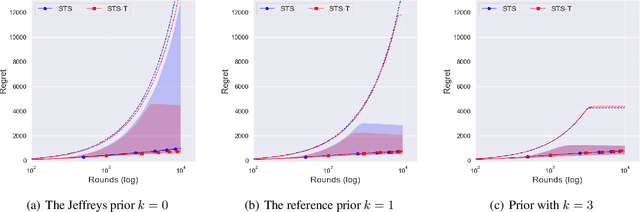

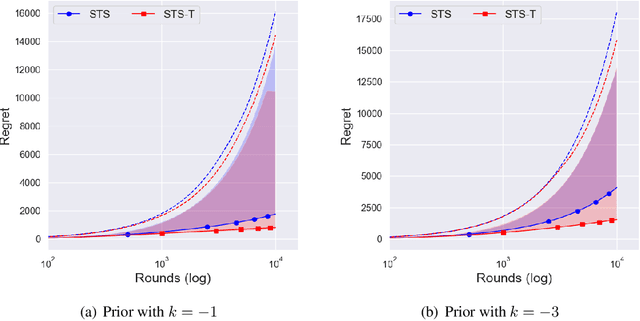
Abstract:In the stochastic multi-armed bandit problem, a randomized probability matching policy called Thompson sampling (TS) has shown excellent performance in various reward models. In addition to the empirical performance, TS has been shown to achieve asymptotic problem-dependent lower bounds in several models. However, its optimality has been mainly addressed under light-tailed or one-parameter models that belong to exponential families. In this paper, we consider the optimality of TS for the Pareto model that has a heavy tail and is parameterized by two unknown parameters. Specifically, we discuss the optimality of TS with probability matching priors that include the Jeffreys prior and the reference priors. We first prove that TS with certain probability matching priors can achieve the optimal regret bound. Then, we show the suboptimality of TS with other priors, including the Jeffreys and the reference priors. Nevertheless, we find that TS with the Jeffreys and reference priors can achieve the asymptotic lower bound if one uses a truncation procedure. These results suggest carefully choosing noninformative priors to avoid suboptimality and show the effectiveness of truncation procedures in TS-based policies.
Hyper-parameter Tuning under a Budget Constraint
Feb 01, 2019
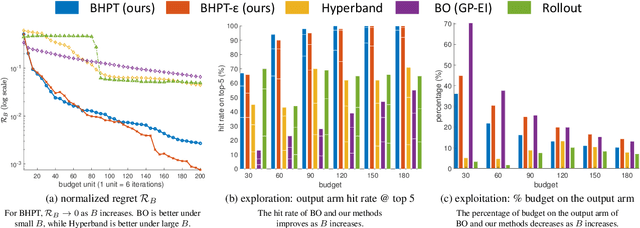
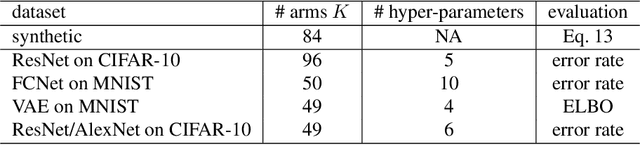
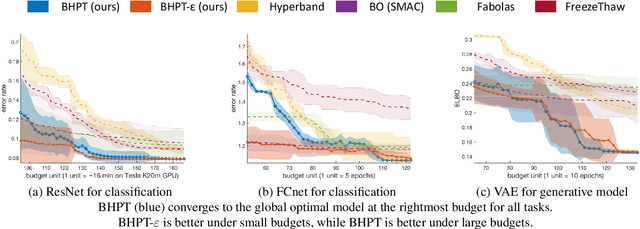
Abstract:We study a budgeted hyper-parameter tuning problem, where we optimize the tuning result under a hard resource constraint. We propose to solve it as a sequential decision making problem, such that we can use the partial training progress of configurations to dynamically allocate the remaining budget. Our algorithm combines a Bayesian belief model which estimates the future performance of configurations, with an action-value function which balances exploration-exploitation tradeoff, to optimize the final output. It automatically adapts the tuning behaviors to different constraints, which is useful in practice. Experiment results demonstrate superior performance over existing algorithms, including the-state-of-the-art one, on real-world tuning tasks across a range of different budgets.
Federated Multi-Task Learning
Feb 27, 2018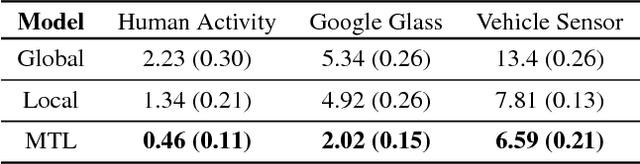



Abstract:Federated learning poses new statistical and systems challenges in training machine learning models over distributed networks of devices. In this work, we show that multi-task learning is naturally suited to handle the statistical challenges of this setting, and propose a novel systems-aware optimization method, MOCHA, that is robust to practical systems issues. Our method and theory for the first time consider issues of high communication cost, stragglers, and fault tolerance for distributed multi-task learning. The resulting method achieves significant speedups compared to alternatives in the federated setting, as we demonstrate through simulations on real-world federated datasets.
An algorithm with nearly optimal pseudo-regret for both stochastic and adversarial bandits
May 27, 2016Abstract:We present an algorithm that achieves almost optimal pseudo-regret bounds against adversarial and stochastic bandits. Against adversarial bandits the pseudo-regret is $O(K\sqrt{n \log n})$ and against stochastic bandits the pseudo-regret is $O(\sum_i (\log n)/\Delta_i)$. We also show that no algorithm with $O(\log n)$ pseudo-regret against stochastic bandits can achieve $\tilde{O}(\sqrt{n})$ expected regret against adaptive adversarial bandits. This complements previous results of Bubeck and Slivkins (2012) that show $\tilde{O}(\sqrt{n})$ expected adversarial regret with $O((\log n)^2)$ stochastic pseudo-regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge