HEEGNet: Hyperbolic Embeddings for EEG

Electroencephalography (EEG)-based brain-computer interfaces facilitate direct communication with a computer, enabling promising applications in human-computer interactions. However, their utility is currently limited because EEG decoding often suffers from poor generalization due to distribution shifts across domains (e.g., subjects). Learning robust representations that capture underlying task-relevant information would mitigate these shifts and improve generalization. One promising approach is to exploit the underlying hierarchical structure in EEG, as recent studies suggest that hierarchical cognitive processes, such as visual processing, can be encoded in EEG. While many decoding methods still rely on Euclidean embeddings, recent work has begun exploring hyperbolic geometry for EEG. Hyperbolic spaces, regarded as the continuous analogue of tree structures, provide a natural geometry for representing hierarchical data. In this study, we first empirically demonstrate that EEG data exhibit hyperbolicity and show that hyperbolic embeddings improve generalization. Motivated by these findings, we propose HEEGNet, a hybrid hyperbolic network architecture to capture the hierarchical structure in EEG and learn domain-invariant hyperbolic embeddings. To this end, HEEGNet combines both Euclidean and hyperbolic encoders and employs a novel coarse-to-fine domain adaptation strategy. Extensive experiments on multiple public EEG datasets, covering visual evoked potentials, emotion recognition, and intracranial EEG, demonstrate that HEEGNet achieves state-of-the-art performance.

Domain Adaptation and Entanglement: an Optimal Transport Perspective

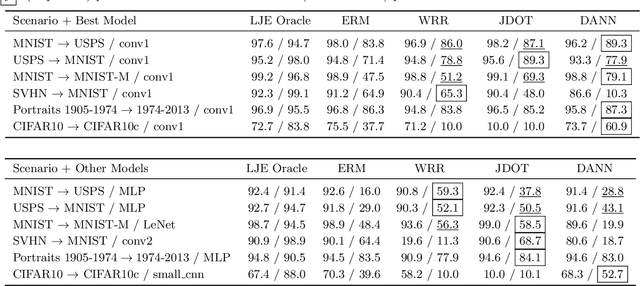
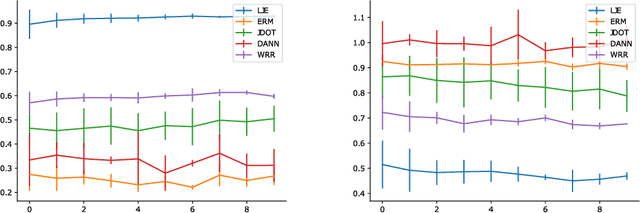
Current machine learning systems are brittle in the face of distribution shifts (DS), where the target distribution that the system is tested on differs from the source distribution used to train the system. This problem of robustness to DS has been studied extensively in the field of domain adaptation. For deep neural networks, a popular framework for unsupervised domain adaptation (UDA) is domain matching, in which algorithms try to align the marginal distributions in the feature or output space. The current theoretical understanding of these methods, however, is limited and existing theoretical results are not precise enough to characterize their performance in practice. In this paper, we derive new bounds based on optimal transport that analyze the UDA problem. Our new bounds include a term which we dub as \emph{entanglement}, consisting of an expectation of Wasserstein distance between conditionals with respect to changing data distributions. Analysis of the entanglement term provides a novel perspective on the unoptimizable aspects of UDA. In various experiments with multiple models across several DS scenarios, we show that this term can be used to explain the varying performance of UDA algorithms.