Follow-the-Perturbed-Leader with Fréchet-type Tail Distributions: Optimality in Adversarial Bandits and Best-of-Both-Worlds

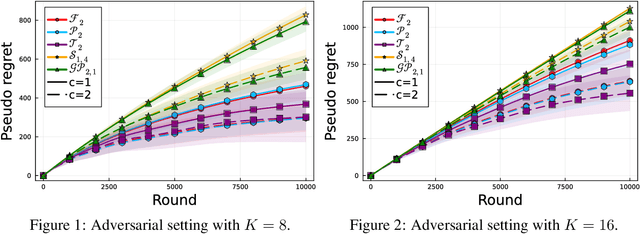
This paper studies the optimality of the Follow-the-Perturbed-Leader (FTPL) policy in both adversarial and stochastic $K$-armed bandits. Despite the widespread use of the Follow-the-Regularized-Leader (FTRL) framework with various choices of regularization, the FTPL framework, which relies on random perturbations, has not received much attention, despite its inherent simplicity. In adversarial bandits, there has been conjecture that FTPL could potentially achieve $\mathcal{O}(\sqrt{KT})$ regrets if perturbations follow a distribution with a Fr\'{e}chet-type tail. Recent work by Honda et al. (2023) showed that FTPL with Fr\'{e}chet distribution with shape $\alpha=2$ indeed attains this bound and, notably logarithmic regret in stochastic bandits, meaning the Best-of-Both-Worlds (BOBW) capability of FTPL. However, this result only partly resolves the above conjecture because their analysis heavily relies on the specific form of the Fr\'{e}chet distribution with this shape. In this paper, we establish a sufficient condition for perturbations to achieve $\mathcal{O}(\sqrt{KT})$ regrets in the adversarial setting, which covers, e.g., Fr\'{e}chet, Pareto, and Student-$t$ distributions. We also demonstrate the BOBW achievability of FTPL with certain Fr\'{e}chet-type tail distributions. Our results contribute not only to resolving existing conjectures through the lens of extreme value theory but also potentially offer insights into the effect of the regularization functions in FTRL through the mapping from FTPL to FTRL.

Thompson Exploration with Best Challenger Rule in Best Arm Identification

This paper studies the fixed-confidence best arm identification (BAI) problem in the bandit framework in the canonical single-parameter exponential models. For this problem, many policies have been proposed, but most of them require solving an optimization problem at every round and/or are forced to explore an arm at least a certain number of times except those restricted to the Gaussian model. To address these limitations, we propose a novel policy that combines Thompson sampling with a computationally efficient approach known as the best challenger rule. While Thompson sampling was originally considered for maximizing the cumulative reward, we demonstrate that it can be used to naturally explore arms in BAI without forcing it. We show that our policy is asymptotically optimal for any two-armed bandit problems and achieves near optimality for general $K$-armed bandit problems for $K\geq 3$. Nevertheless, in numerical experiments, our policy shows competitive performance compared to asymptotically optimal policies in terms of sample complexity while requiring less computation cost. In addition, we highlight the advantages of our policy by comparing it to the concept of $\beta$-optimality, a relaxed notion of asymptotic optimality commonly considered in the analysis of a class of policies including the proposed one.

Asymptotically Optimal Thompson Sampling Based Policy for the Uniform Bandits and the Gaussian Bandits

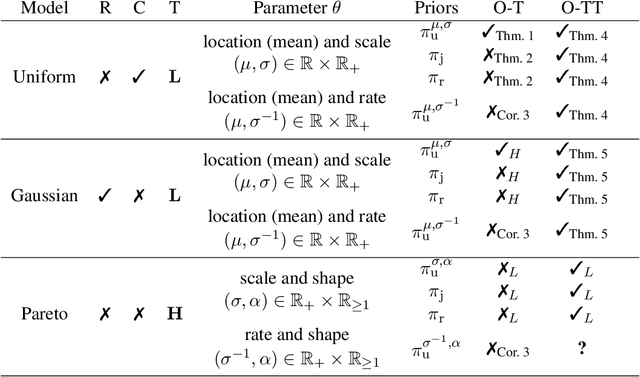
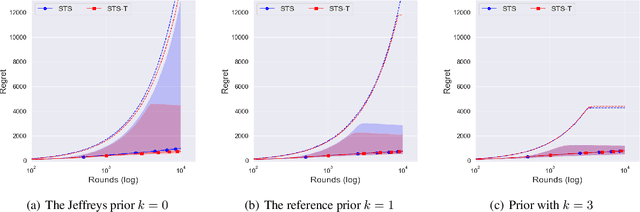
Thompson sampling (TS) for the parametric stochastic multi-armed bandits has been well studied under the one-dimensional parametric models. It is often reported that TS is fairly insensitive to the choice of the prior when it comes to regret bounds. However, this property is not necessarily true when multiparameter models are considered, e.g., a Gaussian model with unknown mean and variance parameters. In this paper, we first extend the regret analysis of TS to the model of uniform distributions with unknown supports. Specifically, we show that a switch of noninformative priors drastically affects the regret in expectation. Through our analysis, the uniform prior is proven to be the optimal choice in terms of the expected regret, while the reference prior and the Jeffreys prior are found to be suboptimal, which is consistent with previous findings in the model of Gaussian distributions. However, the uniform prior is specific to the parameterization of the distributions, meaning that if an agent considers different parameterizations of the same model, the agent with the uniform prior might not always achieve the optimal performance. In light of this limitation, we propose a slightly modified TS-based policy, called TS with Truncation (TS-T), which can achieve the asymptotic optimality for the Gaussian distributions and the uniform distributions by using the reference prior and the Jeffreys prior that are invariant under one-to-one reparameterizations. The pre-processig of the posterior distribution is the key to TS-T, where we add an adaptive truncation procedure on the parameter space of the posterior distributions. Simulation results support our analysis, where TS-T shows the best performance in a finite-time horizon compared to other known optimal policies, while TS with the invariant priors performs poorly.

Optimality of Thompson Sampling with Noninformative Priors for Pareto Bandits

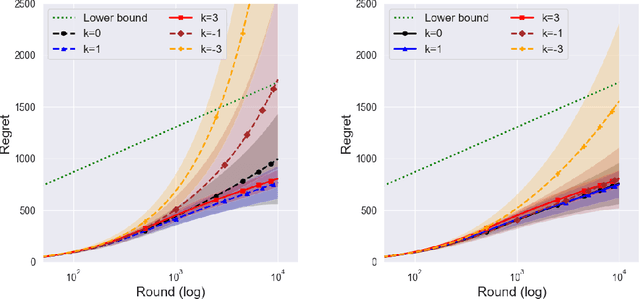
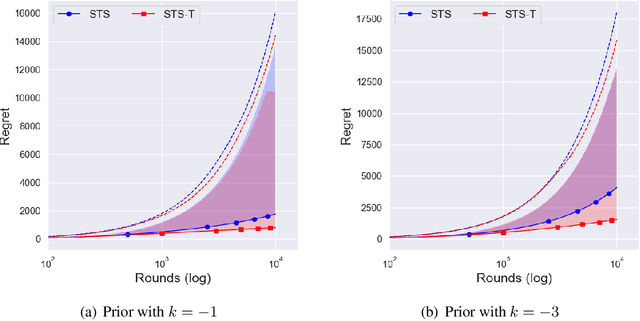
In the stochastic multi-armed bandit problem, a randomized probability matching policy called Thompson sampling (TS) has shown excellent performance in various reward models. In addition to the empirical performance, TS has been shown to achieve asymptotic problem-dependent lower bounds in several models. However, its optimality has been mainly addressed under light-tailed or one-parameter models that belong to exponential families. In this paper, we consider the optimality of TS for the Pareto model that has a heavy tail and is parameterized by two unknown parameters. Specifically, we discuss the optimality of TS with probability matching priors that include the Jeffreys prior and the reference priors. We first prove that TS with certain probability matching priors can achieve the optimal regret bound. Then, we show the suboptimality of TS with other priors, including the Jeffreys and the reference priors. Nevertheless, we find that TS with the Jeffreys and reference priors can achieve the asymptotic lower bound if one uses a truncation procedure. These results suggest carefully choosing noninformative priors to avoid suboptimality and show the effectiveness of truncation procedures in TS-based policies.

A Symmetric Loss Perspective of Reliable Machine Learning

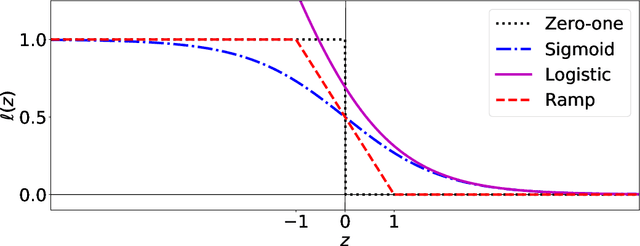
When minimizing the empirical risk in binary classification, it is a common practice to replace the zero-one loss with a surrogate loss to make the learning objective feasible to optimize. Examples of well-known surrogate losses for binary classification include the logistic loss, hinge loss, and sigmoid loss. It is known that the choice of a surrogate loss can highly influence the performance of the trained classifier and therefore it should be carefully chosen. Recently, surrogate losses that satisfy a certain symmetric condition (aka., symmetric losses) have demonstrated their usefulness in learning from corrupted labels. In this article, we provide an overview of symmetric losses and their applications. First, we review how a symmetric loss can yield robust classification from corrupted labels in balanced error rate (BER) minimization and area under the receiver operating characteristic curve (AUC) maximization. Then, we demonstrate how the robust AUC maximization method can benefit natural language processing in the problem where we want to learn only from relevant keywords and unlabeled documents. Finally, we conclude this article by discussing future directions, including potential applications of symmetric losses for reliable machine learning and the design of non-symmetric losses that can benefit from the symmetric condition.

Learning Only from Relevant Keywords and Unlabeled Documents

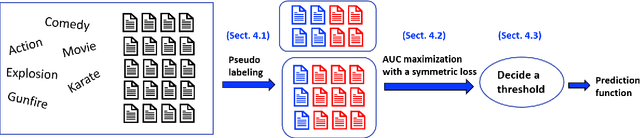
We consider a document classification problem where document labels are absent but only relevant keywords of a target class and unlabeled documents are given. Although heuristic methods based on pseudo-labeling have been considered, theoretical understanding of this problem has still been limited. Moreover, previous methods cannot easily incorporate well-developed techniques in supervised text classification. In this paper, we propose a theoretically guaranteed learning framework that is simple to implement and has flexible choices of models, e.g., linear models or neural networks. We demonstrate how to optimize the area under the receiver operating characteristic curve (AUC) effectively and also discuss how to adjust it to optimize other well-known evaluation metrics such as the accuracy and F1-measure. Finally, we show the effectiveness of our framework using benchmark datasets.

Domain Discrepancy Measure Using Complex Models in Unsupervised Domain Adaptation

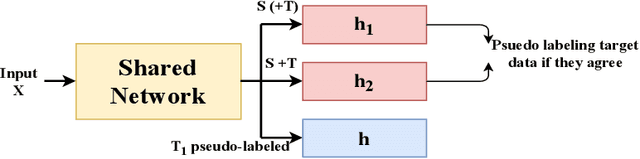
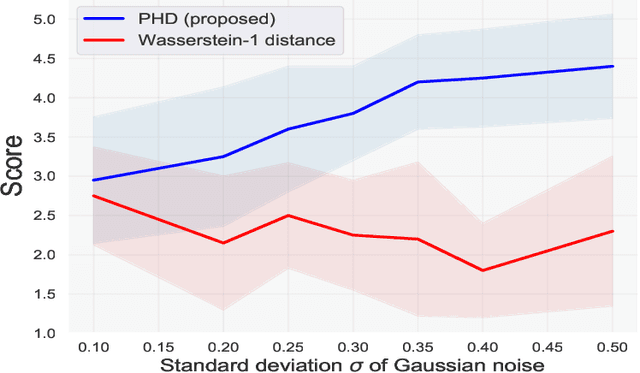
We address the problem of measuring the difference between two domains in unsupervised domain adaptation. We point out that the existing discrepancy measures are less informative when complex models such as deep neural networks are applied. Furthermore, estimation of the existing discrepancy measures can be computationally difficult and only limited to the binary classification task. To mitigate these shortcomings, we propose a novel discrepancy measure that is very simple to estimate for many tasks not limited to binary classification, theoretically-grounded, and can be applied effectively for complex models. We also provide easy-to-interpret generalization bounds that explain the effectiveness of a family of pseudo-labeling methods in unsupervised domain adaptation. Finally, we conduct experiments to validate the usefulness of our proposed discrepancy measure.

On Symmetric Losses for Learning from Corrupted Labels

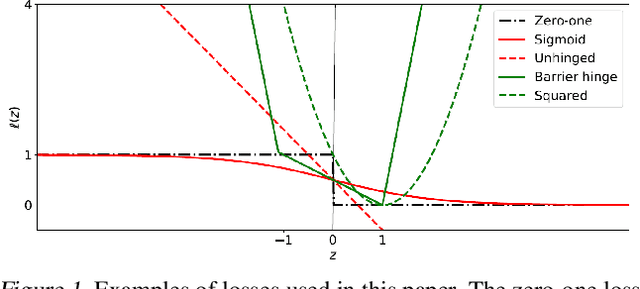
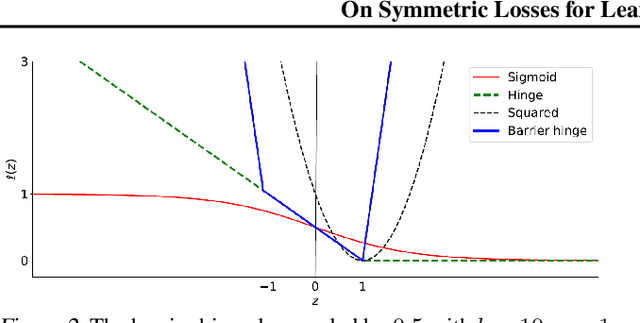
This paper aims to provide a better understanding of a symmetric loss. First, we show that using a symmetric loss is advantageous in the balanced error rate (BER) minimization and area under the receiver operating characteristic curve (AUC) maximization from corrupted labels. Second, we prove general theoretical properties of symmetric losses, including a classification-calibration condition, excess risk bound, conditional risk minimizer, and AUC-consistency condition. Third, since all nonnegative symmetric losses are non-convex, we propose a convex barrier hinge loss that benefits significantly from the symmetric condition, although it is not symmetric everywhere. Finally, we conduct experiments on BER and AUC optimization from corrupted labels to validate the relevance of the symmetric condition.