On Symmetric Losses for Learning from Corrupted Labels
Paper and Code
Jan 27, 2019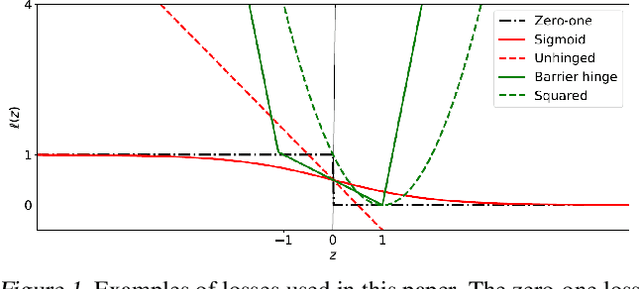

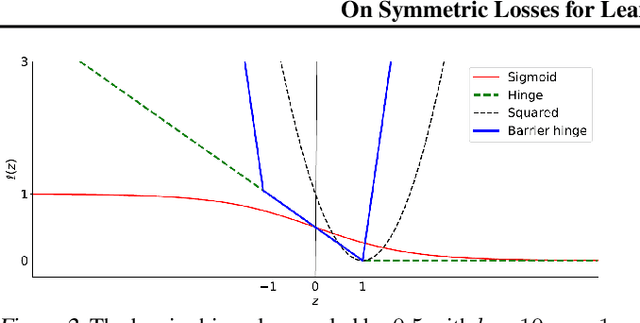

This paper aims to provide a better understanding of a symmetric loss. First, we show that using a symmetric loss is advantageous in the balanced error rate (BER) minimization and area under the receiver operating characteristic curve (AUC) maximization from corrupted labels. Second, we prove general theoretical properties of symmetric losses, including a classification-calibration condition, excess risk bound, conditional risk minimizer, and AUC-consistency condition. Third, since all nonnegative symmetric losses are non-convex, we propose a convex barrier hinge loss that benefits significantly from the symmetric condition, although it is not symmetric everywhere. Finally, we conduct experiments on BER and AUC optimization from corrupted labels to validate the relevance of the symmetric condition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge