Upper-Confidence-Bound Algorithms for Active Learning in Multi-Armed Bandits
Paper and Code
Jul 16, 2015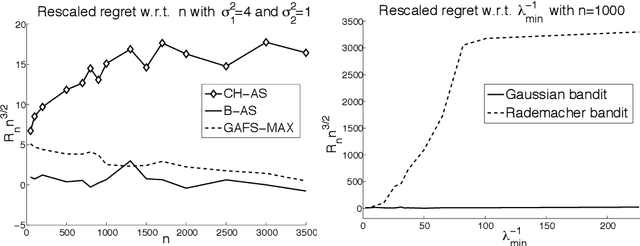
In this paper, we study the problem of estimating uniformly well the mean values of several distributions given a finite budget of samples. If the variance of the distributions were known, one could design an optimal sampling strategy by collecting a number of independent samples per distribution that is proportional to their variance. However, in the more realistic case where the distributions are not known in advance, one needs to design adaptive sampling strategies in order to select which distribution to sample from according to the previously observed samples. We describe two strategies based on pulling the distributions a number of times that is proportional to a high-probability upper-confidence-bound on their variance (built from previous observed samples) and report a finite-sample performance analysis on the excess estimation error compared to the optimal allocation. We show that the performance of these allocation strategies depends not only on the variances but also on the full shape of the distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge