Pareto Set Identification With Posterior Sampling
Paper and Code
Nov 07, 2024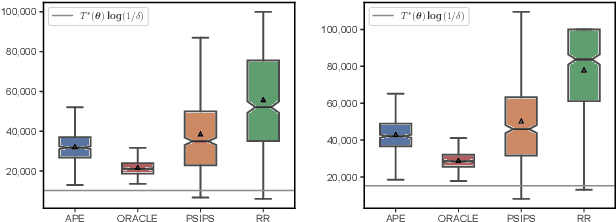

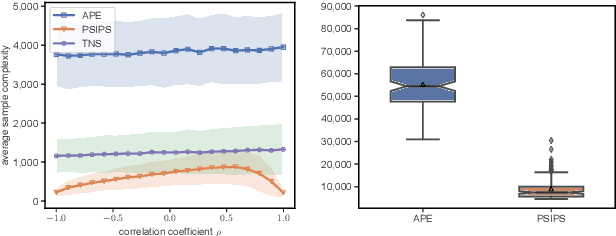

The problem of identifying the best answer among a collection of items having real-valued distribution is well-understood. Despite its practical relevance for many applications, fewer works have studied its extension when multiple and potentially conflicting metrics are available to assess an item's quality. Pareto set identification (PSI) aims to identify the set of answers whose means are not uniformly worse than another. This paper studies PSI in the transductive linear setting with potentially correlated objectives. Building on posterior sampling in both the stopping and the sampling rules, we propose the PSIPS algorithm that deals simultaneously with structure and correlation without paying the computational cost of existing oracle-based algorithms. Both from a frequentist and Bayesian perspective, PSIPS is asymptotically optimal. We demonstrate its good empirical performance in real-world and synthetic instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge