Optimal Posterior Sampling for Policy Identification in Tabular Markov Decision Processes

We study the $(\varepsilon, δ)$-PAC policy identification problem in finite-horizon episodic Markov Decision Processes. Existing approaches provide finite-time guarantees for approximate settings ($\varepsilon>0$) but suffer from high computational cost, rendering them hard to implement, and also suffer from suboptimal dependence on $\log(1/δ)$. We propose a randomized and computationally efficient algorithm for best policy identification that combines posterior sampling with an online learning algorithm to guide exploration in the MDP. Our method achieves asymptotic optimality in sample complexity, also in terms of posterior contraction rate, and runs in $O(S^2AH)$ per episode, matching standard model-based approaches. Unlike prior algorithms such as MOCA and PEDEL, our guarantees remain meaningful in the asymptotic regime and avoid sub-optimal polynomial dependence on $\log(1/δ)$. Our results provide both theoretical insights and practical tools for efficient policy identification in tabular MDPs.

Constrained Pareto Set Identification with Bandit Feedback

In this paper, we address the problem of identifying the Pareto Set under feasibility constraints in a multivariate bandit setting. Specifically, given a $K$-armed bandit with unknown means $\mu_1, \dots, \mu_K \in \mathbb{R}^d$, the goal is to identify the set of arms whose mean is not uniformly worse than that of another arm (i.e., not smaller for all objectives), while satisfying some known set of linear constraints, expressing, for example, some minimal performance on each objective. Our focus lies in fixed-confidence identification, for which we introduce an algorithm that significantly outperforms racing-like algorithms and the intuitive two-stage approach that first identifies feasible arms and then their Pareto Set. We further prove an information-theoretic lower bound on the sample complexity of any algorithm for constrained Pareto Set identification, showing that the sample complexity of our approach is near-optimal. Our theoretical results are supported by an extensive empirical evaluation on a series of benchmarks.

Pareto Set Identification With Posterior Sampling

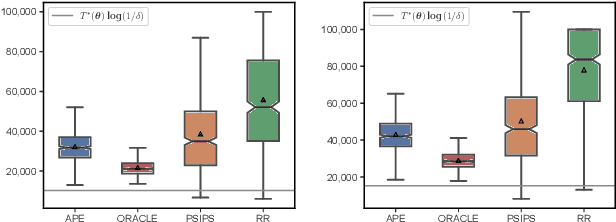
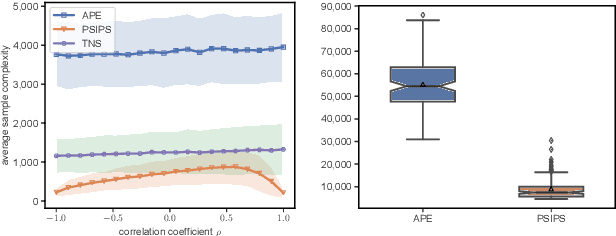
The problem of identifying the best answer among a collection of items having real-valued distribution is well-understood. Despite its practical relevance for many applications, fewer works have studied its extension when multiple and potentially conflicting metrics are available to assess an item's quality. Pareto set identification (PSI) aims to identify the set of answers whose means are not uniformly worse than another. This paper studies PSI in the transductive linear setting with potentially correlated objectives. Building on posterior sampling in both the stopping and the sampling rules, we propose the PSIPS algorithm that deals simultaneously with structure and correlation without paying the computational cost of existing oracle-based algorithms. Both from a frequentist and Bayesian perspective, PSIPS is asymptotically optimal. We demonstrate its good empirical performance in real-world and synthetic instances.

Bandit Pareto Set Identification: the Fixed Budget Setting

We study a multi-objective pure exploration problem in a multi-armed bandit model. Each arm is associated to an unknown multi-variate distribution and the goal is to identify the distributions whose mean is not uniformly worse than that of another distribution: the Pareto optimal set. We propose and analyze the first algorithms for the \emph{fixed budget} Pareto Set Identification task. We propose Empirical Gap Elimination, a family of algorithms combining a careful estimation of the ``hardness to classify'' each arm in or out of the Pareto set with a generic elimination scheme. We prove that two particular instances, EGE-SR and EGE-SH, have a probability of error that decays exponentially fast with the budget, with an exponent supported by an information theoretic lower-bound. We complement these findings with an empirical study using real-world and synthetic datasets, which showcase the good performance of our algorithms.

Adaptive Algorithms for Relaxed Pareto Set Identification

In this paper we revisit the fixed-confidence identification of the Pareto optimal set in a multi-objective multi-armed bandit model. As the sample complexity to identify the exact Pareto set can be very large, a relaxation allowing to output some additional near-optimal arms has been studied. In this work we also tackle alternative relaxations that allow instead to identify a relevant subset of the Pareto set. Notably, we propose a single sampling strategy, called Adaptive Pareto Exploration, that can be used in conjunction with different stopping rules to take into account different relaxations of the Pareto Set Identification problem. We analyze the sample complexity of these different combinations, quantifying in particular the reduction in sample complexity that occurs when one seeks to identify at most $k$ Pareto optimal arms. We showcase the good practical performance of Adaptive Pareto Exploration on a real-world scenario, in which we adaptively explore several vaccination strategies against Covid-19 in order to find the optimal ones when multiple immunogenicity criteria are taken into account.