Learning Parametric Distributions from Samples and Preferences

Recent advances in language modeling have underscored the role of preference feedback in enhancing model performance. This paper investigates the conditions under which preference feedback improves parameter estimation in classes of continuous parametric distributions. In our framework, the learner observes pairs of samples from an unknown distribution along with their relative preferences depending on the same unknown parameter. We show that preference-based M-estimators achieve a better asymptotic variance than sample-only M-estimators, further improved by deterministic preferences. Leveraging the hard constraints revealed by deterministic preferences, we propose an estimator achieving an estimation error scaling of $\mathcal{O}(1/n)$ -- a significant improvement over the $\Theta(1/\sqrt{n})$ rate attainable with samples alone. Next, we establish a lower bound that matches this accelerated rate; up to dimension and problem-dependent constants. While the assumptions underpinning our analysis are restrictive, they are satisfied by notable cases such as Gaussian or Laplace distributions for preferences based on the log-probability reward.

Pareto Set Identification With Posterior Sampling

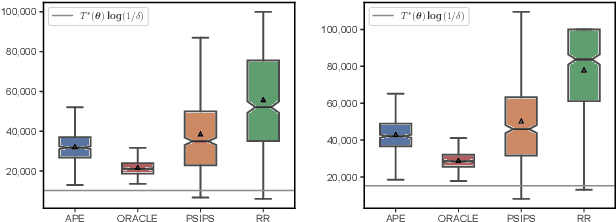
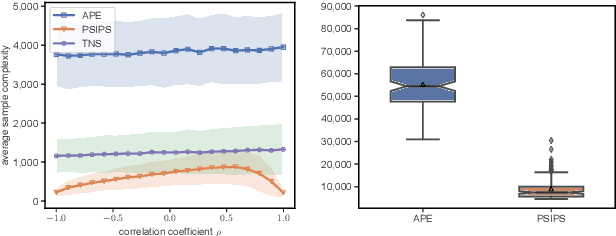
The problem of identifying the best answer among a collection of items having real-valued distribution is well-understood. Despite its practical relevance for many applications, fewer works have studied its extension when multiple and potentially conflicting metrics are available to assess an item's quality. Pareto set identification (PSI) aims to identify the set of answers whose means are not uniformly worse than another. This paper studies PSI in the transductive linear setting with potentially correlated objectives. Building on posterior sampling in both the stopping and the sampling rules, we propose the PSIPS algorithm that deals simultaneously with structure and correlation without paying the computational cost of existing oracle-based algorithms. Both from a frequentist and Bayesian perspective, PSIPS is asymptotically optimal. We demonstrate its good empirical performance in real-world and synthetic instances.

Best-Arm Identification in Unimodal Bandits

We study the fixed-confidence best-arm identification problem in unimodal bandits, in which the means of the arms increase with the index of the arm up to their maximum, then decrease. We derive two lower bounds on the stopping time of any algorithm. The instance-dependent lower bound suggests that due to the unimodal structure, only three arms contribute to the leading confidence-dependent cost. However, a worst-case lower bound shows that a linear dependence on the number of arms is unavoidable in the confidence-independent cost. We propose modifications of Track-and-Stop and a Top Two algorithm that leverage the unimodal structure. Both versions of Track-and-Stop are asymptotically optimal for one-parameter exponential families. The Top Two algorithm is asymptotically near-optimal for Gaussian distributions and we prove a non-asymptotic guarantee matching the worse-case lower bound. The algorithms can be implemented efficiently and we demonstrate their competitive empirical performance.

Differentially Private Best-Arm Identification

Best Arm Identification (BAI) problems are progressively used for data-sensitive applications, such as designing adaptive clinical trials, tuning hyper-parameters, and conducting user studies. Motivated by the data privacy concerns invoked by these applications, we study the problem of BAI with fixed confidence in both the local and central models, i.e. $\epsilon$-local and $\epsilon$-global Differential Privacy (DP). First, to quantify the cost of privacy, we derive lower bounds on the sample complexity of any $\delta$-correct BAI algorithm satisfying $\epsilon$-global DP or $\epsilon$-local DP. Our lower bounds suggest the existence of two privacy regimes. In the high-privacy regime, the hardness depends on a coupled effect of privacy and novel information-theoretic quantities involving the Total Variation. In the low-privacy regime, the lower bounds reduce to the non-private lower bounds. We propose $\epsilon$-local DP and $\epsilon$-global DP variants of a Top Two algorithm, namely CTB-TT and AdaP-TT*, respectively. For $\epsilon$-local DP, CTB-TT is asymptotically optimal by plugging in a private estimator of the means based on Randomised Response. For $\epsilon$-global DP, our private estimator of the mean runs in arm-dependent adaptive episodes and adds Laplace noise to ensure a good privacy-utility trade-off. By adapting the transportation costs, the expected sample complexity of AdaP-TT* reaches the asymptotic lower bound up to multiplicative constants.

An Anytime Algorithm for Good Arm Identification

In good arm identification (GAI), the goal is to identify one arm whose average performance exceeds a given threshold, referred to as good arm, if it exists. Few works have studied GAI in the fixed-budget setting, when the sampling budget is fixed beforehand, or the anytime setting, when a recommendation can be asked at any time. We propose APGAI, an anytime and parameter-free sampling rule for GAI in stochastic bandits. APGAI can be straightforwardly used in fixed-confidence and fixed-budget settings. First, we derive upper bounds on its probability of error at any time. They show that adaptive strategies are more efficient in detecting the absence of good arms than uniform sampling. Second, when APGAI is combined with a stopping rule, we prove upper bounds on the expected sampling complexity, holding at any confidence level. Finally, we show good empirical performance of APGAI on synthetic and real-world data. Our work offers an extensive overview of the GAI problem in all settings.

On the Complexity of Differentially Private Best-Arm Identification with Fixed Confidence

Best Arm Identification (BAI) problems are progressively used for data-sensitive applications, such as designing adaptive clinical trials, tuning hyper-parameters, and conducting user studies to name a few. Motivated by the data privacy concerns invoked by these applications, we study the problem of BAI with fixed confidence under $\epsilon$-global Differential Privacy (DP). First, to quantify the cost of privacy, we derive a lower bound on the sample complexity of any $\delta$-correct BAI algorithm satisfying $\epsilon$-global DP. Our lower bound suggests the existence of two privacy regimes depending on the privacy budget $\epsilon$. In the high-privacy regime (small $\epsilon$), the hardness depends on a coupled effect of privacy and a novel information-theoretic quantity, called the Total Variation Characteristic Time. In the low-privacy regime (large $\epsilon$), the sample complexity lower bound reduces to the classical non-private lower bound. Second, we propose AdaP-TT, an $\epsilon$-global DP variant of the Top Two algorithm. AdaP-TT runs in arm-dependent adaptive episodes and adds Laplace noise to ensure a good privacy-utility trade-off. We derive an asymptotic upper bound on the sample complexity of AdaP-TT that matches with the lower bound up to multiplicative constants in the high-privacy regime. Finally, we provide an experimental analysis of AdaP-TT that validates our theoretical results.

An $\varepsilon$-Best-Arm Identification Algorithm for Fixed-Confidence and Beyond

We propose EB-TC$\varepsilon$, a novel sampling rule for $\varepsilon$-best arm identification in stochastic bandits. It is the first instance of Top Two algorithm analyzed for approximate best arm identification. EB-TC$\varepsilon$ is an *anytime* sampling rule that can therefore be employed without modification for fixed confidence or fixed budget identification (without prior knowledge of the budget). We provide three types of theoretical guarantees for EB-TC$\varepsilon$. First, we prove bounds on its expected sample complexity in the fixed confidence setting, notably showing its asymptotic optimality in combination with an adaptive tuning of its exploration parameter. We complement these findings with upper bounds on its probability of error at any time and for any error parameter, which further yield upper bounds on its simple regret at any time. Finally, we show through numerical simulations that EB-TC$\varepsilon$ performs favorably compared to existing algorithms, in different settings.

Non-Asymptotic Analysis of a UCB-based Top Two Algorithm

A Top Two sampling rule for bandit identification is a method which selects the next arm to sample from among two candidate arms, a leader and a challenger. Due to their simplicity and good empirical performance, they have received increased attention in recent years. For fixed-confidence best arm identification, theoretical guarantees for Top Two methods have only been obtained in the asymptotic regime, when the error level vanishes. We derive the first non-asymptotic upper bound on the expected sample complexity of a Top Two algorithm holding for any error level. Our analysis highlights sufficient properties for a regret minimization algorithm to be used as leader. They are satisfied by the UCB algorithm and our proposed UCB-based Top Two algorithm enjoys simultaneously non-asymptotic guarantees and competitive empirical performance.

Dealing with Unknown Variances in Best-Arm Identification

The problem of identifying the best arm among a collection of items having Gaussian rewards distribution is well understood when the variances are known. Despite its practical relevance for many applications, few works studied it for unknown variances. In this paper we introduce and analyze two approaches to deal with unknown variances, either by plugging in the empirical variance or by adapting the transportation costs. In order to calibrate our two stopping rules, we derive new time-uniform concentration inequalities, which are of independent interest. Then, we illustrate the theoretical and empirical performances of our two sampling rule wrappers on Track-and-Stop and on a Top Two algorithm. Moreover, by quantifying the impact on the sample complexity of not knowing the variances, we reveal that it is rather small.

Top Two Algorithms Revisited

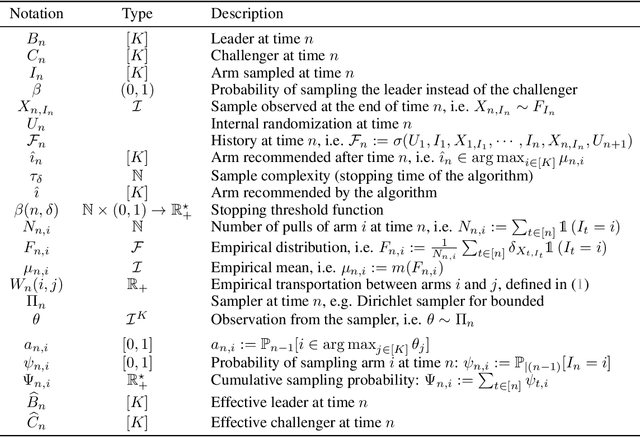
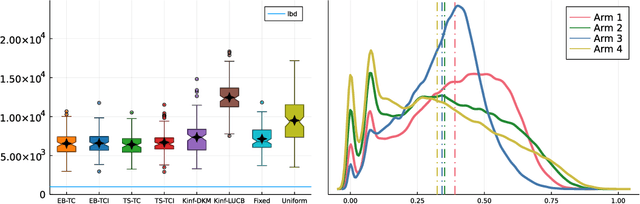
Top Two algorithms arose as an adaptation of Thompson sampling to best arm identification in multi-armed bandit models (Russo, 2016), for parametric families of arms. They select the next arm to sample from by randomizing among two candidate arms, a leader and a challenger. Despite their good empirical performance, theoretical guarantees for fixed-confidence best arm identification have only been obtained when the arms are Gaussian with known variances. In this paper, we provide a general analysis of Top Two methods, which identifies desirable properties of the leader, the challenger, and the (possibly non-parametric) distributions of the arms. As a result, we obtain theoretically supported Top Two algorithms for best arm identification with bounded distributions. Our proof method demonstrates in particular that the sampling step used to select the leader inherited from Thompson sampling can be replaced by other choices, like selecting the empirical best arm.