Top Two Algorithms Revisited
Paper and Code
Jun 13, 2022

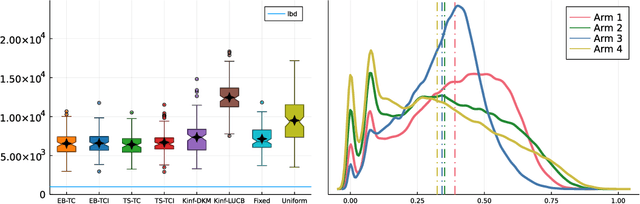
Top Two algorithms arose as an adaptation of Thompson sampling to best arm identification in multi-armed bandit models (Russo, 2016), for parametric families of arms. They select the next arm to sample from by randomizing among two candidate arms, a leader and a challenger. Despite their good empirical performance, theoretical guarantees for fixed-confidence best arm identification have only been obtained when the arms are Gaussian with known variances. In this paper, we provide a general analysis of Top Two methods, which identifies desirable properties of the leader, the challenger, and the (possibly non-parametric) distributions of the arms. As a result, we obtain theoretically supported Top Two algorithms for best arm identification with bounded distributions. Our proof method demonstrates in particular that the sampling step used to select the leader inherited from Thompson sampling can be replaced by other choices, like selecting the empirical best arm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge