The Value of Reward Lookahead in Reinforcement Learning

In reinforcement learning (RL), agents sequentially interact with changing environments while aiming to maximize the obtained rewards. Usually, rewards are observed only after acting, and so the goal is to maximize the expected cumulative reward. Yet, in many practical settings, reward information is observed in advance -- prices are observed before performing transactions; nearby traffic information is partially known; and goals are oftentimes given to agents prior to the interaction. In this work, we aim to quantifiably analyze the value of such future reward information through the lens of competitive analysis. In particular, we measure the ratio between the value of standard RL agents and that of agents with partial future-reward lookahead. We characterize the worst-case reward distribution and derive exact ratios for the worst-case reward expectations. Surprisingly, the resulting ratios relate to known quantities in offline RL and reward-free exploration. We further provide tight bounds for the ratio given the worst-case dynamics. Our results cover the full spectrum between observing the immediate rewards before acting to observing all the rewards before the interaction starts.

A General Recipe for the Analysis of Randomized Multi-Armed Bandit Algorithms

In this paper we propose a general methodology to derive regret bounds for randomized multi-armed bandit algorithms. It consists in checking a set of sufficient conditions on the sampling probability of each arm and on the family of distributions to prove a logarithmic regret. As a direct application we revisit two famous bandit algorithms, Minimum Empirical Divergence (MED) and Thompson Sampling (TS), under various models for the distributions including single parameter exponential families, Gaussian distributions, bounded distributions, or distributions satisfying some conditions on their moments. In particular, we prove that MED is asymptotically optimal for all these models, but also provide a simple regret analysis of some TS algorithms for which the optimality is already known. We then further illustrate the interest of our approach, by analyzing a new Non-Parametric TS algorithm (h-NPTS), adapted to some families of unbounded reward distributions with a bounded h-moment. This model can for instance capture some non-parametric families of distributions whose variance is upper bounded by a known constant.

Towards an efficient and risk aware strategy for guiding farmers in identifying best crop management

Identification of best performing fertilizer practices among a set of contrasting practices with field trials is challenging as crop losses are costly for farmers. To identify best management practices, an ''intuitive strategy'' would be to set multi-year field trials with equal proportion of each practice to test. Our objective was to provide an identification strategy using a bandit algorithm that was better at minimizing farmers' losses occurring during the identification, compared with the ''intuitive strategy''. We used a modification of the Decision Support Systems for Agro-Technological Transfer (DSSAT) crop model to mimic field trial responses, with a case-study in Southern Mali. We compared fertilizer practices using a risk-aware measure, the Conditional Value-at-Risk (CVaR), and a novel agronomic metric, the Yield Excess (YE). YE accounts for both grain yield and agronomic nitrogen use efficiency. The bandit-algorithm performed better than the intuitive strategy: it increased, in most cases, farmers' protection against worst outcomes. This study is a methodological step which opens up new horizons for risk-aware ensemble identification of the performance of contrasting crop management practices in real conditions.

Top Two Algorithms Revisited

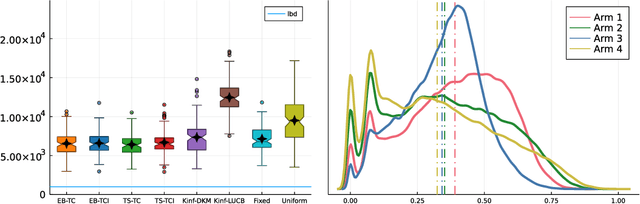
Top Two algorithms arose as an adaptation of Thompson sampling to best arm identification in multi-armed bandit models (Russo, 2016), for parametric families of arms. They select the next arm to sample from by randomizing among two candidate arms, a leader and a challenger. Despite their good empirical performance, theoretical guarantees for fixed-confidence best arm identification have only been obtained when the arms are Gaussian with known variances. In this paper, we provide a general analysis of Top Two methods, which identifies desirable properties of the leader, the challenger, and the (possibly non-parametric) distributions of the arms. As a result, we obtain theoretically supported Top Two algorithms for best arm identification with bounded distributions. Our proof method demonstrates in particular that the sampling step used to select the leader inherited from Thompson sampling can be replaced by other choices, like selecting the empirical best arm.

Efficient Algorithms for Extreme Bandits

In this paper, we contribute to the Extreme Bandit problem, a variant of Multi-Armed Bandits in which the learner seeks to collect the largest possible reward. We first study the concentration of the maximum of i.i.d random variables under mild assumptions on the tail of the rewards distributions. This analysis motivates the introduction of Quantile of Maxima (QoMax). The properties of QoMax are sufficient to build an Explore-Then-Commit (ETC) strategy, QoMax-ETC, achieving strong asymptotic guarantees despite its simplicity. We then propose and analyze a more adaptive, anytime algorithm, QoMax-SDA, which combines QoMax with a subsampling method recently introduced by Baudry et al. (2021). Both algorithms are more efficient than existing approaches in two aspects (1) they lead to better empirical performance (2) they enjoy a significant reduction of the memory and time complexities.

From Optimality to Robustness: Dirichlet Sampling Strategies in Stochastic Bandits

The stochastic multi-arm bandit problem has been extensively studied under standard assumptions on the arm's distribution (e.g bounded with known support, exponential family, etc). These assumptions are suitable for many real-world problems but sometimes they require knowledge (on tails for instance) that may not be precisely accessible to the practitioner, raising the question of the robustness of bandit algorithms to model misspecification. In this paper we study a generic Dirichlet Sampling (DS) algorithm, based on pairwise comparisons of empirical indices computed with re-sampling of the arms' observations and a data-dependent exploration bonus. We show that different variants of this strategy achieve provably optimal regret guarantees when the distributions are bounded and logarithmic regret for semi-bounded distributions with a mild quantile condition. We also show that a simple tuning achieve robustness with respect to a large class of unbounded distributions, at the cost of slightly worse than logarithmic asymptotic regret. We finally provide numerical experiments showing the merits of DS in a decision-making problem on synthetic agriculture data.

On Limited-Memory Subsampling Strategies for Bandits

There has been a recent surge of interest in nonparametric bandit algorithms based on subsampling. One drawback however of these approaches is the additional complexity required by random subsampling and the storage of the full history of rewards. Our first contribution is to show that a simple deterministic subsampling rule, proposed in the recent work of Baudry et al. (2020) under the name of ''last-block subsampling'', is asymptotically optimal in one-parameter exponential families. In addition, we prove that these guarantees also hold when limiting the algorithm memory to a polylogarithmic function of the time horizon. These findings open up new perspectives, in particular for non-stationary scenarios in which the arm distributions evolve over time. We propose a variant of the algorithm in which only the most recent observations are used for subsampling, achieving optimal regret guarantees under the assumption of a known number of abrupt changes. Extensive numerical simulations highlight the merits of this approach, particularly when the changes are not only affecting the means of the rewards.

Thompson Sampling for CVaR Bandits

Risk awareness is an important feature to formulate a variety of real world problems. In this paper we study a multi-arm bandit problem in which the quality of each arm is measured by the Conditional Value at Risk (CVaR) at some level {\alpha} of the reward distribution. While existing works in this setting mainly focus on Upper Confidence Bound algorithms, we introduce the first Thompson Sampling approaches for CVaR bandits. Building on a recent work by Riou and Honda (2020), we propose {\alpha}-NPTS for bounded rewards and {\alpha}-Multinomial-TS for multinomial distributions. We provide a novel lower bound on the CVaR regret which extends the concept of asymptotic optimality to CVaR bandits and prove that {\alpha}-Multinomial-TS is the first algorithm to achieve this lower bound. Finally, we demonstrate empirically the benefit of Thompson Sampling approaches over their UCB counterparts.

Sub-sampling for Efficient Non-Parametric Bandit Exploration

In this paper we propose the first multi-armed bandit algorithm based on re-sampling that achieves asymptotically optimal regret simultaneously for different families of arms (namely Bernoulli, Gaussian and Poisson distributions). Unlike Thompson Sampling which requires to specify a different prior to be optimal in each case, our proposal RB-SDA does not need any distribution-dependent tuning. RB-SDA belongs to the family of Sub-sampling Duelling Algorithms (SDA) which combines the sub-sampling idea first used by the BESA [1] and SSMC [2] algorithms with different sub-sampling schemes. In particular, RB-SDA uses Random Block sampling. We perform an experimental study assessing the flexibility and robustness of this promising novel approach for exploration in bandit models.