Mathematics of statistical sequential decision-making: concentration, risk-awareness and modelling in stochastic bandits, with applications to bariatric surgery

This thesis aims to study some of the mathematical challenges that arise in the analysis of statistical sequential decision-making algorithms for postoperative patients follow-up. Stochastic bandits (multiarmed, contextual) model the learning of a sequence of actions (policy) by an agent in an uncertain environment in order to maximise observed rewards. To learn optimal policies, bandit algorithms have to balance the exploitation of current knowledge and the exploration of uncertain actions. Such algorithms have largely been studied and deployed in industrial applications with large datasets, low-risk decisions and clear modelling assumptions, such as clickthrough rate maximisation in online advertising. By contrast, digital health recommendations call for a whole new paradigm of small samples, risk-averse agents and complex, nonparametric modelling. To this end, we developed new safe, anytime-valid concentration bounds, (Bregman, empirical Chernoff), introduced a new framework for risk-aware contextual bandits (with elicitable risk measures) and analysed a novel class of nonparametric bandit algorithms under weak assumptions (Dirichlet sampling). In addition to the theoretical guarantees, these results are supported by in-depth empirical evidence. Finally, as a first step towards personalised postoperative follow-up recommendations, we developed with medical doctors and surgeons an interpretable machine learning model to predict the long-term weight trajectories of patients after bariatric surgery.

Development and validation of an interpretable machine learning-based calculator for predicting 5-year weight trajectories after bariatric surgery: a multinational retrospective cohort SOPHIA study

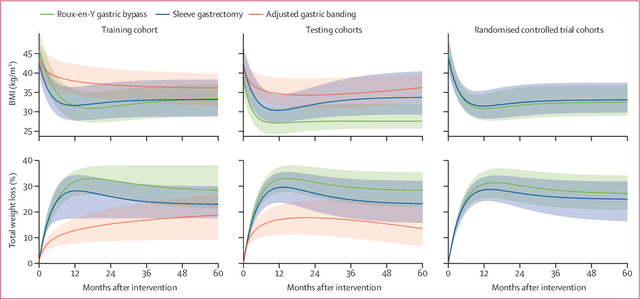
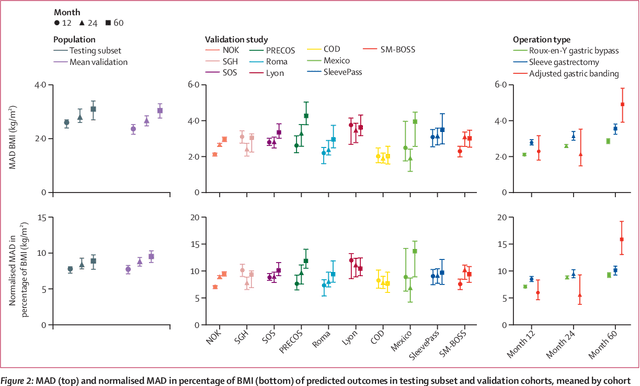
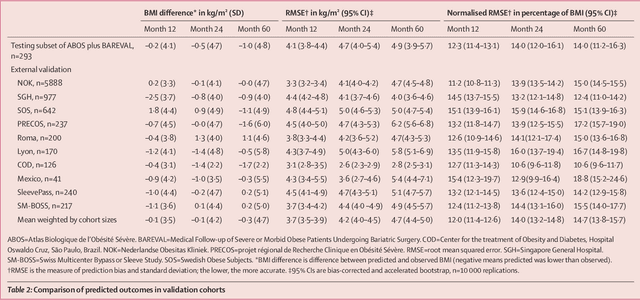
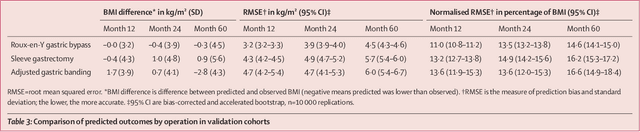
Background Weight loss trajectories after bariatric surgery vary widely between individuals, and predicting weight loss before the operation remains challenging. We aimed to develop a model using machine learning to provide individual preoperative prediction of 5-year weight loss trajectories after surgery. Methods In this multinational retrospective observational study we enrolled adult participants (aged $\ge$18 years) from ten prospective cohorts (including ABOS [NCT01129297], BAREVAL [NCT02310178], the Swedish Obese Subjects study, and a large cohort from the Dutch Obesity Clinic [Nederlandse Obesitas Kliniek]) and two randomised trials (SleevePass [NCT00793143] and SM-BOSS [NCT00356213]) in Europe, the Americas, and Asia, with a 5 year followup after Roux-en-Y gastric bypass, sleeve gastrectomy, or gastric band. Patients with a previous history of bariatric surgery or large delays between scheduled and actual visits were excluded. The training cohort comprised patients from two centres in France (ABOS and BAREVAL). The primary outcome was BMI at 5 years. A model was developed using least absolute shrinkage and selection operator to select variables and the classification and regression trees algorithm to build interpretable regression trees. The performances of the model were assessed through the median absolute deviation (MAD) and root mean squared error (RMSE) of BMI. Findings10 231 patients from 12 centres in ten countries were included in the analysis, corresponding to 30 602 patient-years. Among participants in all 12 cohorts, 7701 (75$\bullet$3%) were female, 2530 (24$\bullet$7%) were male. Among 434 baseline attributes available in the training cohort, seven variables were selected: height, weight, intervention type, age, diabetes status, diabetes duration, and smoking status. At 5 years, across external testing cohorts the overall mean MAD BMI was 2$\bullet$8 kg/m${}^2$ (95% CI 2$\bullet$6-3$\bullet$0) and mean RMSE BMI was 4$\bullet$7 kg/m${}^2$ (4$\bullet$4-5$\bullet$0), and the mean difference between predicted and observed BMI was-0$\bullet$3 kg/m${}^2$ (SD 4$\bullet$7). This model is incorporated in an easy to use and interpretable web-based prediction tool to help inform clinical decision before surgery. InterpretationWe developed a machine learning-based model, which is internationally validated, for predicting individual 5-year weight loss trajectories after three common bariatric interventions.

Risk-aware linear bandits with convex loss

In decision-making problems such as the multi-armed bandit, an agent learns sequentially by optimizing a certain feedback. While the mean reward criterion has been extensively studied, other measures that reflect an aversion to adverse outcomes, such as mean-variance or conditional value-at-risk (CVaR), can be of interest for critical applications (healthcare, agriculture). Algorithms have been proposed for such risk-aware measures under bandit feedback without contextual information. In this work, we study contextual bandits where such risk measures can be elicited as linear functions of the contexts through the minimization of a convex loss. A typical example that fits within this framework is the expectile measure, which is obtained as the solution of an asymmetric least-square problem. Using the method of mixtures for supermartingales, we derive confidence sequences for the estimation of such risk measures. We then propose an optimistic UCB algorithm to learn optimal risk-aware actions, with regret guarantees similar to those of generalized linear bandits. This approach requires solving a convex problem at each round of the algorithm, which we can relax by allowing only approximated solution obtained by online gradient descent, at the cost of slightly higher regret. We conclude by evaluating the resulting algorithms on numerical experiments.

Bregman Deviations of Generic Exponential Families

We revisit the method of mixture technique, also known as the Laplace method, to study the concentration phenomenon in generic exponential families. Combining the properties of Bregman divergence associated with log-partition function of the family with the method of mixtures for super-martingales, we establish a generic bound controlling the Bregman divergence between the parameter of the family and a finite sample estimate of the parameter. Our bound is time-uniform and makes appear a quantity extending the classical \textit{information gain} to exponential families, which we call the \textit{Bregman information gain}. For the practitioner, we instantiate this novel bound to several classical families, e.g., Gaussian, Bernoulli, Exponential and Chi-square yielding explicit forms of the confidence sets and the Bregman information gain. We further numerically compare the resulting confidence bounds to state-of-the-art alternatives for time-uniform concentration and show that this novel method yields competitive results. Finally, we highlight how our results can be applied in a linear contextual multi-armed bandit problem.

From Optimality to Robustness: Dirichlet Sampling Strategies in Stochastic Bandits

The stochastic multi-arm bandit problem has been extensively studied under standard assumptions on the arm's distribution (e.g bounded with known support, exponential family, etc). These assumptions are suitable for many real-world problems but sometimes they require knowledge (on tails for instance) that may not be precisely accessible to the practitioner, raising the question of the robustness of bandit algorithms to model misspecification. In this paper we study a generic Dirichlet Sampling (DS) algorithm, based on pairwise comparisons of empirical indices computed with re-sampling of the arms' observations and a data-dependent exploration bonus. We show that different variants of this strategy achieve provably optimal regret guarantees when the distributions are bounded and logarithmic regret for semi-bounded distributions with a mild quantile condition. We also show that a simple tuning achieve robustness with respect to a large class of unbounded distributions, at the cost of slightly worse than logarithmic asymptotic regret. We finally provide numerical experiments showing the merits of DS in a decision-making problem on synthetic agriculture data.