Best-Arm Identification in Unimodal Bandits

We study the fixed-confidence best-arm identification problem in unimodal bandits, in which the means of the arms increase with the index of the arm up to their maximum, then decrease. We derive two lower bounds on the stopping time of any algorithm. The instance-dependent lower bound suggests that due to the unimodal structure, only three arms contribute to the leading confidence-dependent cost. However, a worst-case lower bound shows that a linear dependence on the number of arms is unavoidable in the confidence-independent cost. We propose modifications of Track-and-Stop and a Top Two algorithm that leverage the unimodal structure. Both versions of Track-and-Stop are asymptotically optimal for one-parameter exponential families. The Top Two algorithm is asymptotically near-optimal for Gaussian distributions and we prove a non-asymptotic guarantee matching the worse-case lower bound. The algorithms can be implemented efficiently and we demonstrate their competitive empirical performance.

Truncating Trajectories in Monte Carlo Policy Evaluation: an Adaptive Approach

Policy evaluation via Monte Carlo (MC) simulation is at the core of many MC Reinforcement Learning (RL) algorithms (e.g., policy gradient methods). In this context, the designer of the learning system specifies an interaction budget that the agent usually spends by collecting trajectories of fixed length within a simulator. However, is this data collection strategy the best option? To answer this question, in this paper, we propose as a quality index a surrogate of the mean squared error of a return estimator that uses trajectories of different lengths, i.e., \emph{truncated}. Specifically, this surrogate shows the sub-optimality of the fixed-length trajectory schedule. Furthermore, it suggests that adaptive data collection strategies that spend the available budget sequentially can allocate a larger portion of transitions in timesteps in which more accurate sampling is required to reduce the error of the final estimate. Building on these findings, we present an adaptive algorithm called Robust and Iterative Data collection strategy Optimization (RIDO). The main intuition behind RIDO is to split the available interaction budget into mini-batches. At each round, the agent determines the most convenient schedule of trajectories that minimizes an empirical and robust version of the surrogate of the estimator's error. After discussing the theoretical properties of our method, we conclude by assessing its performance across multiple domains. Our results show that RIDO can adapt its trajectory schedule toward timesteps where more sampling is required to increase the quality of the final estimation.

Optimal Multi-Fidelity Best-Arm Identification

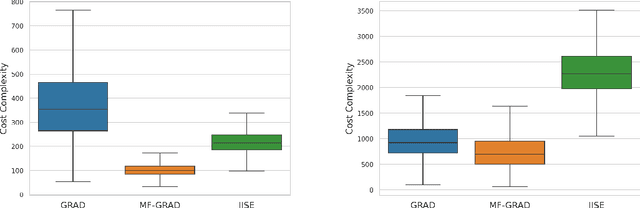
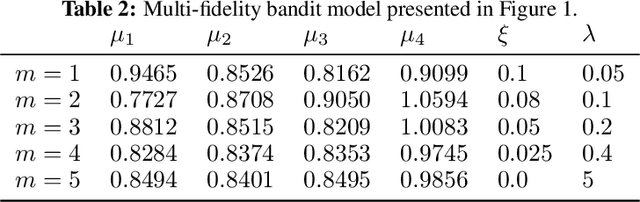
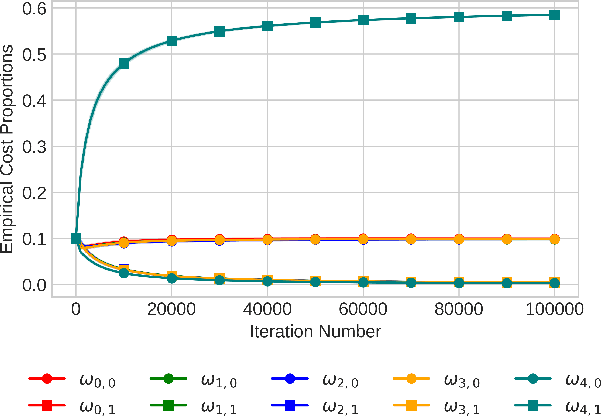
In bandit best-arm identification, an algorithm is tasked with finding the arm with highest mean reward with a specified accuracy as fast as possible. We study multi-fidelity best-arm identification, in which the algorithm can choose to sample an arm at a lower fidelity (less accurate mean estimate) for a lower cost. Several methods have been proposed for tackling this problem, but their optimality remain elusive, notably due to loose lower bounds on the total cost needed to identify the best arm. Our first contribution is a tight, instance-dependent lower bound on the cost complexity. The study of the optimization problem featured in the lower bound provides new insights to devise computationally efficient algorithms, and leads us to propose a gradient-based approach with asymptotically optimal cost complexity. We demonstrate the benefits of the new algorithm compared to existing methods in experiments. Our theoretical and empirical findings also shed light on an intriguing concept of optimal fidelity for each arm.

Inverse Reinforcement Learning with Sub-optimal Experts

Inverse Reinforcement Learning (IRL) techniques deal with the problem of deducing a reward function that explains the behavior of an expert agent who is assumed to act optimally in an underlying unknown task. In several problems of interest, however, it is possible to observe the behavior of multiple experts with different degree of optimality (e.g., racing drivers whose skills ranges from amateurs to professionals). For this reason, in this work, we extend the IRL formulation to problems where, in addition to demonstrations from the optimal agent, we can observe the behavior of multiple sub-optimal experts. Given this problem, we first study the theoretical properties of the class of reward functions that are compatible with a given set of experts, i.e., the feasible reward set. Our results show that the presence of multiple sub-optimal experts can significantly shrink the set of compatible rewards. Furthermore, we study the statistical complexity of estimating the feasible reward set with a generative model. To this end, we analyze a uniform sampling algorithm that results in being minimax optimal whenever the sub-optimal experts' performance level is sufficiently close to the one of the optimal agent.

Pure Exploration under Mediators' Feedback

Stochastic multi-armed bandits are a sequential-decision-making framework, where, at each interaction step, the learner selects an arm and observes a stochastic reward. Within the context of best-arm identification (BAI) problems, the goal of the agent lies in finding the optimal arm, i.e., the one with highest expected reward, as accurately and efficiently as possible. Nevertheless, the sequential interaction protocol of classical BAI problems, where the agent has complete control over the arm being pulled at each round, does not effectively model several decision-making problems of interest (e.g., off-policy learning, partially controllable environments, and human feedback). For this reason, in this work, we propose a novel strict generalization of the classical BAI problem that we refer to as best-arm identification under mediators' feedback (BAI-MF). More specifically, we consider the scenario in which the learner has access to a set of mediators, each of which selects the arms on the agent's behalf according to a stochastic and possibly unknown policy. The mediator, then, communicates back to the agent the pulled arm together with the observed reward. In this setting, the agent's goal lies in sequentially choosing which mediator to query to identify with high probability the optimal arm while minimizing the identification time, i.e., the sample complexity. To this end, we first derive and analyze a statistical lower bound on the sample complexity specific to our general mediator feedback scenario. Then, we propose a sequential decision-making strategy for discovering the best arm under the assumption that the mediators' policies are known to the learner. As our theory verifies, this algorithm matches the lower bound both almost surely and in expectation. Finally, we extend these results to cases where the mediators' policies are unknown to the learner obtaining comparable results.

Truncating Trajectories in Monte Carlo Reinforcement Learning

In Reinforcement Learning (RL), an agent acts in an unknown environment to maximize the expected cumulative discounted sum of an external reward signal, i.e., the expected return. In practice, in many tasks of interest, such as policy optimization, the agent usually spends its interaction budget by collecting episodes of fixed length within a simulator (i.e., Monte Carlo simulation). However, given the discounted nature of the RL objective, this data collection strategy might not be the best option. Indeed, the rewards taken in early simulation steps weigh exponentially more than future rewards. Taking a cue from this intuition, in this paper, we design an a-priori budget allocation strategy that leads to the collection of trajectories of different lengths, i.e., truncated. The proposed approach provably minimizes the width of the confidence intervals around the empirical estimates of the expected return of a policy. After discussing the theoretical properties of our method, we make use of our trajectory truncation mechanism to extend Policy Optimization via Importance Sampling (POIS, Metelli et al., 2018) algorithm. Finally, we conduct a numerical comparison between our algorithm and POIS: the results are consistent with our theory and show that an appropriate truncation of the trajectories can succeed in improving performance.

Optimizing Empty Container Repositioning and Fleet Deployment via Configurable Semi-POMDPs

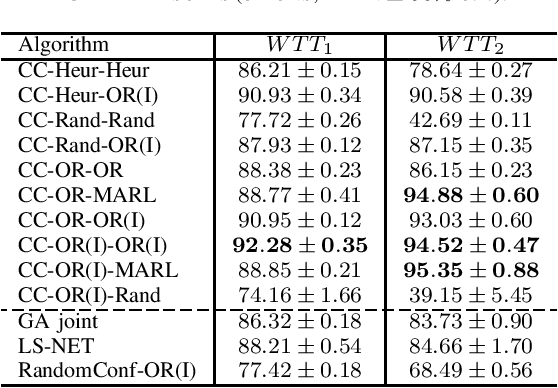
With the continuous growth of the global economy and markets, resource imbalance has risen to be one of the central issues in real logistic scenarios. In marine transportation, this trade imbalance leads to Empty Container Repositioning (ECR) problems. Once the freight has been delivered from an exporting country to an importing one, the laden will turn into empty containers that need to be repositioned to satisfy new goods requests in exporting countries. In such problems, the performance that any cooperative repositioning policy can achieve strictly depends on the routes that vessels will follow (i.e., fleet deployment). Historically, Operation Research (OR) approaches were proposed to jointly optimize the repositioning policy along with the fleet of vessels. However, the stochasticity of future supply and demand of containers, together with black-box and non-linear constraints that are present within the environment, make these approaches unsuitable for these scenarios. In this paper, we introduce a novel framework, Configurable Semi-POMDPs, to model this type of problems. Furthermore, we provide a two-stage learning algorithm, "Configure & Conquer" (CC), that first configures the environment by finding an approximation of the optimal fleet deployment strategy, and then "conquers" it by learning an ECR policy in this tuned environmental setting. We validate our approach in large and real-world instances of the problem. Our experiments highlight that CC avoids the pitfalls of OR methods and that it is successful at optimizing both the ECR policy and the fleet of vessels, leading to superior performance in world trade environments.

Meta-Reinforcement Learning by Tracking Task Non-stationarity

Many real-world domains are subject to a structured non-stationarity which affects the agent's goals and the environmental dynamics. Meta-reinforcement learning (RL) has been shown successful for training agents that quickly adapt to related tasks. However, most of the existing meta-RL algorithms for non-stationary domains either make strong assumptions on the task generation process or require sampling from it at training time. In this paper, we propose a novel algorithm (TRIO) that optimizes for the future by explicitly tracking the task evolution through time. At training time, TRIO learns a variational module to quickly identify latent parameters from experience samples. This module is learned jointly with an optimal exploration policy that takes task uncertainty into account. At test time, TRIO tracks the evolution of the latent parameters online, hence reducing the uncertainty over future tasks and obtaining fast adaptation through the meta-learned policy. Unlike most existing methods, TRIO does not assume Markovian task-evolution processes, it does not require information about the non-stationarity at training time, and it captures complex changes undergoing in the environment. We evaluate our algorithm on different simulated problems and show it outperforms competitive baselines.

Sequential Transfer in Reinforcement Learning with a Generative Model

We are interested in how to design reinforcement learning agents that provably reduce the sample complexity for learning new tasks by transferring knowledge from previously-solved ones. The availability of solutions to related problems poses a fundamental trade-off: whether to seek policies that are expected to achieve high (yet sub-optimal) performance in the new task immediately or whether to seek information to quickly identify an optimal solution, potentially at the cost of poor initial behavior. In this work, we focus on the second objective when the agent has access to a generative model of state-action pairs. First, given a set of solved tasks containing an approximation of the target one, we design an algorithm that quickly identifies an accurate solution by seeking the state-action pairs that are most informative for this purpose. We derive PAC bounds on its sample complexity which clearly demonstrate the benefits of using this kind of prior knowledge. Then, we show how to learn these approximate tasks sequentially by reducing our transfer setting to a hidden Markov model and employing spectral methods to recover its parameters. Finally, we empirically verify our theoretical findings in simple simulated domains.