Optimal Multi-Fidelity Best-Arm Identification
Paper and Code
Jun 05, 2024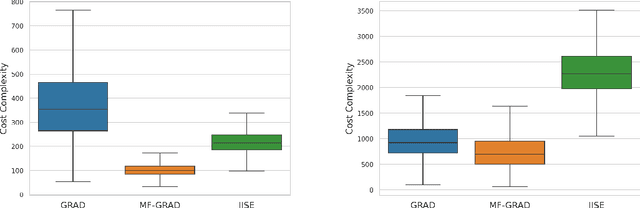

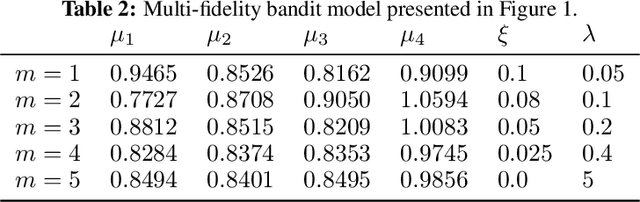
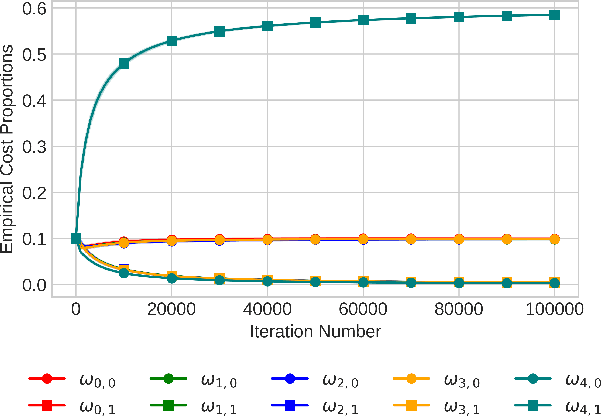
In bandit best-arm identification, an algorithm is tasked with finding the arm with highest mean reward with a specified accuracy as fast as possible. We study multi-fidelity best-arm identification, in which the algorithm can choose to sample an arm at a lower fidelity (less accurate mean estimate) for a lower cost. Several methods have been proposed for tackling this problem, but their optimality remain elusive, notably due to loose lower bounds on the total cost needed to identify the best arm. Our first contribution is a tight, instance-dependent lower bound on the cost complexity. The study of the optimization problem featured in the lower bound provides new insights to devise computationally efficient algorithms, and leads us to propose a gradient-based approach with asymptotically optimal cost complexity. We demonstrate the benefits of the new algorithm compared to existing methods in experiments. Our theoretical and empirical findings also shed light on an intriguing concept of optimal fidelity for each arm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge