Differentially Private Best-Arm Identification

Best Arm Identification (BAI) problems are progressively used for data-sensitive applications, such as designing adaptive clinical trials, tuning hyper-parameters, and conducting user studies. Motivated by the data privacy concerns invoked by these applications, we study the problem of BAI with fixed confidence in both the local and central models, i.e. $\epsilon$-local and $\epsilon$-global Differential Privacy (DP). First, to quantify the cost of privacy, we derive lower bounds on the sample complexity of any $\delta$-correct BAI algorithm satisfying $\epsilon$-global DP or $\epsilon$-local DP. Our lower bounds suggest the existence of two privacy regimes. In the high-privacy regime, the hardness depends on a coupled effect of privacy and novel information-theoretic quantities involving the Total Variation. In the low-privacy regime, the lower bounds reduce to the non-private lower bounds. We propose $\epsilon$-local DP and $\epsilon$-global DP variants of a Top Two algorithm, namely CTB-TT and AdaP-TT*, respectively. For $\epsilon$-local DP, CTB-TT is asymptotically optimal by plugging in a private estimator of the means based on Randomised Response. For $\epsilon$-global DP, our private estimator of the mean runs in arm-dependent adaptive episodes and adds Laplace noise to ensure a good privacy-utility trade-off. By adapting the transportation costs, the expected sample complexity of AdaP-TT* reaches the asymptotic lower bound up to multiplicative constants.

How Much Does Each Datapoint Leak Your Privacy? Quantifying the Per-datum Membership Leakage

We study the per-datum Membership Inference Attacks (MIAs), where an attacker aims to infer whether a fixed target datum has been included in the input dataset of an algorithm and thus, violates privacy. First, we define the membership leakage of a datum as the advantage of the optimal adversary targeting to identify it. Then, we quantify the per-datum membership leakage for the empirical mean, and show that it depends on the Mahalanobis distance between the target datum and the data-generating distribution. We further assess the effect of two privacy defences, i.e. adding Gaussian noise and sub-sampling. We quantify exactly how both of them decrease the per-datum membership leakage. Our analysis builds on a novel proof technique that combines an Edgeworth expansion of the likelihood ratio test and a Lindeberg-Feller central limit theorem. Our analysis connects the existing likelihood ratio and scalar product attacks, and also justifies different canary selection strategies used in the privacy auditing literature. Finally, our experiments demonstrate the impacts of the leakage score, the sub-sampling ratio and the noise scale on the per-datum membership leakage as indicated by the theory.

Conservative Exploration for Policy Optimization via Off-Policy Policy Evaluation

A precondition for the deployment of a Reinforcement Learning agent to a real-world system is to provide guarantees on the learning process. While a learning algorithm will eventually converge to a good policy, there are no guarantees on the performance of the exploratory policies. We study the problem of conservative exploration, where the learner must at least be able to guarantee its performance is at least as good as a baseline policy. We propose the first conservative provably efficient model-free algorithm for policy optimization in continuous finite-horizon problems. We leverage importance sampling techniques to counterfactually evaluate the conservative condition from the data self-generated by the algorithm. We derive a regret bound and show that (w.h.p.) the conservative constraint is never violated during learning. Finally, we leverage these insights to build a general schema for conservative exploration in DeepRL via off-policy policy evaluation techniques. We show empirically the effectiveness of our methods.

On the Complexity of Differentially Private Best-Arm Identification with Fixed Confidence

Best Arm Identification (BAI) problems are progressively used for data-sensitive applications, such as designing adaptive clinical trials, tuning hyper-parameters, and conducting user studies to name a few. Motivated by the data privacy concerns invoked by these applications, we study the problem of BAI with fixed confidence under $\epsilon$-global Differential Privacy (DP). First, to quantify the cost of privacy, we derive a lower bound on the sample complexity of any $\delta$-correct BAI algorithm satisfying $\epsilon$-global DP. Our lower bound suggests the existence of two privacy regimes depending on the privacy budget $\epsilon$. In the high-privacy regime (small $\epsilon$), the hardness depends on a coupled effect of privacy and a novel information-theoretic quantity, called the Total Variation Characteristic Time. In the low-privacy regime (large $\epsilon$), the sample complexity lower bound reduces to the classical non-private lower bound. Second, we propose AdaP-TT, an $\epsilon$-global DP variant of the Top Two algorithm. AdaP-TT runs in arm-dependent adaptive episodes and adds Laplace noise to ensure a good privacy-utility trade-off. We derive an asymptotic upper bound on the sample complexity of AdaP-TT that matches with the lower bound up to multiplicative constants in the high-privacy regime. Finally, we provide an experimental analysis of AdaP-TT that validates our theoretical results.

Interactive and Concentrated Differential Privacy for Bandits

Bandits play a crucial role in interactive learning schemes and modern recommender systems. However, these systems often rely on sensitive user data, making privacy a critical concern. This paper investigates privacy in bandits with a trusted centralized decision-maker through the lens of interactive Differential Privacy (DP). While bandits under pure $\epsilon$-global DP have been well-studied, we contribute to the understanding of bandits under zero Concentrated DP (zCDP). We provide minimax and problem-dependent lower bounds on regret for finite-armed and linear bandits, which quantify the cost of $\rho$-global zCDP in these settings. These lower bounds reveal two hardness regimes based on the privacy budget $\rho$ and suggest that $\rho$-global zCDP incurs less regret than pure $\epsilon$-global DP. We propose two $\rho$-global zCDP bandit algorithms, AdaC-UCB and AdaC-GOPE, for finite-armed and linear bandits respectively. Both algorithms use a common recipe of Gaussian mechanism and adaptive episodes. We analyze the regret of these algorithms to show that AdaC-UCB achieves the problem-dependent regret lower bound up to multiplicative constants, while AdaC-GOPE achieves the minimax regret lower bound up to poly-logarithmic factors. Finally, we provide experimental validation of our theoretical results under different settings.

When Privacy Meets Partial Information: A Refined Analysis of Differentially Private Bandits

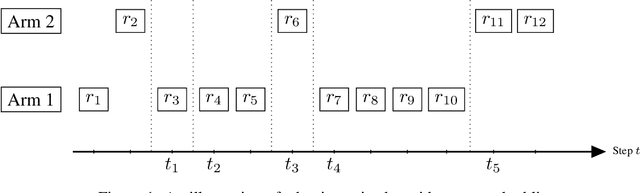
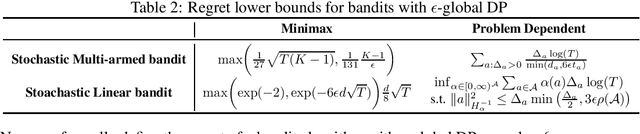
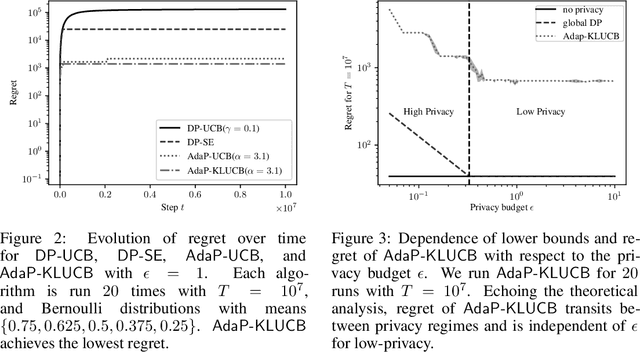
We study the problem of multi-armed bandits with $\epsilon$-global Differential Privacy (DP). First, we prove the minimax and problem-dependent regret lower bounds for stochastic and linear bandits that quantify the hardness of bandits with $\epsilon$-global DP. These bounds suggest the existence of two hardness regimes depending on the privacy budget $\epsilon$. In the high-privacy regime (small $\epsilon$), the hardness depends on a coupled effect of privacy and partial information about the reward distributions. In the low-privacy regime (large $\epsilon$), bandits with $\epsilon$-global DP are not harder than the bandits without privacy. For stochastic bandits, we further propose a generic framework to design a near-optimal $\epsilon$ global DP extension of an index-based optimistic bandit algorithm. The framework consists of three ingredients: the Laplace mechanism, arm-dependent adaptive episodes, and usage of only the rewards collected in the last episode for computing private statistics. Specifically, we instantiate $\epsilon$-global DP extensions of UCB and KL-UCB algorithms, namely AdaP-UCB and AdaP-KLUCB. AdaP-KLUCB is the first algorithm that both satisfies $\epsilon$-global DP and yields a regret upper bound that matches the problem-dependent lower bound up to multiplicative constants.

Conservative Optimistic Policy Optimization via Multiple Importance Sampling

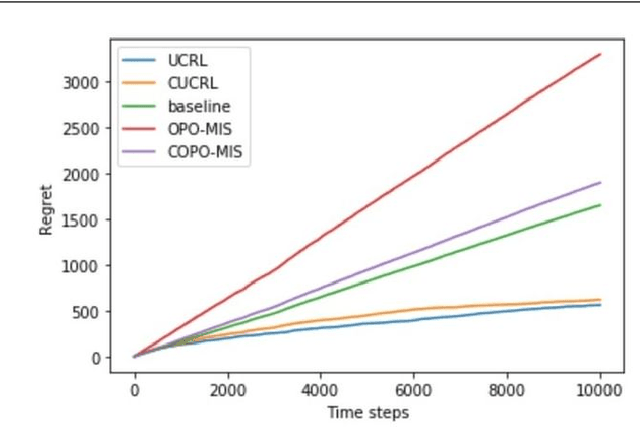
Reinforcement Learning (RL) has been able to solve hard problems such as playing Atari games or solving the game of Go, with a unified approach. Yet modern deep RL approaches are still not widely used in real-world applications. One reason could be the lack of guarantees on the performance of the intermediate executed policies, compared to an existing (already working) baseline policy. In this paper, we propose an online model-free algorithm that solves conservative exploration in the policy optimization problem. We show that the regret of the proposed approach is bounded by $\tilde{\mathcal{O}}(\sqrt{T})$ for both discrete and continuous parameter spaces.