Conservative Exploration for Policy Optimization via Off-Policy Policy Evaluation

A precondition for the deployment of a Reinforcement Learning agent to a real-world system is to provide guarantees on the learning process. While a learning algorithm will eventually converge to a good policy, there are no guarantees on the performance of the exploratory policies. We study the problem of conservative exploration, where the learner must at least be able to guarantee its performance is at least as good as a baseline policy. We propose the first conservative provably efficient model-free algorithm for policy optimization in continuous finite-horizon problems. We leverage importance sampling techniques to counterfactually evaluate the conservative condition from the data self-generated by the algorithm. We derive a regret bound and show that (w.h.p.) the conservative constraint is never violated during learning. Finally, we leverage these insights to build a general schema for conservative exploration in DeepRL via off-policy policy evaluation techniques. We show empirically the effectiveness of our methods.

SALSA PICANTE: a machine learning attack on LWE with binary secrets

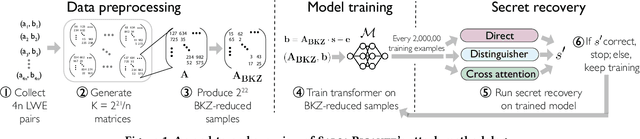
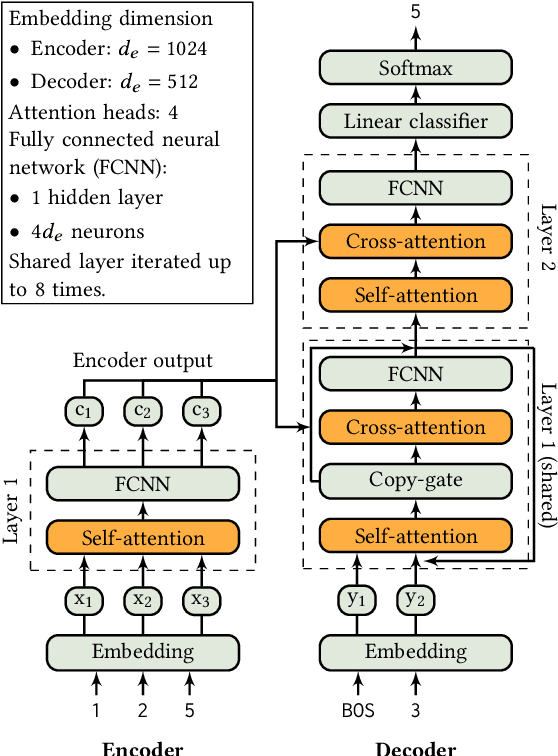
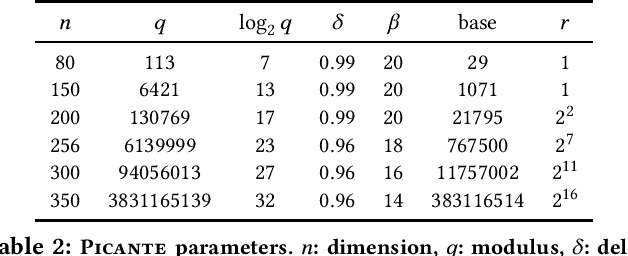
The Learning With Errors (LWE) problem is one of the major hard problems in post-quantum cryptography. For example, 1) the only Key Exchange Mechanism KEM standardized by NIST [14] is based on LWE; and 2) current publicly available Homomorphic Encryption (HE) libraries are based on LWE. NIST KEM schemes use random secrets, but homomorphic encryption schemes use binary or ternary secrets, for efficiency reasons. In particular, sparse binary secrets have been proposed, but not standardized [2], for HE. Prior work SALSA [49] demonstrated a new machine learning attack on sparse binary secrets for the LWE problem in small dimensions (up to n = 128) and low Hamming weights (up to h = 4). However, this attack assumed access to millions of LWE samples, and was not scaled to higher Hamming weights or dimensions. Our attack, PICANTE, reduces the number of samples required to just m = 4n samples. Moreover, it can recover secrets with much larger dimensions (up to 350) and Hamming weights (roughly n/10, or h = 33 for n = 300). To achieve this, we introduce a preprocessing step which allows us to generate the training data from a linear number of samples and changes the distribution of the training data to improve transformer training. We also improve the distinguisher/secret recovery methods of SALSA and introduce a novel cross-attention recovery mechanism which allows us to read-off the secret directly from the trained models.

Top $K$ Ranking for Multi-Armed Bandit with Noisy Evaluations

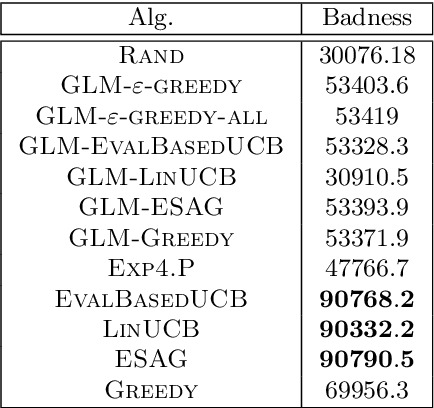
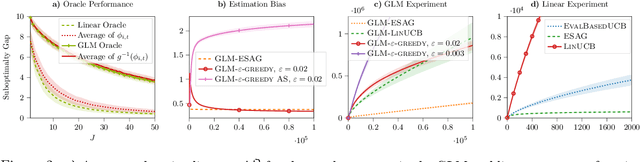
We consider a multi-armed bandit setting where, at the beginning of each round, the learner receives noisy independent, and possibly biased, \emph{evaluations} of the true reward of each arm and it selects $K$ arms with the objective of accumulating as much reward as possible over $T$ rounds. Under the assumption that at each round the true reward of each arm is drawn from a fixed distribution, we derive different algorithmic approaches and theoretical guarantees depending on how the evaluations are generated. First, we show a $\widetilde{O}(T^{2/3})$ regret in the general case when the observation functions are a genearalized linear function of the true rewards. On the other hand, we show that an improved $\widetilde{O}(\sqrt{T})$ regret can be derived when the observation functions are noisy linear functions of the true rewards. Finally, we report an empirical validation that confirms our theoretical findings, provides a thorough comparison to alternative approaches, and further supports the interest of this setting in practice.

Privacy Amplification via Shuffling for Linear Contextual Bandits

Contextual bandit algorithms are widely used in domains where it is desirable to provide a personalized service by leveraging contextual information, that may contain sensitive information that needs to be protected. Inspired by this scenario, we study the contextual linear bandit problem with differential privacy (DP) constraints. While the literature has focused on either centralized (joint DP) or local (local DP) privacy, we consider the shuffle model of privacy and we show that is possible to achieve a privacy/utility trade-off between JDP and LDP. By leveraging shuffling from privacy and batching from bandits, we present an algorithm with regret bound $\widetilde{\mathcal{O}}(T^{2/3}/\varepsilon^{1/3})$, while guaranteeing both central (joint) and local privacy. Our result shows that it is possible to obtain a trade-off between JDP and LDP by leveraging the shuffle model while preserving local privacy.

Differentially Private Exploration in Reinforcement Learning with Linear Representation

This paper studies privacy-preserving exploration in Markov Decision Processes (MDPs) with linear representation. We first consider the setting of linear-mixture MDPs (Ayoub et al., 2020) (a.k.a.\ model-based setting) and provide an unified framework for analyzing joint and local differential private (DP) exploration. Through this framework, we prove a $\widetilde{O}(K^{3/4}/\sqrt{\epsilon})$ regret bound for $(\epsilon,\delta)$-local DP exploration and a $\widetilde{O}(\sqrt{K/\epsilon})$ regret bound for $(\epsilon,\delta)$-joint DP. We further study privacy-preserving exploration in linear MDPs (Jin et al., 2020) (a.k.a.\ model-free setting) where we provide a $\widetilde{O}\left(K^{\frac{3}{5}}/\epsilon^{\frac{2}{5}}\right)$ regret bound for $(\epsilon,\delta)$-joint DP, with a novel algorithm based on low-switching. Finally, we provide insights into the issues of designing local DP algorithms in this model-free setting.

A Unified Framework for Conservative Exploration

We study bandits and reinforcement learning (RL) subject to a conservative constraint where the agent is asked to perform at least as well as a given baseline policy. This setting is particular relevant in real-world domains including digital marketing, healthcare, production, finance, etc. For multi-armed bandits, linear bandits and tabular RL, specialized algorithms and theoretical analyses were proposed in previous work. In this paper, we present a unified framework for conservative bandits and RL, in which our core technique is to calculate the necessary and sufficient budget obtained from running the baseline policy. For lower bounds, our framework gives a black-box reduction that turns a certain lower bound in the nonconservative setting into a new lower bound in the conservative setting. We strengthen the existing lower bound for conservative multi-armed bandits and obtain new lower bounds for conservative linear bandits, tabular RL and low-rank MDP. For upper bounds, our framework turns a certain nonconservative upper-confidence-bound (UCB) algorithm into a conservative algorithm with a simple analysis. For multi-armed bandits, linear bandits and tabular RL, our new upper bounds tighten or match existing ones with significantly simpler analyses. We also obtain a new upper bound for conservative low-rank MDP.

Homomorphically Encrypted Linear Contextual Bandit

Contextual bandit is a general framework for online learning in sequential decision-making problems that has found application in a large range of domains, including recommendation system, online advertising, clinical trials and many more. A critical aspect of bandit methods is that they require to observe the contexts -- i.e., individual or group-level data -- and the rewards in order to solve the sequential problem. The large deployment in industrial applications has increased interest in methods that preserve the privacy of the users. In this paper, we introduce a privacy-preserving bandit framework based on asymmetric encryption. The bandit algorithm only observes encrypted information (contexts and rewards) and has no ability to decrypt it. Leveraging homomorphic encryption, we show that despite the complexity of the setting, it is possible to learn over encrypted data. We introduce an algorithm that achieves a $\widetilde{O}(d\sqrt{T})$ regret bound in any linear contextual bandit problem, while keeping data encrypted.

Local Differentially Private Regret Minimization in Reinforcement Learning

Reinforcement learning algorithms are widely used in domains where it is desirable to provide a personalized service. In these domains it is common that user data contains sensitive information that needs to be protected from third parties. Motivated by this, we study privacy in the context of finite-horizon Markov Decision Processes (MDPs) by requiring information to be obfuscated on the user side. We formulate this notion of privacy for RL by leveraging the local differential privacy (LDP) framework. We present an optimistic algorithm that simultaneously satisfies LDP requirements, and achieves sublinear regret. We also establish a lower bound for regret minimization in finite-horizon MDPs with LDP guarantees. These results show that while LDP is appealing in practical applications, the setting is inherently more complex. In particular, our results demonstrate that the cost of privacy is multiplicative when compared to non-private settings.

Adversarial Attacks on Linear Contextual Bandits

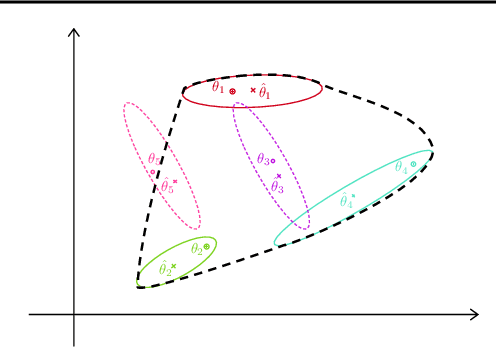
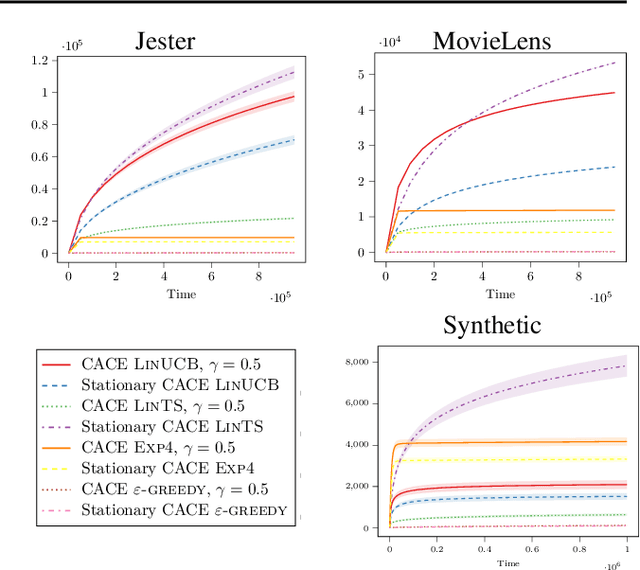
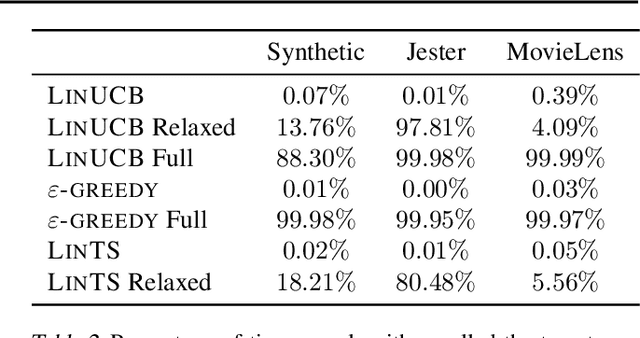
Contextual bandit algorithms are applied in a wide range of domains, from advertising to recommender systems, from clinical trials to education. In many of these domains, malicious agents may have incentives to attack the bandit algorithm to induce it to perform a desired behavior. For instance, an unscrupulous ad publisher may try to increase their own revenue at the expense of the advertisers; a seller may want to increase the exposure of their products, or thwart a competitor's advertising campaign. In this paper, we study several attack scenarios and show that a malicious agent can force a linear contextual bandit algorithm to pull any desired arm $T - o(T)$ times over a horizon of $T$ steps, while applying adversarial modifications to either rewards or contexts that only grow logarithmically as $O(\log T)$. We also investigate the case when a malicious agent is interested in affecting the behavior of the bandit algorithm in a single context (e.g., a specific user). We first provide sufficient conditions for the feasibility of the attack and we then propose an efficient algorithm to perform the attack. We validate our theoretical results on experiments performed on both synthetic and real-world datasets.

Improved Algorithms for Conservative Exploration in Bandits

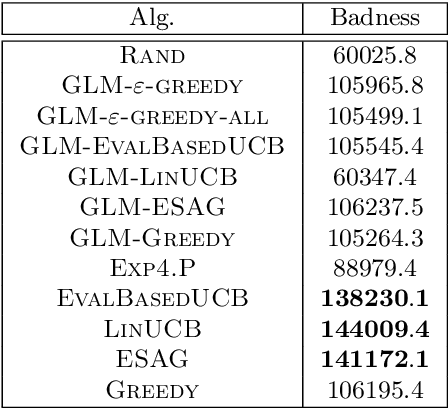
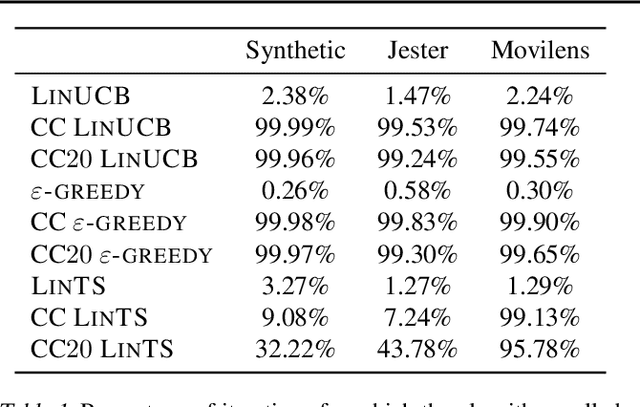
In many fields such as digital marketing, healthcare, finance, and robotics, it is common to have a well-tested and reliable baseline policy running in production (e.g., a recommender system). Nonetheless, the baseline policy is often suboptimal. In this case, it is desirable to deploy online learning algorithms (e.g., a multi-armed bandit algorithm) that interact with the system to learn a better/optimal policy under the constraint that during the learning process the performance is almost never worse than the performance of the baseline itself. In this paper, we study the conservative learning problem in the contextual linear bandit setting and introduce a novel algorithm, the Conservative Constrained LinUCB (CLUCB2). We derive regret bounds for CLUCB2 that match existing results and empirically show that it outperforms state-of-the-art conservative bandit algorithms in a number of synthetic and real-world problems. Finally, we consider a more realistic constraint where the performance is verified only at predefined checkpoints (instead of at every step) and show how this relaxed constraint favorably impacts the regret and empirical performance of CLUCB2.